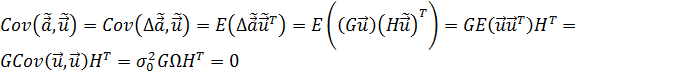Пусть имеется выборка
значений переменных x и y модели
Данная выборка получена на этапе наблюдения и предназначена для оценивания параметров модели
В рамках данной модели величины (*) связаны следующей СЛОУ:
Она называется системой уравнений наблюдения объекта в рамках исследуемой линейной модели, или иначе – схемой Гаусса-Маркова. Вот компактная запись этой схемы 
.
где 
- вектор известных значений эндогенной переменной yt модели;
- вектор неизвестных значений случайных возмущений ut;
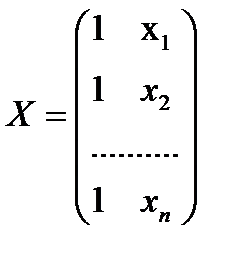- матрица известных значений предопределенной переменной x исходной модели, расширенная столбцом единиц (при наличии a0);
Наконец, 
– вектор неизвестных коэффициентов уравнения модели.
Оценку вектора обозначим 
. Тот факт, что эта оценка вычисляется по выборочным данным при помощи некоторой статистической процедуры, отразим: 
где f (·, ·) – символ процедуры.
Данная процедура именуется линейной относительно вектора 
значений эндогенной переменной yt, если: 
.
, где матрица коэффициентов, зависящих только от выборочных значений X предопределенной переменной хt.
Класс таких всевозможных линейных процедур оценивания по исходной выборке вектора 
обозначим символом F.
Наилучшая процедура f* (·, ·) из выбранного класса процедур F должна генерировать оценку 
, которая обладает одновременно двумя свойствами: ожидаемая оценка параметра совпадает с истинным значением
, i=0,1 (эффективности).
29.Свойства МНК-оценок параметров линейной модели множественной регрессии (ЛММР) при нормальном векторе случайных остатков: независимость случайных векторов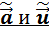 
Рассмотрим с учётом схемы Гаусса-Маркова в компактной форме и 
случайный вектор истинной ошибки
оценки 
(1)
или в компактном виде 
Видно, что вектор 
является выходом линейного преобразования вектора 
. Следовательно, вектор 
имеет нормальный закон распределения с числовыми характеристиками
.
Значит, и вектор 
является нормально распределённым случайным вектором с числовыми характеристиками 
.
Теперь рассмотрим вектор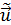 
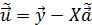
Подставим в это выражение (1) 
(2)
или в компактной записи 
Согласно (2) вектор 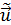тоже является выходом линейного преобразования вектора . Следовательно, и вектор 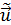имеет нормальный закон распределения. Его числовые характеристики
Для доказательства независимости нормально распределенных случайных величин 
необходимо и достаточно доказать, что эти векторы некоррелированны, т.е. что их взаимная ковариационная матрица нулевая: 
