Пусть 
- две независимые случайные переменные, имеющие 
распределение с числом степеней свободы n и m.
Случайная переменная 
называется дробью Фишера. Это позволяет при любом альфа вычислить 
, удовлетворяющее уравнению
, также называется Fкрит уровня 
, это (1-α)-квантиль распределения Фишера с числом степеней свободы n,m. 
Эту величины также можно вычислить в Excel, используя функцию FРАСПОБР по аргументам 
.
12. Случайный вектор и его основные количественные характеристики (на примере вектора 
левых частей схемы Гаусса – Маркова при гомоскедастичном неавтокоррелированном остатке).
Рассмотрим набор случайных переменных 
. Этот упорядоченный набор называется случайным вектором и обозначается 
:
(1)
Его основными характеристиками служат:
1) Вектор ожидаемых значений компонент:
так называют вектор констант, компоненты которого – мат. ожидания компонент вектора 
.
2) Ковариационная матрица:
(2)
По главной диагонали располагаются дисперсии компонент случайного вектора. Недиагональные элементы это ковариации компонентов. Например, 
- это дисперсия компоненты 
вектора (1). Элемент 
- это ковариация компонент 
и 
вектора (1) Матрица является симметричной.
Количественные характеристики
Свойство операции вычисления ожидаемого значения вектора.
Если обобщить свойство 
на аффинное преобразование случайного вектора 
в случайный вектор 
Свойство операции вычисления ковариационной матрицы случайного вектора.
Если же обобщить свойство 
на аффинное преобразование случайного вектора в случайный вектор 
.
Основные количественные характеристики выхода аффинного преобразования случайного вектора (на примере вектора мнк – оценок коэффициентов линейной модели при гомоскедастичном неавтокоррелированном остатке).
Рассмотрим набор случайных переменных 
. Этот упорядоченный набор называется случайным вектором и обозначается :
(1)
Его основными характеристиками служат:
3) Вектор ожидаемых значений компонент:
так называют вектор констант, компоненты которого – мат. ожидания компонент вектора 
.
4) Ковариационная матрица:
(2)
По главной диагонали располагаются дисперсии компонент случайного вектора. Недиагональные элементы это ковариации компонентов. Например, 
- это дисперсия компоненты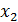 
вектора (1). Элемент 
- это ковариация компонент 
и 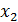вектора (1) Матрица является симметричной.
Количественные характеристики
Свойство операции вычисления ожидаемого значения вектора.
Если обобщить свойство на аффинное преобразование случайного вектора в случайный вектор
