Эта ошибка эквивалента по последствиям и симптомам неверному выбору типа регрессии. Пусть линейная регрессионная модель (1)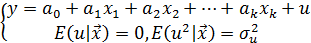 
со значениями параметров (2) 
адекватно описывает некоторый экономический объект в ситуации, когда значения объясняющих переменных 
принадлежат подмножеству 
(кратно 
области 
изменения . Однако если 
, где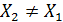 
, то адекватными объекту оказываются иные значения параметров модели (1), а именно (3): 
.
Экономист, не зная данного обстоятельства, оценивает модель (1) по выборке 
, где 
, и далее необоснованно использует оцененную модель для прогноза значений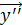 
эндогенной переменной в ситуации, когда 
(4). Очевидно, такие прогнозы могут оказаться недопустимо далекими от реальности, поскольку в правиле прогноза (4) оценки коэффициентов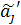 
оказываются смещенными: 
.
Диагностика данной ошибки приводит к задаче построения теста совпадения значений (2) и (3) параметров модели (1). Тест Чоу базируется на предположении, что случайный остаток в линейной регрессионной модели (1) нормально распределен, гомоскедастичен и не имеет автокорреляции. Далее в рамках модели (1) при данном предположении о случайном остатке получены две выборки: , 
объемов соответственно 
, и имеется основание для подозрений, что выборке соответствуют одни значения параметров модели (2), а выборке 
- другие значения (3). Добавим, что если справедлива гипотеза (5) 
, то выборки , можно объединить в одну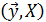 
, где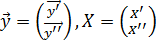 
, и по ней оценивать единые параметры 
модели (1). Однако, когда справедлива альтернативная гипотеза (6) 
, то объединять эти выборки нельзя.
Тест Чоу - это формализированная процедура проверки гипотезы (5) против альтернативы (6), состоящая из следующих шагов.
Шаг 1. Модель (1) оценивается МНК по выборке объема 
При справедливой гипотезе (5) и отмеченном выше предположении о случайном остатке справедливо соотношение: 
.
Шаг 2. Модель (1) оценивается МНК по выборке 
объема 
. При справедливой гипотезе (5) имеет соотношение 
, причем отсутствие автокорреляции случайного остатка обеспечивает независимость случайных переменных 
и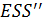 
. Следовательно, 
Шаг 3. Модель (1) оценивается по объединенной выборке объема 
При справедливой гипотезе (5) 
. Случайная переменная 
распределена по закону Фишера с количествами степеней свободы 
. Переменная 
может служить статистикой критерия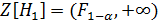 
гипотезы (5) против альтернативы (6). Символом 
обозначена квантиль уровня (
распределения Фишера с количествами степеней свободы .
Шаг 4. Проверяется справедливость неравенства 
. Если оно справедливо, то гипотеза (5) принимается. Если же неравенство несправедливо, то принимается гипотеза (6), и параметры модели (1) интерпретируются как различные для двух выборок.
