Ряд 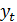 именуется стационарным, если его ожидаемое значение и дисперсия постоянны (не зависят от переменной времени t), а автоковариационная и автокорреляционная функции являются четными функциями одного аргумента
именуется стационарным, если его ожидаемое значение и дисперсия постоянны (не зависят от переменной времени t), а автоковариационная и автокорреляционная функции являются четными функциями одного аргумента  :
:
1) 
2) 
3) 
4) 
Ряд 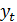 именуется нестационарным, если хотя бы одно условие 1-4 не выполняется.
именуется нестационарным, если хотя бы одно условие 1-4 не выполняется.
основные характеристики временного ряда:
1) Математической ожидание ряда 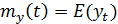
2) Дисперсия временного ряда 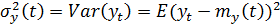
3) Автоковариационная функция ряда
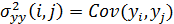 – функция двух аргументов
– функция двух аргументов 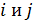 при перестановке которых значения функций не меняются.
при перестановке которых значения функций не меняются.
4) Автокорреляционная функция ряда

Оценки этих характеристик могут быть найдены по одной реализации этого ряда
1) Оценка математического ожидания:

2) Оценка дисперсии:
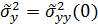
3) Оценка автоковариационной функции:

4) Оценка автокорреляционной функции:

50. Частная автокорреляционная функция стационарного временного ряда и алгоритм её оценивания.
Рассмотрим уровни ряда ut на отрезке [t;t+ τ] (ut, ut+1, …, ut+ τ -1, ut+ τ)
Удалим(при помощи уравнения регрессии) влияние членов ut, …, ut+ τ-1 из уровней ut и ut+ τ. После этого рассмотрим ковариацию остатков ut и ut+ τ. Это и будет частная автокорреляционная функция в точке τ.
Ϭuu(p)(τ)=  (2.10)
(2.10)
На основании 2.10 дается определение частной автокорреляционной функции стационарного ряда
ρuu(p)(τ)= 
Частная автокорреляционная функция белого шума имеет уравнение
ρξξ(p)(τ)= ρξξ(τ)= 
Можно обосновать следующий алгоритм оценивания частной автокорреляционной функции ряда по его реализации:
Оценить МНК параметры модели
1. 
2. Принять
оценкой ρuu(p)(τ) оценку βτ.
51. Модель AR(p) и её идентификация.
Авторегрессия первого порядка:

 ,
,  ,имеет смысл коэффициента корреляции уровней ряда в соседние моменты времени.
,имеет смысл коэффициента корреляции уровней ряда в соседние моменты времени.
Автокорреляционная функция имеет уровни ρuu(i,j)=ρ|i-j|=ρτ и экспоненциально убывает с ростом лага τ
При ρ=0 ряд превращается в WN. Если ρ=1, то ряд становится нестационарным рядом, называющимся случайным блужданием.
Теорема позволяющая идентифицировать временной ряд AR(1):
Если utϵAR(1), то его частная автокорреляционная функция тождественно равна 0, при τ>1
ρuu(p)(τ)= 
Модель авторегрессии порядка р задается поведенческим уравнением:
ut=β1ut-1+ β2ut-2+…+ βput-p+ξt
Для модели AR(p) частная автокорреляционная функция авна 0 при  .
.
52. Модель MA(q) и её идентификация.
Модель первого порядка:

Теорема. Если utϵMA(1) то
1) Ряд порожденный этой моделью является стационарным
2) E(ut)=0, Ϭu2=Ϭξ2(1+γ2)
3) Автокорреляционная функция ряда MA(1) имеет уравнение:
ρuu(τ)= 
Рекурсивное уравнение модели:
ut=γ1ξt-1+ γ 2ξt-2+…+ γ pξt-p+ξt
Теорема. Если utϵMA(q) то ρuu(τ)=0 при τ>q.
53. Оптимальный линейный алгоритм прогнозирования уровней стационарного временного ряда.
Пусть уровни ряда ut  STS наблюдались в моменты времени t=1,2,…,n. Результаты этих наблюдений обозначим символами u1, u2,…,un. Расположим эти результаты в обратном порядке и будем интерпретировать такой набор как случайный вектор
STS наблюдались в моменты времени t=1,2,…,n. Результаты этих наблюдений обозначим символами u1, u2,…,un. Расположим эти результаты в обратном порядке и будем интерпретировать такой набор как случайный вектор  , т.е.
, т.е.
 T=(un,..,u2,u1) (1).
T=(un,..,u2,u1) (1).
Задача прогнозирования заключается в построении правила прогноза будущего уровня  n+τ наблюдаемого ряда по его известным уровням (1), следовательно
n+τ наблюдаемого ряда по его известным уровням (1), следовательно  n+τ есть значение некоторой функции f наблюдаемых уровней (1):
n+τ есть значение некоторой функции f наблюдаемых уровней (1):
 n+τ =f (u1, u2,…,un). (2)
n+τ =f (u1, u2,…,un). (2)
Прогноз будет являться оптимальным, если он удовлетворяет требованиям, предъявляемым к статистическим процедурам:
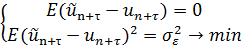 (3)
(3)
Прогнозный алгоритм оптимальный в множестве всех функций аргумента- это условное математическое ожидание:
 u1, u2,…,un). (4)
u1, u2,…,un). (4)
Пусть временной ряд ut  STS является гауссовским, т.е. его уровни образуют нормально распределенный случайный вектор
STS является гауссовским, т.е. его уровни образуют нормально распределенный случайный вектор
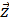 T =(u1, u2,…,un,…,ut+τ,…,uN). (5)
T =(u1, u2,…,un,…,ut+τ,…,uN). (5)
Вектор наблюдений (1) роль объясняющего вектора  , поэтому
, поэтому
 (6)
(6)
Здесь  Будущий уровень ряда
Будущий уровень ряда  n+τ интерпретируем как вектор
n+τ интерпретируем как вектор  . Так что
. Так что 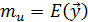 .
.
Ковариационная матрица  . Находим матрицу
. Находим матрицу  =
=  T.
T.
Тогда оптимальный алгоритм прогнозирования уровней гауссовского стационарного временного ряда принимает вид
 u1, u2,…,un)=
u1, u2,…,un)= 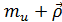 T
T  (7)
(7)
Алгоритм (7) является линейным. Действительно, проведя перегруппировку членов в правой части равенства (7), увидим, что
 a0+a1un+a2un-1+…+anu1.
a0+a1un+a2un-1+…+anu1.
54. Модели нестационарных временных рядов. Идентификация модели тренда.
a) Аддитивная модель временного ряда имеет следующую спецификацию
 (1)
(1)
Алгоритм выбора тренда T(t) в модели (1):
1. Наблюдаем уровни ряда yt, для которого создаем модель (1)
2. Из наблюдаемых уровней отбираем уровни базовых периодов. Пусть отобрано m уровней базовых периодов: y1, y2,…,ym. (2)
3. Вычисляем по уровням (2) при τ=1,2,…,m-1 разности Δyτ=yτ+1-yτ
4. Задаваясь значениями τ=1,2,… и Δτ=1, вычисляем значения индикаторов функции тренда:
I1(τ)=Δ(2)yτ=Δyτ+1-Δyτ
I2(τ)= Δ(3)yτ=ΔI1(τ)=I1(τ+1)-I1(τ)
I3(τ)=Δ( )=
)= 
I4(τ)=Δ(
I5(τ)=Δ(τΔyτ)=(τ+1)Δyτ+1-τΔyτ
I6(τ)=Δ(2)(
5. Отмечаем те индикаторы, значения которых в ответ на изменение переменной τ, колеблются вокруг нуля. По данному индикатору выбираем соответствующую функцию тренда T(t) (наиболее простую):
- для I1- линейная
-для I2-парабола второго порядка
- для I3-показательная
- для I4-степенная
- для I5-логарифмическая
- для I6- логистическая
b) Модель броуновского движения

Временной ряд yt обладает следующими характеристиками
my(t)=y0, σy2=σξ2t, σyy(I,j)= σξ2min(I,j)
55. Оценивание линейной модели с автокоррелированным остатком AR(1) алгоритмом Хильдретта – Лу.
Модель AR(1) имеет следующую спецификацию:




t, t-1 
уравнение модели запишем в идее: 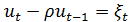
1. Задаемся на промежутке [0,1) набором пробных значений  по правилу
по правилу
 (1)
(1)
где N-некоторое натуральное число
2. При каждом значении (1) составляем систему уравнений наблюдений



И вычислим на основании этой системы МНК-оценки  ,
, 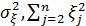
3. Выбираем из множества пробных значений (1) такую величину  , при которой имеет место экстремум
, при которой имеет место экстремум  .
.
Выбранные величины и будут искомыми оценками параметров модели AR(1)
56. Проблема мультиколлинеарности, типы и симптомы мультиколлинеарности. Методика отбора регрессоров в линейной модели в ситуации мультиколлинеарности.
Мультиколлинеарность- ситуация, в которой в уравнениях наблюдений столбцы матрицы X становятся практически линейно зависимыми, что входит в противоречии с исходной предпосылкой теоремы Гаусса-Маркова. В ситуации мультиколлинеарности оценки параметров линейной регрессионной модели становятся ненадежными.
В условиях мультиколлинеарности текущий уровень ряда, как правило, может быть во многом объяснен предыдущими значениями
xt≈c0+c1xt-1+c2xt-2 (1)
Если (1) превращается в точное равенство, возникает ситуация совершенной мультиколлинеарности.
Симптомы:
а) резкое изменение значений оценок модели при незначительной вариации состава обучающей выборки;
б) наличие в оцененной модели небольших по модулю значений  при достаточно высоком значении коэф-та детерминации;
при достаточно высоком значении коэф-та детерминации;
в) большое значение коэф-та детерминации между каждой объясняющей пер-ой линейной модели и ее остальными объясняющими пер-ми.






