В регрессионном анализе изучается односторонняя зависимость переменной Y от одной или нескольких переменных Х1 …., Хk. Основная задача регрессионного анализа – установление формы зависимости между зависимой (Y) и независимыми (Х1 …., Хk) переменными и анализ достоверности параметров этой зависимости. Такие переменные, как расходы на рекламу, транспорт, численность населения и т.п. являются независимыми переменными, а те переменные, которые мы пытаемся оценить (например, объем продаж), являются зависимыми переменными.
Схема составления прогноза заключается в сборе данных о значениях зависимых и независимых переменных, их анализе на предмет наличия связи (корреляция) и выведении математического уравнения, описывающего эту связь (регрессия).
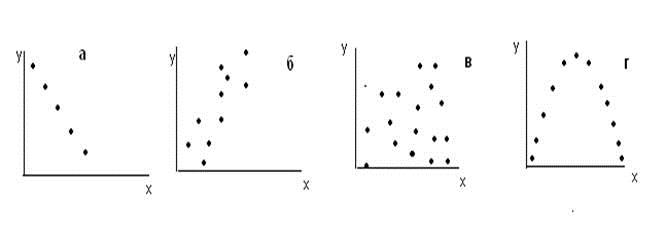
Первая стадия корреляционного анализа – сбор данных о значениях переменных и составления точечных диаграмм (ХY-диаграммы). Точечные диаграммы имеют различный вид:
Так, на рис. а пример абсолютной отрицательной корреляции, на рис. б – сильной положительной корреляции. На рис. в – взаимосвязь между значениями не усматривается, на рис. г взаимосвязь наличествует, но это не линейная зависимость, а параболическая.
Предположение наличия линейной зависимости между двумя переменными основывается на значении коэффициента корреляции r, который рассчитывается по формуле:
, (1.1)
где n – число пар значений переменных, а Σ символ суммирования.
Значение коэффициента корреляции колеблется от -1 (в случае абсолютной отрицательной корреляции) до +1 (в случае абсолютной положительной корреляции). Такие диаграммы как показаны на рис. в, г, дадут коэффициенты корреляции почти равные нулю. Хотя на рис. г точки взаимосвязаны между собой, но там зависимость параболическая, а коэффициент корреляции измеряет тесноту линейной связи. Это свидетельствует о важности не только расчетов, но и рассмотрения точечной диаграммы, поскольку даже при r близким к нулю возможно тесная взаимосвязь, но не линейная, а, например, параболическая как показано на рис. г.
Если установлена тесная линейная корреляция между переменными, то можно вывести уравнение прямой и использовать её для прогнозирования поведения зависимой переменной в будущем. Этот процесс носит название ЛИНЕЙНОЙ РЕГРЕССИИ.
Уравнение прямой (линейной) регрессии имеет общий вид:
Y = a + b*x,
где y – результативный показатель; х – независимая переменная (фактор); a и b представляют собой константы, их значения определяют положение и направленность прямой в осях координат.
Константа а называется точкой пересечения прямой с осью ординат и её значениепредставляет собой значение у, когда х =0. Константу b называют коэффициентом при х.
Задача регрессионного анализа заключается в экспериментальном определении коэффициентов регрессии, путем наблюдения за характером изменения входных параметров (факторов) и выходной величины (результативного показателя). Линейная модель уравнения регрессии строится по методу наименьших квадратов. Этот критерий минимизирует сумму квадратов вертикальных отклонений точек от прямой регрессии.
В реальных процессах зависимость результативного показателя у зависит от целого ряда переменных (факторов) х1, х2, …,хk. – и это будет множественная регрессия. Модель множественной регрессии имеет следующий вид:
(1.2)
j ≠ i,
где bi – линейные коэффициенты, bii – нелинейные коэффициенты, bij- коэффициенты, учитывающие взаимное влияние факторов.
Для анализа общего качества регрессии используют коэффициент детерминации (определенности) R2. Он характеризует долю вариации (разброса) зависимой переменной, объясненной с помощью данного уравнения. Т.е. с увеличением объясняемой доли разброса R2 à 1.
Значимость уравнения регрессии определяют, используя критерий Фишера (F-критерий). Расчетное значение Fв сравнивается с критическим значением (Fкр), определяемого по таблице критических точек распределения Фишера: Fкр = k/n–k – 1; где k - число факторов, (n-k-1) – число степеней свободы знаменателя и n – это число параллельных опытов. Если Fв > Fкр - то полученное уравнение регрессии значимо, т.е. хотя бы один из коэффициентов уравнения не равен нулю.
Значимость коэффициентов регрессии проверяется с помощью t-критерия, основанного на распределении Стьюдента. Если вычисленный t-критерий коэффициента bi (çtbi ê) больше tкр., то коэффициент значимый и влияние соответствующего фактора значимо. tкр определяют по уровню значимости и числу степеней свободы f = n-k-1.
33. Решение проблемы спецификации через подбор формы модели.
Проблема спецификации модели
Эта проблема по существу решается на первых трех этапах моделирования (1-й этап (постановочный) — определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли;
2-й этап (априорный) — предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации, в частности, относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих;
3-й этап (параметризация) — собственно моделирование, т.е. выбор общего вида модели, в том числе состава и формы, входящих в нее связей;)
и включает в себя:
1. определение конечных целей моделирования (прогноз, имитация различных сценариев социально-экономического развития анализируемой системы, управление);
2. определение списка экзогенных и эндогенных переменных;
3. определение состава анализируемой системы уравнений и тождеств, их структуры и соответственно списка предопределенных переменных;
4. формулировку исходных предпосылок и априорных ограничений относительно:
o стохастической природы остатков (в классических вариантах моделей п ос тулируются их взаимная статистическая независимость или некоррелированность, нулевые значения их средних величин и, иногда, сохранение постоянными в процессе наблюдения значений их дисперсий — гомоскедастичностъ);
o числовых значений отдельных элементов матриц коэффициентов в модели;
o поведение некоторых эндогенных переменных.
Итак, спецификация модели — это первый и, быть может, важнейший шаг эконометрического исследования. От того, насколько удачно решена проблема спецификации и, в частности, насколько реалистичны наши решения и предположения относительно состава эндогенных, экзогенных и предопределенных переменных, структуры самой системы уравнений и тождеств, стохастической природы случайных остатков и конкретных числовых значений части элементов матриц коэффициентов, решающим образом зависит успех всего эконометрического моделирования
Спецификацией переменных называется процесс отбора наиболее важных факторных переменных при построении модели регрессии.
Если в процессе эконометрического моделирования была осуществлена неправильная спецификация переменных, то это может привести к негативным последствиям, среди которых особо можно выделить два пункта:
1) из модели регрессии могут быть исключены факторные переменные, оказывающие наибольшее влияние на результативную переменную;
2) в модель регрессии могут быть включены факторные переменные, практические не связанные с результативной переменной или оказывающие на неё незначительное воздействие.
Предположим, что на основе собранных данных была построена нормальная модель множественной регрессии вида:
Y=Xβ+ε(1)
Данную модель можно рассматривать как базисную или ограниченную модель регрессии между исследуемыми переменными.
Тогда неограниченная модель данной регрессионной зависимости будет иметь вид:
Y=Xβ+Zλ+ε(2)
где Y – вектор результативных переменных;
X – вектор количественных факторных переменных;
Z – некоторая фиктивная переменная;
Β, λ – вектор неизвестных коэффициентов модели регрессии без ограничений, подлежащих оцениванию.
Рассмотрим случай исключения факторных переменных, оказывающих наибольшее влияние на результативную переменную, из модели регрессии.
Предположим, что модель регрессии с ограничениями является значимой. Исходя из этого условия, рассчитаем оценку коэффициента β, полученную методом наименьших квадратов, в оцениваемой модели регрессии с ограничениями (1):
Подставим в данную формулу вместо Y выражение Xβ+Zλ+ε:
Охарактеризуем полученную оценку коэффициента β модели регрессии с ограничениями с точки зрения свойства несмещённости. Для этого рассчитаем математическое ожидание оценки
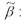
где BIAS – это смещение оценки коэффициента β.
Таким образом, оценка 
является смещённой, и устранить эту смещённость невозможно, даже при условии увеличения объёма выборочной совокупности.
Оценка коэффициента β модели регрессии с ограничениями (1) будет обладать свойством несмещённости в двух случаях:
1) если коэффициент при фиктивной переменной Z будет равен нулю:
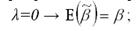
2) при условии, что пропущенные переменные будут ортогонально включены в модель:
XTZ = 0.
Рассчитаем ковариацию оценки коэффициента β модели регрессии с ограничениями (1):
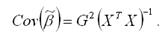
Матрица ковариаций МНК-оценок принимает такой вид только в том случае, если модель (1) является значимой.
Рассмотрим случай, когда в модель регрессии могут быть включены факторные переменные, практические не связанные с результативной переменной или оказывающие на неё незначительное воздействие.
Предположим, что модель регрессии без ограничений (2) является значимой. Исходя из этого условия, оценим коэффициенты модели регрессии с ограничениями (1).
Представим регрессионную модель с ограничениями (1) в следующем виде:
Пусть W – это переменные (X,Z) модели регрессии. Тогда оценка коэффициента β модели регрессии без ограничений может быть записана следующим образом:
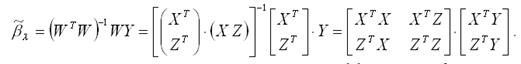
Охарактеризуем полученную оценку коэффициента β модели регрессии без ограничений с точки зрения свойства несмещённости. Для этого рассчитаем математическое ожидание оценки
Следовательно, оценка 
является несмещённой оценкой коэффициента регрессии β модели (2). Если в данную модель включить один дополнительный фактор, то оценки уже включённых факторных переменных свойства несмещённости не утратят. Но если в модель регрессии будут включены много лишних параметров, то точность оценок будет падать.
Матрица ковариаций МНК-оценок модели регрессии без ограничений будет иметь вид:
Матрица ковариаций будет иметь такой вид только в случае значимости модели регрессии без ограничений.
