Рассмотрим линейную модель множественной регрессии:
.
По выборке объёма n оценивается уравнение регрессии
,
где неизвестные коэффициенты оцениваются МНК, при котором минимизируется сумма квадратов остатков, позволяя получить систему нормальных уравнений:
Решение системы может быть получено, например, по формулам Крамера:
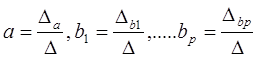, при этом
.
Оценим коэффициенты регрессии МНК в матричной форме. Обозначим
, 
, 
, 
, 
Значения признака Матрица объясняющих Вектор Вектор Вектор
переменных, столбцами регрессора j случайных коэффициентов
которой являются Xj ошибок регрессии
1 7. Допущения применения метода наименьших квадратов. Условия Гаусса-Маркова.
1) Математическая форма зависимости эндогенных переменных от экзогенных переменных модели носит линейный характер (другие типы уравнений, отражающих зависимость значения одной переменной от других, должны быть приведены к линейному виду, прежде чем возможно будет использовать метод наименьших квадратов), и независимые переменные модели являются единственными значимыми факторами, определяющими поведение зависимой переменной;
2) Значение ошибки ε нормально распределено со средней, равной 0, и постоянной дисперсией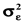 
, 
. То есть, хотя значение переменной Y значимо определяется только учтенными в модели факторными признаками, существует также ряд второстепенных факторов, некоторые из которых будут положительно влиять на величину Y, некоторые – отрицательно. В случае множества как положительных, так и отрицательных влияний значение ошибки ε будет нормально распределено. Нормальное распределение полностью определяется двумя параметрами: средней и средним квадратическим отклонением (дисперсией σ2). Чем больше случайных величин действует вместе, тем точнее проявляется закон нормального распределения. Допущение о постоянной дисперсии говорит о постоянности разброса значений ε, вне зависимости от величины значения факторов. Тогда значение ошибки обладает свойством гомоскедастичности. Если разброс значений ошибки ε непостоянен, то имеет место явление гетероскедастичности.
3) Последующие значения ошибок независимы друг от друга, то есть ковариация в парах значений ε равна нулю (covε iεj = 0). Это означает, что второстепенные факторы или факторы-причины ошибки для одной из величин Y, не приводят автоматически к ошибкам для всех наблюдений Y. Когда значения ε независимы, то данные неавтокоррелированы. Если же значения ε не являются независимыми, то данные демонстрируют наличие автокорреляции.
4) Независимые переменные являются нестохастическими, то есть их значения для модели детерминированы, заданы изначально.
2) Условие Гаусса-Маркова.Для сущ-ия классической модели регрессии необходимо выполнение усл-ий Гаусса-Маркова. Традиционно называют четыре усл-ия, пятая явл-ся дополнением:
1. Матем ожидание СВ U = 0, то есть M(ui) = 0. Это означает, что колебания неопр-сти будут взаимопогашаться.
2. CВ U имеет постоянную дисперсию. В частности в простейших случаях предполагается ее равенсто единице. 
.
3. Значения фактора неопр-сти, измеренные в различные моменты времени не коррелированы.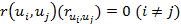 
.
4. Наблюдается обязательное влияние фактора неопр-сти на результат.
5. Предполагается нормальное распределение СВ U.
18. Проверка оценок параметров линейной регрессии. Определение оценок параметров регрессии с помощью функции ЛИНЕЙ Н.
Проверка адекватности моделей, построенных на основе уравнений регрессии, начинается с проверки значимости каждого коэффициента регрессии. Значимость коэффициента регрессии осуществляется с помощью t-критерия Стьюдента (отношение коэффициента регрессии к его средней ошибке):
.
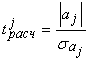Коэффициент регрессии считается статистически значимым, если 
превышает tтабл - табличное (теоретическое) значение t-критерия Стьюдента.
Проверка адекватности всей модели осуществляется с помощью F -критерия и величины средней ошибки аппроксимации 
.
Значение средней ошибки аппроксимации, определяемой по формуле
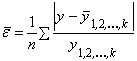не должно превышать 12 - 15 %.
Расчетное значение F -критерия определяется по формуле и сравнивается с табличным:
, где 
- коэффициент множественной детерминации.
Если F расч> F табл, связь признается существенной.
