СОА показывает среднее отклонение расчетных данных результативного признака от фактических. Допустимый предел 8-10%.
Величина отклонений фактических и расчетных значений результативного признака 
по каждому наблюдению представляет собой ошибку аппроксимации.
Поскольку 
может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
Отклонения можно рассматривать как аб с олютную ошибку аппроксимации, а 
- как относительную ошибку аппроксимации
Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению определяют среднюю ошибку аппроксимации: 
Возможно и иное определение средней ошибки аппроксимации: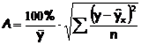 
Если А =10-12%, то можно говорить о хорошем качестве модели.
Смысл средней ошибки аппроксимации в том, что это один из многих способов оценить разницу между аппроксимированнм и реальным значениями изучаемой величины. То есть это "квантификатор" потерь (в экономическом смысле) или риска.
27) Эластичность в социально-экономических моделях. Частные коэффициенты эластичности. Практическое применение.
Эластичность — мера чувствительности одной переменной (например: спроса или предложения) к изменению другой (например: цены, дохода), показывающая, на сколько процентов изменится первый показатель при изменении второго на 1 %.
Внимание отдельных факторов в многофакторных моделях может быть охарактеризовано с помощью частных коэффициентов эластичности, которые в случае двухфакторной модели вычисляются по формулам:
Частные коэффициенты эластичности показывают, на сколько процентов измениться результирующий признак, если значение одного из факторных признаков измениться на 1%, а значение другого факторного признака останется не низменным.
В экономических исследованиях широкое применение находит такой показатель, как коэффициент эластичности. Если зависимость между переменными x и y имеет вид y=f(x), то коэффициент эластичности Э вычисляется по формуле
Коэффициент эластичности Э показывает, на сколько процентов в среднем изменится результативный признак у при изменении фактора х на 1 % от своего номинального значения. Для линейной регрессии коэффициент эластичности равен
28. t-критерий Стьюдента. Алгоритм выполнения. Практическое применение.
t – критерий Стьюдента проводится с целью проверки значимости каждого параметра в отдельности.
Если проверяется значимость каждого параметра, то выбирают t – критерий Стьюдента и гипотеза строится 
… и все остальные параметры при факторе проверяются на = 0 по отдельности.
Алгоритм t – критерия:
1) Выдвигается H0 и H1 гипотезы, рассчитываются значения статистики, лежащей в основе критерия и дающей ему название – t-статистика.
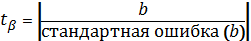
Сконфигурировав линейнуб ф-ию (вызвав «линейн») и вызвав предварительно выбранный диапазон ячеек (2x5) статистику (в поле «статистика» = 1), стандартная ошибка соответствующего коэф-та находится под ним:
| b | A |
| СО (b) | СО (а) |
2) Из таблицы t-распределения с заданным уровнем значимости, кот задает № столбца и числом степеней свободы, рассчитанному на основе числа наблюдений № - кол-во оцениваемых параметров задает № строки, выбирается t-табличное.
| Число степеней свободы Уровни значимости | 1% | 5% | 10% |
| … | |||
| t 1% | t 5% |
N=10; Число степеней свободы = 8. Уровень значимости всегда берется по двустороннему критерию.
3) Сравниваем 
с каждым из табличных значений:
Следовательно, делается вывод о статистической значимости.
28. F-критерий Фишера. Алгоритм выполнения. Практическое применение.
F-критерий Фишера проводится с целью проверки значимости всей модели в целом.
Алгоритм F– критерия:
1) При выдвижении Н0 сравниваются (строятся отношения) дисперсий (Дфак – факторной и Дост – остаточной). И на основе их соотношения рассчитывается F-статистика:
F-статистика – величина, лежащая в основе критерия и дающая ему название.
Дисперсия рассчитывается в рамках дисперсионного анализа (см далее).
ЛИНЕЙН
| B | A |
| СО (b) | СО (a) |
| R2 | СО (y) |
| F-статистика | ЧСС |
|
СО – стандартная ошибка
В нулевой гипотезе (Н0) делается предположение о равенстве дисперсии факторной и дисперсии остаточной.
H0: Дф = Дост
H1: Дф 
Дост
В случае, если удастся принять альтернативную гипотезу дополнительно делается сравнение дисперсии через неравенства: Дф 
Дост (делается дополнительно через дисперсионный анализ).
2) Из таблиц F-распределения выбираются критические (табличные) значения F -статистики. Таблица сформирована с учетом:
1. Уровня значимости (в заголовке таблицы);
2. Числа степеней свободы – ЧСС (равно номеру строки, номер строки в таблице F-критерий, t-критерий), для парной модели ЧСС = n -2 (n – число наблюдений);
3. Кол-во независимых переменных – НП (номер столбца).
F-распределение 1%
| Кол-во НП ЧСС | |
| = n-2 | |
Число степеней свободы рассчитывается в общем виде по формуле:
ЧСС = n-k-1, k – кол-во независимых переменных
3) Выполняется сравнение F-статистики из п. 1 с F-критическими из п. 2 (2 при 1%, и 5%).
Для отклонения нулевой гипотезы требуется выполнение неравенства:
В противном случае делается вывод о статистической значимости уравнения регрессии в целом.
Дисперсионный анализ
В дисперсионном анализе и в F-критерии Фишера рассматривают условно сконструированные дисперсии на основе соответствующих сумм квадратов. В основе лежит равенство (**) – разложение общей суммы квадратов отклонений СВ от среднего на факторную и остаточную сумму квадратов.
Для перехода к дисперсиям соответствующая сумма квадрата делится на ЧСС (свое для каждой суммы).
Пример
Определить ЧСС для расчета среднего значения СВ y, имеющей 5 значений.
| yi | Y1 | y2 | y3 | y4 | y5 |
| |||||
| -2 | -1 |
n = 5, ЧСС = 4
Доверительные интервалы
а - СО (а)* t табл 1% <= альфа<=а+ СО(а)* t табл 1%
b + СО(b) * t табл 5% <= бетта <= b + СО (b) * t табл 5 %
29. Взаимосвязь между t-критерием, F-критерием и коэффициентом детерминации R2.
Для линейной парной модели выполняется след связь между F и t критериями:
Таким образом, говорят о равносильности в данном частном случае этих двух критериев на практике.
В ряде прикладных программ и задач требуется оценить значимость коэффициента корреляции. Для этого строится гипотеза:
Н0: r генерал = 0
H1: r генерал не равно 0
Проверка осуществляется на основе расчета t – статистики через выборочный коэф-т корреляции, а затем на основе таблиц t – распределения выполняется сравнение рассчитанного значения с табличным.
Для линейной парной модели r2 – это формула для расчета коэф-та детерминации: R2 = r2.
Чем ближе R2 к единице, тем лучше регрессия аппроксимирует эмпирические данные (приближает наблюдаемые данные).
Если R2 = 1, то эмпирические точки лежат на линии регрессии, и между экзогенной и эндогенной переменными сущ-ет лин функциональная зависимость.
Если R2 = 0, то изменение эндогенной переменной у всецело опр-ся изменением всех неучтенных в модели факторов (от изменения x не зависит).
| yi = | 
| + | 
| 
|
R2 = 0,3
|
1 – R2 = 0,7
|
В прикладных задачах всегда начинают исследование с линейной функции, затем берут либо степенную, либо показательную. Затем полином второй степени и в редком случае третьей.
