Для всех моделей необходимо рассчитать интервальную оценку для возможного значения эндогенной переменной.
Наиболее часто строятся 95% и 99% интервалы. Данные интервалы рассчитываются для t-критерия Стьюдента, исходя из статистических таблиц t-распределения по следующим формулам:
Для нахождения значений tтабл необходимо воспользоваться двусторонним тестом и взять соответствующее число степеней свободы (оно находится в общей таблице), на их пересечении и будет нужное нам значение.
Стандартные ошибки а и в также берем из таблицы.
Вот пример таблицы.
| b | 0,728324 | -0,57803 | a |
| c.o.b | 0,084875 | 0,579213 | c.o.a |
| R2 | 0,936416 | 0,596715 | c.o.(y) |
| F стат. | 73,63636 | ЧСС | |
| Σфакт | 26,21965 | 1,780347 | Σост |
Доверительные интрвалы
а - СО (а)* t табл 1% <= альфа<=а+ СО(а)* t табл 1%
b + СО(b) * t табл 5% <= бетта <= b + СО (b) * t табл 5 %
Доверительная вероятность задает условную ошибку, то есть, если вероятность - 95%, то ошибка – 5%; если вероятность – 99%, то ошибка – 1%.
Право на ошибку 5% (или 1%) называется уровнем значимости, поэтому вывод всегда делается с уровнем значимости
Интервальный прогноз заключается в построении доверительного интервала прогноза, т. е. нижней и верхней границ интервала, содержащего точную величину для прогнозного значения с заданной вероятностью.
При построении доверительного интервала прогноза используется стандартная ошибка прогноза.
21. Модели множественной регрессии. Схема построения.
В случае, если на эндогенную переменную влияют одновременно в момент i-го наблюдения более одного фактора, реальная модель с учетом аддитивной связи выглядит:
В случае получения коэф-тов регрессии (b, с, t…) вручную строят систему одновременных уравнений с соответствующим числом величин.
В случае расчета с помощью табличного процессора Exсel сущ-ет четкая закономерность получения коэф-тов регрессии – получения их в обратном порядке.
Фрагмент
В свободном месте раб области Excel резервируем кол-во ячеек, равное числу независимых переменных + 1 для a. А затем для выполнения соответствующих действий получаем искомые хар-ки.
| t | … | с | b | a |
ЛИНЕЙН (y;(z … t)) (1; 0) f2 + ctrl + shift + enter
| y | x | z | … | t |
Все данные, относящиеся к факторам, объединяются в Excel под названием x. Поэтому они всегда должны стоять рядом
Для тестов на компьтере:
1) Реальный разброс точек при МНК, построение линейной регрессии.
2) Автокорреляция в остатках (в них прослеживается какая-либо закономерность)
Модель множественной регрессии на практтике частично анализируется с помощью модели парной регрессии, однако дополняется некоторыми практически применимыми допущениями:
1. Модель линейная в множественной регрессии заменяется на парную линейную модель, но проверяется мультиколлинеарность объясняющих переменных
Мультиколлинеарность – это высокая взаимная коллинеарность объясняющих переменных. Она опр-ся расчетом коэф-том корреляции между объясняющими переменными (между x и y ее не будет). Высокая корреляция: 0,7 < r <1
Необходимо исключить из модели одну из пары с выделенной мультиколлинеарностью.
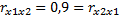
Исключают ту переменную, которая имеет менее слабую связь с объясняемой переменной (y).
| rпер | y | x1 | x2 | … | xm |
| y | |||||
| x1 | 0,9 | ||||
| x2 | 0,9 | ||||
| … | |||||
| xm |
ryy = 1, так как функциональная зависимость
2. Нелинейные множественные модели
В моделях множественной регрессии нецелесообразно заменять функцию кусочно-линейной. Проблема заключается в повышении точности кусочного представления. Если отдельные короткие участки исследуемой кривой представить не прямыми, а разложить в ряд Тейлора, тогда нелинейная модель получит точную замену.
3. Для всех моделей рассчитывают помимо обычного коэф-та детерминации скорректированный:
Cкорректированный в отличие от обычного коэф-та детерминации может быть меньше 0 (
).
Скорректированный коэф-т детерминации прихходится считать, так как в ММР однозначно происходит снижение ЧСС.
Пример
для (2) ЧСС = n – (m + 1)
(m + 1) = k
m – число независимых переменных
k – кол-во оцениваемых переменных
Экономиисты должны четко отслеживать целесообразность включения в модель объясняющих переменных (цена билета на аттракцион в зависимости от роста, веса и т д).
См 6 этапов эконометрического моделирования.
Коэф-т корреляции можно рассчитать как разность:
А скорректированный коэф-т детерминации рассчитывается с учетом корректировки на соответствующее ЧСС:
n – число наблюдений
k – кол-во оцениваемых параметров
4. Для всех моделей проверка качества и статистической значимости опр-ся аналогично моделям парной регрессии.
В Excel считаем R2 и F
0,02; 0,01; 0,05 – стандартные ошибки
| 
| |
| 0,7 | 0,3 | 0,4 |
| 0,05 | 0,01 | 0,02 |
| 
| СО(а) = 0,01 |
| 
| СО(b) = 0,3 |
| 
| 
|
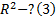
Для парной модели t-статистика высчитывается по коэф-ту регрессии b.
5. Для всех моделей требуется рассчитать интервальную оценку для возможного значения эндогенной переменной.
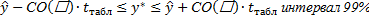
Множественная регрессия – уравнение связи с несколькими независимыми переменными:
где 
- зависимая переменная (результативный признак);
- независимые переменные (факторы).
Линейная модель множественной регрессии имеет вид:
Yi = α0 + α1 xi 1 + α2 xi 2 +... + α mxim + ε i (4.1)
Коэффициент регрессии α j показывает, на какую величину в среднем изменится результативный признак Y, если переменную xj увеличить на единицу измерения, т.е. α j является нормативным коэффициентом. Обычно предполагается, что случайная величина ε i имеет нормальный закон распределения с математическим ожиданием равным нулю и с дисперсией σ2.
Анализ уравнения (4.1) и методика определения параметров становятся более наглядными, а расчетные процедуры существенно упрощаются, если воспользоваться матричной формой записи уравнения (4.2):
Y = X α + ε (4.2)
где Y — вектор зависимой переменной размерности n ×1, представляющий собой n наблюдений значений yj,
X — матрица n наблюдений независимых переменных Х 1, Х 2, Х 3,..., Хm, размерность матрицы X равна n ×(m +1);
α — подлежащий оцениванию вектор неизвестных параметров размерности (m +1) ×1;
ε — вектор случайных отклонений (возмущений) размерности n ×1.
Таким образом, 
Уравнение (4.1) содержит значения неизвестных параметров α0, α1, α2,..., α m. Эти величины оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки. Модель линейной регрессии, в которой вместо истинных значений параметров подставлены их оценки (а именно такие регрессии и применяются на практике), имеет вид:
, (4.3)
где α — вектор оценок параметров; е — вектор «оцененных» отклонений регрессии, остатки регрессии ε = Y - X α; 
— оценка значений Y, равная Ха.
Для построения уравнения множественной регрессии чаще используются следующие функции:
линейная – 
степенная – 
экспонента – 
гипербола -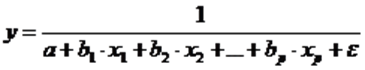 
.
Можно использовать и другие функции, приводимые к линейному виду.
