Эксперимент по методу Монте-Карло позволяет проверить влияние фактора неопр-сти на эндогенную переменную (y – на результат). Эксперимент по методу Монте-Карло подтверждает качество по МНК как наиболее адаптированного метода регрессионного анализа. Если нам удастся получить значения оценок параметров 
близких к самим параметрам, то подтвердится качество метода, на основе к-го происходит оценивание (первая серия экспериментов по методу Монте-Карло).
Если удастся подтвердить, что изменение фатора неопр-сти в k раз приводит к ухудшению (улучшению) оценок, то удастся подвердить влияние фактора на эндогенную переменную – y (вторая серия экспериментов по методу Монте-Карло). В этом заключается вторая серия эксперимента по методу Монте-Карло.
Эксперимент по методу Монте-Карло можно представить в виде четкого алгоритма по каждой серии.
ПЕРВАЯ СЕРИЯ
Первый этап. Исходя из условий имитационного моделирования предполагается, что известны значения параметров.
Второй этап. Формируется массив экзогенных переменных (
, n = 15-20).
Не следует в эксперименте допускать различия на порядок между xi.
Третий этап. На основе предположения о линейности данной зависимости и нормальности распределения CВ Ui формируется массив значений СВ.
Генерация нормально распределенной СВ в табличном процессоре Excel
Осущ-ся через надстройку анализ данных. При настраивании пакета анализа на генерацию случайных чисел учитывают условия Гаусса-Маркова: в поле матожидания ставят 0, в поле дисперсия – 1. Выбирают интервал для получения значений СВ через адресацию.
| 
| ||
| xi | Ui |
| … | |
Ui = 15
Ui = 20
Четвертый этап. Рассчитываются значения эндогенной переменной для каждого наблюдения (
). Мы получили реальные значения эндогенной переменной с учетом осн условий классической моедли (модели Гаусса-Маркова).
Пятый этап. На основе МНК рассчитыаются:
Оценивание параметров в табличном процессоре Excel
1. В свободном месте раб листа книги Excel.
| b | a |
2. Любым известным способом вызывают мастер ф-ий и настраивают его на категрию «статистические». Выбирают ф-ию ЛИНЕЙН () с соотв параметрами. Для настройки параметров с помощью диалогового окна выбирают через адресацию значения 1) эндогенной переменной 2) экзогенной переменной 3) в поле константа поставить цифру 1 4) в поле «статистика» поставить 0.
3. После формирования информации в диалоговом окне (нажать кнопку OK) автоматически в зарезервированных ячейках получим значения коэф-та регрессии и свободной составляющей (константы) a. Для получения константы выполнются след действия: на функциональной клавиатуре нажимается клавиша F2, а затем одновременно комбинация CTRL + Shift + 
Шестой этап. Сравнивают значения параметров и оценок.
Для того, чтобы убедиться в неслучайности данного близкого (или не очень близкого) отклонения требуется повторить первую серию еще 9 раз. В результате получим массив из 10 пар отклонений между реальными значениями параметров и их оценками.
Вывод по первой серии. Требуется сосчитать, сколько “хороших” отклонений удалось получить. В каждом случае исходя из начальных данных ”хороший” вариант опр-ся условно.
В случае, если число “хороших” отклонений больше, чем “плохих”, говорят о том, что МНК дает качественные результаты.
ВТОРАЯ СЕРИЯ
Не изменяются данные первого, второго и третьего этапов. Дополняется третий этап этапом 3*. Арифметически формируется массив Ui* = const5 Ui
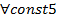
На основе нового массива СВ выполняется пересчет этапов 4, 5 и 6 (везде появляются звездочки). Заметим, что полученные дельты со звездочкой отичаются дельт из первой серии на величину const 5.
Вывод по второй серии. Так как после изменения фактора неопр-сти на const 5 наши отклонения между параметрами и оценками изменились точно на эту const. Это доказывает влияние фактора неопр-сти на регрессионные значения эндогенной переменной.
Оформление очета эксперимент по методу Монте-Карло.
По 1-ой серии: значение 
, всt данные по массивам.
Значения а, b для каждого y.
Отклонения дельта по каждому a и b.
Выделить и сосчитать кол-во “хороших” только бетта-отклонений и отдельно хорошие пары.
Массив x, u1 перенести из первой серии. Параметры альфа и бетта неизменны. Сформировать новый массив, введя константу и указав ее в отчете.
Сделать выводы в конце работы по каждой серии.
