Пусть – линейный оператор. Выберем в
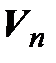какой-либо базис и обозначим А матрицу оператора 
в этом базисе. Если Х – координатный столбец собственного вектора 
в заданном базисе, а 
– соответствующее ему собственное значение, то (4.41) равносильно равенству 
, которое, в свою очередь, равносильно следующему:
. (4.47)
Равенство (4.47) можно рассматривать как матричную запись однородной системы линейных уравнений, причем нас интересуют только ее нетривиальные решения. Как следует из § 5 главы 2, для существования таковых необходимо и достаточно, чтобы выполнялось условие
. (4.48)
Определение. Характеристическим многочленом матрицы А называется многочлен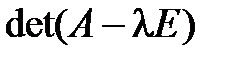 
, уравнение (4.48) называется характеристическим уравнением матрицы А, а корни этого уравнения – ее характеристическими числами.
Лемма 4.2. Подобные матрицы имеют одинаковые характеристические многочлены.
►Пусть матрицы А и 
подобны, значит, существует невырожденная матрица 
такая, что 
. Тогда
Таким образом, матрицы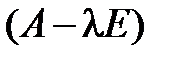 
и (
) тоже подобны, а значит, имеют одинаковые определители.◄
Эта лемма позволяет сформулировать следующее
Определение. Характеристическим многочленом (характеристическим уравнением, характеристическими числами) линейного оператора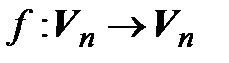 
называется характеристический многочлен (характеристическое уравнение, характеристические числа) его матрицы в некотором, а значит, и в любом базисе.
Из изложенного выше мы видим, что каждое собственное значение линейного оператора 
является корнем его характеристического уравнения, т. е. характеристическим числом. Обратно, если 
– корень уравнения (4.48) и 
, то система (4.47) имеет нетривиальное решение Х 0, значит, АХ 0 =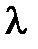 
Х 0 и тогда, если 
– вектор, координатный столбец которого в выбранном базисе совпадает с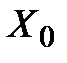 
, то 
, т. е.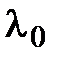 
– собственное значение оператора 
. Если же 
, то оно не может быть собственным значением согласно определению.
Итак, собственные значения линейного оператора – те его характеристические числа, которые принадлежат полю P.
Теперь можно сформулировать следующее правило. Пусть А – матрица линейного оператора в некотором базисе. Чтобы найти собственные векторы оператора поступаем следующим образом:
1) составляем характеристическое уравнение (4.48) матрицы А и находим его корни 
. Те из них, которые принадлежат основному полю, являются собственными значениями (т. е., если Р = С, то все, если Р = R – только действительные);
2) для каждого из полученных собственных значений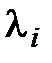 
находим соответствующие ему собственные векторы, решая однородную систему (4.47) при 
.
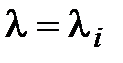Лемма 4.3. Если определитель однородной квадратной системы линейных уравнений
AX = О, (4.49)
равен нулю, то при любом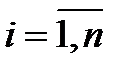 
набор
(
, 
, …, 
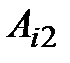), (4.50)
где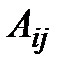 
– алгебраическое дополнение к элементу 
матрицы А, – решение системы (4.49).
►Действительно, подставив (4.50) в каждое из уравнений (4.49), получаем
. (4.51)
Равенство (4.51) верно, так как при 
его левая часть представляет собой разложение 
по 
-й строке, а при 
оно верно на основании теоремы аннулирования. ◄
Пример. Найдем собственные векторы линейного оператора 
, который в некотором базисе пространства V 3 имеет матрицу
.
▼ 1. Составляем характеристический многочлен:
.
Характеристическое уравнение оператора 
выглядит так:
,
а характеристическими числами будут λ1 = 2; λ2 = 3 – i; λ3 = 3 + i. Если P = R, то собственное значение только одно – λ1 = 2; если же P = C, то все значения 
будут собственными. Рассмотрим последний случай.
2. λ1 = 2:
. (4.52)
Однородная система с матрицей (4.52) решается устно: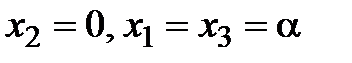 
. Значит, собственные векторы с этим собственным значением выглядят так: 
= α(1; 0; 1), 
.
λ2=3 – i:
. (4.53)
Так как 
, то 
. Поэтому достаточно найти один собственный вектор, а все остальные будут ему коллинеарными. Для нахождения же этого вектора воспользуемся леммой 4.3 и найдем упорядоченный набор из алгебраических дополнений к элементам, например, первой строки матрицы (4.53): 
Тогда все собственные векторы с собственным значением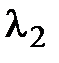 
– это
.
λ3=3 + i:
(4.54)
Заметим, что матрицы (4.53) и (4.54) – комплексно-сопряженные. Значит, и решения систем с этими матрицами – тоже комплексно-сопряженные, и поэтому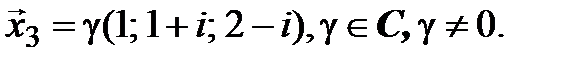 
▲
Вопрос 29
Лемма о диагональном виде матрицы линейного оператора. Определение приводимости квадратной матрицы к диагональному виду и первая теорема о приводимости. Следствие. Замечание о матрице, приводящей матрицу А к диагональному виду
Лемма 4.4. Для того чтобы матрица А линейного оператора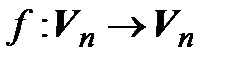 
в некотором базисе пространства 
имела диагональный вид, необходимо и достаточно, чтобы этот базис состоял из собственных векторов оператора f, причем диагональными элементами матрицы А являются собственные значения этого оператора.
►Пусть
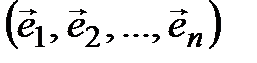– (4.55)
базис пространства , A – матрица оператора f в этом базисе. Тогда
{ А –диагональная} 
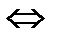{(4.55) состоит из собственных векторов оператора 
а 
– его собственные значения}.◄
Определение. Говорят, что квадратная матрица А с элементами из поля P приводится к диагональному виду над P, если существует невырожденная квадратная матрица Т с элементами из P такая, что матрица 
– диагональная.
Теорема 4.13. Пусть А – квадратная матрица с элементами из поля P, 
– линейное пространство над Р, 
– тот линейный оператор, матрица которого в некотором базисе (4.55) пространства 
совпадает с А. Тогда для приводимости матрицы А к диагональному виду над полем Р необходимо и достаточно, чтобы в существовал базис, состоящий из собственных векторов оператора f.
►Выберем в еще один базис
(4.56)
и обозначим Т матрицу перехода от исходного базиса (4.55) к базису (4.56). Матрица оператора f в этом базисе имеет вид 
. Тогда
{в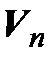 
существует базис (4.56) из собственных векторов оператора f }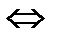
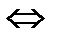{матрица оператора 
в базисе (4.56) диагональная} 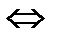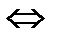{ А приводится к диагональному виду}.◄
Следствие. Если все характеристические числа матрицы А различны и принадлежат полю Р, то А приводится к диагональному виду над Р.
Замечание. Если матрица А приводится к диагональному виду – матрице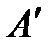 
, то диагональными элементами последней являются собственные значения матрицы А, а матрица Т, приводящая А к диагональному виду, есть не что иное, как матрица перехода от исходного базиса к базису из собственных векторов.
Вопрос 30
