Пусть в линейном пространстве  заданы два базиса:
заданы два базиса:
 (3.41)
(3.41)
и
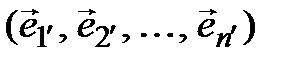 . (3.42)
. (3.42)
Принадлежность вектора второму базису отмечается штрихом, причем удобно штрих ставить не на вектор, а на индекс, например,  – пятый вектор второго базиса. Тогда каждый из векторов второго базиса можно разложить по первому. Все координаты будем обозначать одной и той же ключевой буквой t с двумя индексами: нижним индексом обозначим номер разлагаемого вектора, а верхним – номер координаты. Таким образом,
– пятый вектор второго базиса. Тогда каждый из векторов второго базиса можно разложить по первому. Все координаты будем обозначать одной и той же ключевой буквой t с двумя индексами: нижним индексом обозначим номер разлагаемого вектора, а верхним – номер координаты. Таким образом,
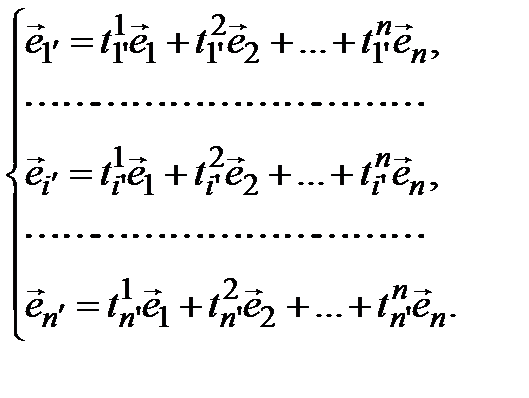 (3.43)
(3.43)
Учитывая нашу договоренность, систему равенств (3.43) можно сокращенно записать одним равенством:
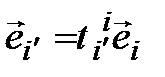 (3.44)
(3.44)
(оцените красоту записи!)
Введем следующие обозначения:

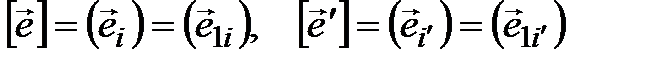
(подчеркиваем, что это матрицы-строки)
 .
.
Тогда  =[располагаем по правилу цепочки] =
=[располагаем по правилу цепочки] =  , откуда вытекает, что
, откуда вытекает, что
 . (3.45)
. (3.45)
Матрицей перехода от базиса (3.41) к базису (3.42) называется матрица Т = 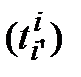 , столбцами которой являются координатные столбцы векторов второго базиса в первом базисе, т. е. матрица, удовлетворяющая системе равенств (3.43) или (3.44), либо одному матричному равенству (3.45).
, столбцами которой являются координатные столбцы векторов второго базиса в первом базисе, т. е. матрица, удовлетворяющая системе равенств (3.43) или (3.44), либо одному матричному равенству (3.45).
Изменение координат вектора при изменении базиса:
Пусть в линейном пространстве  по-прежнему заданы два базиса (3.46) и (3.47). Выберем в
по-прежнему заданы два базиса (3.46) и (3.47). Выберем в  произвольный вектор
произвольный вектор  . Его можно разложить как по одному базису, так и по другому:
. Его можно разложить как по одному базису, так и по другому: 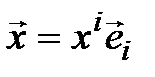 и
и 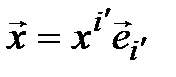 . Тогда
. Тогда
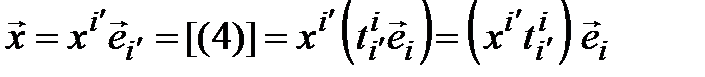 . (3.49)
. (3.49)
Равенство (3.49) – это разложение вектора  по базису (3.46), и поэтому в силу единственности координат вектора в данном базисе получаем
по базису (3.46), и поэтому в силу единственности координат вектора в данном базисе получаем
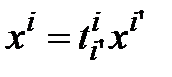 . (3.50)
. (3.50)
Обозначим  координатные столбцы вектора
координатные столбцы вектора  в базисах (3.46) и (3.47) соответственно (
в базисах (3.46) и (3.47) соответственно ( ,
, 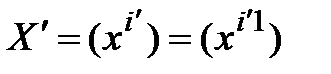 ). Тогда (3.50) равносильно равенству
). Тогда (3.50) равносильно равенству  , из которого вытекает, что
, из которого вытекает, что
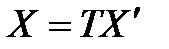 . (3.51)
. (3.51)
Формулы (3.50) и (3.51) показывают, как изменяются координаты вектора при изменении базиса. Равенство (3.51) можно доказать и так:
 .
.
Таким образом,  – координатный столбец вектора
– координатный столбец вектора  в базисе (3.46), поэтому он совпадает с
в базисе (3.46), поэтому он совпадает с  .
.
Вопрос 15
Понятие отображения. Произведение (композиция) отображений. Ассоциативность произведения. Тождественное отображение и его свойства. Взаимно однозначное отображение. Обратное отображение
Понятие отображения
Пусть Х и Y – множества элементов произвольной природы. Говорят, что задано отображение  (читается: отображение f множества X во множество Y), если задан закон, по которому каждому элементу
(читается: отображение f множества X во множество Y), если задан закон, по которому каждому элементу  ставится в соответствие вполне определенный элемент
ставится в соответствие вполне определенный элемент  (рис. 4.1).
(рис. 4.1).
|
|

|

|
Рис. 4.1
Если  , то
, то  называется образом элемента
называется образом элемента  ;
;  – прообразом элемента
– прообразом элемента  при отображении f.
при отображении f.
Примерами отображений являются функции, которые изучаются в школьном курсе математики и в математическом анализе, например, функция  – отображение
– отображение  . Классный журнал является примером отображения множества учеников в классе во множество всех фамилий.
. Классный журнал является примером отображения множества учеников в классе во множество всех фамилий.
Отображение  называется тождественным, если оно любой элемент оставляет на месте. Тождественное отображение множества X на себя будем обозначать
называется тождественным, если оно любой элемент оставляет на месте. Тождественное отображение множества X на себя будем обозначать  . Таким образом,
. Таким образом,  .
.
Отображение  называется взаимно однозначным (или биективным, или биекцией), если оно удовлетворяет двум условиям:
называется взаимно однозначным (или биективным, или биекцией), если оно удовлетворяет двум условиям:
1. 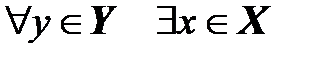 такой, что
такой, что  .
.
2. 
или одному, эквивалентному им, третьему условию:
3.  такой, что
такой, что 
Хороший пример взаимно однозначного отображения: в театре дают билет, каждому билету соответствует некоторое кресло, причем только одно.
Отображения 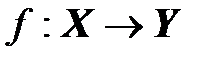 и
и 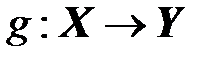 называются равными, если
называются равными, если  .
.
Пусть заданы отображения  и
и  . Произведением (или композицией) отображений f и g называется отображение
. Произведением (или композицией) отображений f и g называется отображение  такое, что
такое, что  (рис. 4.2).
(рис. 4.2).
|
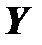
|

|

|

|

|

|

|

|
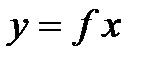
|

|

|
Рис. 4.2
Замечание. В произведении отображений сначала действует внутреннее, а затем внешнее отображение.
Примером произведения отображений является сложная функция.
Лемма 4.1. Произведение отображений ассоциативно, т. е. если заданы отображения  ,
, 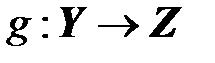 и
и  , то
, то
 .
.
uДля доказательства равенства отображений  и
и 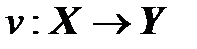 нужно показать, что
нужно показать, что  .
.
Итак, выберем произвольное 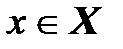 . Тогда
. Тогда
 ; (4.1)
; (4.1)
 (4.2)
(4.2)
Сравнивая (4.1) и (4.2), видим, что  :
:  и поэтому,
и поэтому,  .t
.t
Отображение  называется обратным к отображению
называется обратным к отображению  , если
, если 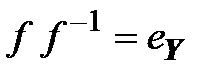 и
и  (рис. 4.3).
(рис. 4.3).
|
|

|

|

|
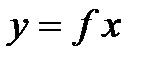
|
Рис. 4.3
Вопрос 16






