Определение. Подмножество W линейного пространства V над P называется его подпространством, если оно само является линейным пространством относительно операций, заданных в V.
Например, R является подпространством пространства С над R (но не С над С), пространство всех непрерывных функций – подпространство пространства функций, заданных на всей числовой прямой. Любое линейное пространство V имеет два тривиальных подпространства: V и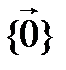 
.
Теорема 3.4. Для того чтобы непустое подмножество W линейного пространства V над P было его подпространством, необходимо и достаточно, чтобы W было замкнуто относительно операций, заданных в V, т. е. чтобы выполнялись условия:
1) 
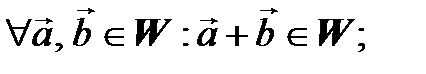
2) 
.
►Необходимость. Пусть W – подпространство пространства V, значит, W – само линейное пространство относительно тех же операций, поэтому внутренняя и внешняя операции в V являются соответственно внутренней и внешней для W, следовательно, условия 1 и 2 выполняются.
Достаточность. Пусть теперь выполняются условия 1 и 2. Тогда операции, заданные в V, для W являются соответственно внутренней и внешней. Остается доказать выполнение аксиом из определения линейного пространства.
Аксиомы 1*, 2* и 5* – 8* в W выполняются, так как они выполняются в V (например, 
).
Если 
– нейтральный элемент в V, то, конечно же, 
Но попал ли 
в W? Так как 
, то 
, и тогда на основании 2-го условия 
Таким образом, если W замкнуто относительно внешней операции, то оно обязательно содержит нейтральный элемент пространства V, а значит, аксиома 3* из определения линейного пространства выполняется.
Пусть 
. Тогда 
и 
. Опять вопрос: попал ли 
в W? И опять, на основании второго условия теоремы, 
, а значит, и аксиома 4* из определения линейного пространства также выполняется. t
Вопрос 9
Линейные оболочки
Определение. Линейной оболочкой системы элементов
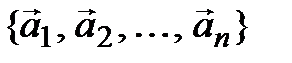(3.36)
линейного пространства V над P называется множество
т. е. это множество всевозможных линейных комбинаций элементов системы (3.36) (система (3.36) может быть и бесконечной).
Примерами могут служить: 
– множество всех векторов, параллельных плоскости Oxy, 
, совпадающая с предыдущей; 
– множество многочленов степени не выше двух.
Теорема 3.5. Линейная оболочка произвольной системы векторов линейного пространства V над P является его подпространством, причем размерность линейной оболочки некоторой системы совпадает с максимальным количеством ее линейно независимых векторов.
► Выберем произвольные векторы 
и произвольное число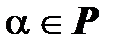 
,
,
Тогда 
, а также 
Таким образом, на основании теоремы 3.4 
является подпространством пространства V.
Пусть m – максимальное количество линейно независимых элементов в (3.36) (
и пусть подсистема
– (3.37)
линейно независима (если это не так, переставим линейно независимые элементы на первые места). Имеем, во-первых,
.
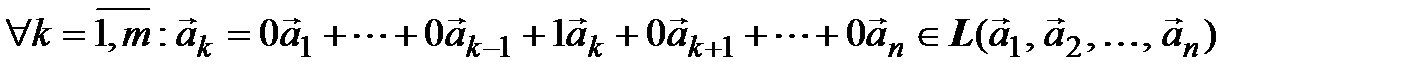Во-вторых, так как m – максимальное количество линейно независимых элементов в (3.36), то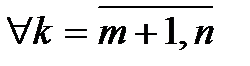 
система 
линейно зависима, а значит, на основании свойства 4º линейной зависимости (§ 2),
такие, что 
. Следовательно,
: 
[замена индекса] = = 
.
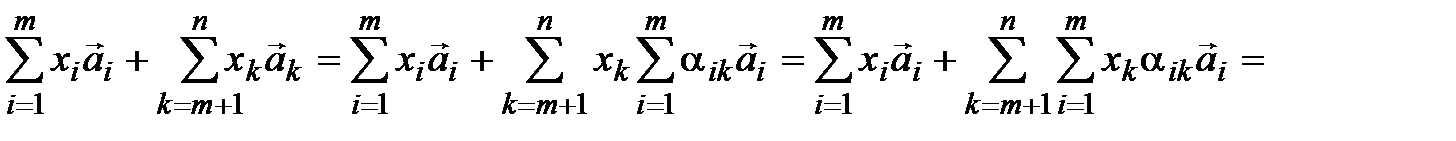
Таким образом, (3.37) – система образующих в 
, а значит, и базис, поэтому 
.t
Вопрос 10
