Определение.Изоморфизмом линейных пространств называется взаимно однозначный линейный оператор. Если существует изоморфизм 
, то линейные пространства 
и 
называются изоморфными. Изоморфизм обозначается так: 
.
Так как изоморфизм – взаимно однозначное отображение, то изоморфные объекты содержат одинаковое количество элементов. Кроме того, в силу линейности, действия, производимые над элементами пространства , одновременно производятся и над элементами пространства . Поэтому в математике изоморфные объекты не различаются.
Теорема 4.8. Изоморфные линейные пространства имеют одинаковые размерности.
►Пусть 
и пусть 
– изоморфизм. Выберем в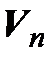 
какой-либо базис
(4.27)
и покажем, что система
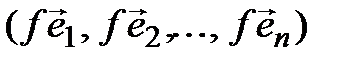– (4.28)
базис пространства 
. Действительно, в силу взаимной однозначности f, 
единственный 
такой, что 
. Тогда, если 
, то 
. Значит, (4.28) – система образующих в 
.
Докажем теперь линейную независимость (4.28).
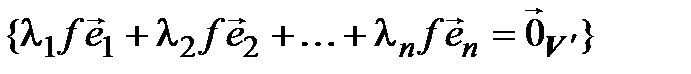
[линейность f ]
[взаимная однозначность f ] 
[линейная независимость (4.27)] 
{(4.28) – линейно независима}.
Таким образом, (4.28) – базис в , а значит, 
. ◄
Вопрос 25
Определение изоморфизма линейных пространств. Теорема об изоморфизме пространств одинаковой размерности
Определение.Изоморфизмом линейных пространств называется взаимно однозначный линейный оператор. Если существует изоморфизм , то линейные пространства и называются изоморфными. Изоморфизм обозначается так: .
Так как изоморфизм – взаимно однозначное отображение, то изоморфные объекты содержат одинаковое количество элементов. Кроме того, в силу линейности, действия, производимые над элементами пространства , одновременно производятся и над элементами пространства . Поэтому в математике изоморфные объекты не различаются.
Теорема 4.9. Все n -мерные линейные пространства над полем Р изоморфны между собой, т. е. существует единственное с точностью до изоморфизма n- мерное линейное пространство над полем Р.
►а) Докажем, что 
.
Выберем в 
какой-либо базис 
. Тогда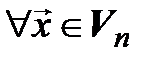 
: . Обозначим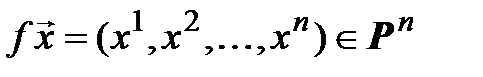 
. Очевидно, отображение 
– взаимно однозначное. Кроме того, 
, 
:
: 
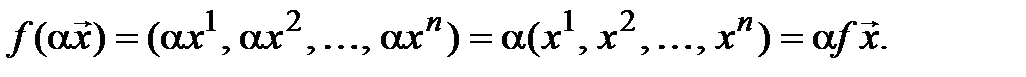
Поэтому f – линейный оператор, а значит, и изоморфизм. Итак, 
.
б) Пусть теперь 
и 
– n- мерные линейные пространства над одним и тем же полем Р. Тогда
{ и 
} 
[симметричность] { и 
и } [транзитивность] { 
}.◄
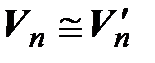Таким образом, мы показали, что с точки зрения математики единственным n- мерным линейным пространством над полем Р является 
.
Вопрос 26
Линейные формы
Определение.Линейной формой на линейном пространстве над полем 
называется линейный оператор 
.
Мы уже знаем, что множество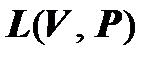 
всех линейных форм на линейном пространстве также является линейным пространством над тем же полем, что и , относительно операций сложения линейных форм и умножения линейной формы на число. Пространство 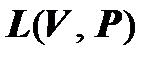будем называть сопряженным пространству , и обозначать 
, его элементы назовем ковекторами и тоже для удобства отметим стрелками, но снизу (например, 
).
Рассмотрим 
-мерное линейное пространство 
и выберем в нем какой-либо базис:
. (4.37)
Пусть 
– произвольный вектор пространства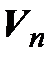 
, 
– линейная форма. Тогда
. (4.38)
Мы видим, что значение линейной формы для вектора 
зависит от его координат и некоторых чисел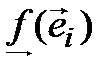 
, вовсе с вектором 
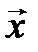не связанных. Обозначим 
и назовем эти числа компонентами формы 
в базисе (4.37). Теперь (4.38) можно переписать и так: 
.
Выберем в 
ещё один базис
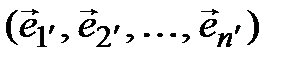(4.39)
и обозначим 
компоненты линейной формы в базисе (4.39).Тогда
= 
= [определение матрицы перехода] = 
=
= [линейность ] = 
.
Мы получили закон изменения компонент линейной формы при изменении базиса.
В пространстве линейных форм 
выберем линейных форм
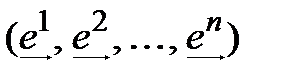(4.40)
по следующему принципу:
,
т. е. форма 
принимает значение, равное 0, для всех базисных векторов, за исключением одного,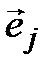 
, для которого она принимает значение, равное 1. Существование таких форм вытекает из теоремы 4.1. Докажем линейную независимость (4.40). Как обычно, составим линейную комбинацию и приравняем ее нейтральному элементу.
{(4.40) линейно независима}.
Пусть теперь 
– произвольная линейная форма, 
– ее компоненты в базисе (4.40). Обозначим 
. Тогда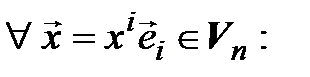 
Таким образом, = , следовательно, система (4.40) в пространстве 
является системой образующих, а значит, и базисом. Итак, пространство, сопряженное к конечномерному линейному пространству, имеет ту же размерность. Базисы (4.37) и (4.40) пространств 
и 
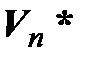называются сопряженными или взаимными. Следовательно, компоненты линейной формы 
в базисе (4.37) пространства 
– это её координаты во взаимном базисе пространства 
.
Вопрос 27
