Об’єм вибірки може бути не настільки великим (наприклад, десятки спостережень), щоб використовувати формулу 
замість
точної 
. В той же час, розподіл вибіркової частки w можна, як і раніше, вважати наближено-нормальним. В цьому випадку довірчий інтервал для генеральної частки слід шукати з умови
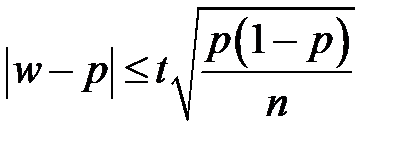. Піднесемо обидві частини цієї нерівності в квадрат, зведемо її до рівносильної: 
.
Областю розв’язку цієї нерівності є внутрішня частина еліпса, що проходить через точки (0;0) і (1;1) і має в цих точках дотичні, паралельні осі абсцис. Оскільки величина w знаходиться між 0 і 1, то область D необхідно ще обмежити зліва і справа прямими 
і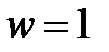 
(наявність «зайвих областей», що виходять за смугу 
, пояснюється тим, що при значеннях p, близьких до 0 чи 1 припущення про нормальний закон розподілу w стає неправомірним). За знайденим по вибірці значенням w межі довірчого інтервалу 
для p визначаються як точки перетину відповідної вертикальної прямої з еліпсом (рис. 3.2).
Чим більший об’єм вибірки n, тим «довірчий еліпс» більш витягнутий, тим вужчий довірчий інтервал. Границ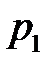і 
і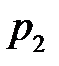 
довірчого інтервалу для p можуть бути знайдені за формулою:
.
У випадку великих вибірок, при 
, величинами 
(у порівнянні з 1), 
(у порівнянні з w), 
(у порівнянні з 
) можна знехтувати, і отримаємо:
.
Рис. 3.2
◄ Приклад 3.5 З партії, що містить близько 2000 деталей, для перевірки за схемою власно-випадкової безповторної вибірки було відібрано 200 деталей, серед яких виявилось 184 стандартних. Знайти: а) ймовірність того, що частка нестандартних деталей у всій партії відрізняється від отриманої частки у вибірці не більше, ніж на 0,02 (за абсолютною величиною); б) межі, в яких з надійністю 0,95 знаходиться частка нестандартних деталей в партії; в) знайти границі, в яких з надійністю 0,95 знаходиться частка p нестандартних виробів у всій партії, вважаючи n =50, w =0.08, 
.
Розв’язання. Маємо 
, 
, 
нестандартних деталей 
.
а) Знайдемо середню квадратичну похибку безповторної вибірки для частки: 
.
Тепер знайдемо шукану довірчу ймовірність:
, тобто ймовірність того, що вибрана частка нестандартних деталей буде відрізнятись від генеральної частки не більше ніж на 0,02 (по абсолютній величині), дорівнює 0,729.
б) Враховуючи, що 
і (за таблицею для значень функції Лапласа) 
, знайдемо граничну похибку вибірки для частки: 
. Тепер визначаємо шуканий довірчий інтервал: 
або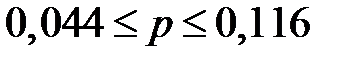 
. Отже, з надійністю 0,95 частка нестандартних деталей у всій партії знаходиться в межах від 0,044 до 0,116.
в) Вважаючи, що t = 1,96, знайдемо довірчі границі для генеральної частки p:
= 
або p 1=0,032, p 2=0,188, тобто з надійністю 0,95 частка нестандартних виробів у всій партії знаходиться в проміжку від 0,032 до 0,188.►
