Власновипадковою вибіркою. Оцінка генеральної частки
Нехай генеральна сукупність містить N елементів, з яких M мають деяку ознаку A. Необхідно знайти «найкращу» оцінку генеральної частки 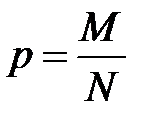 . Розглянемо в якості такої можливої оцінки параметра p його статистичний аналог – вибіркову частку
. Розглянемо в якості такої можливої оцінки параметра p його статистичний аналог – вибіркову частку 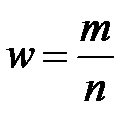 .
.
А) Вибірка повторна
Вибіркову частку можна подати як середнє арифметичне n альтернативних випадкових величин 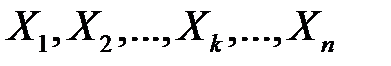 , тобто
, тобто 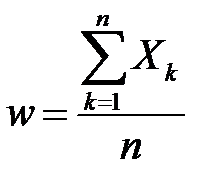 , де кожна випадкова величина
, де кожна випадкова величина 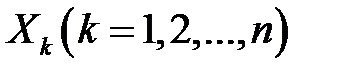 виражає кількість появ ознаки в k- му елементі вибірки (тобто при наявності ознаки
виражає кількість появ ознаки в k- му елементі вибірки (тобто при наявності ознаки 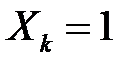 , при її відсутності
, при її відсутності 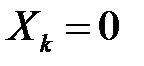 ) і має один і той самий закон розподілу:
) і має один і той самий закон розподілу:
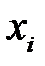
| ||
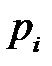
| 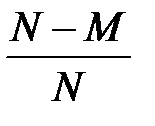
| 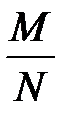
|
Дійсно, ймовірність того, що 1-й відібраний у вибірку елемент має ознаку A згідно із класичним означенням ймовірності рівна 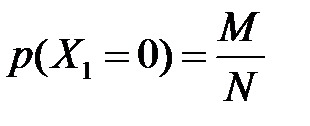 . Так як вибірка повторна, то кожен елемент знову повертається у вихідну сукупність, відновлюючи кожного разу її початковий склад і об’єм, то ймовірності
. Так як вибірка повторна, то кожен елемент знову повертається у вихідну сукупність, відновлюючи кожного разу її початковий склад і об’єм, то ймовірності 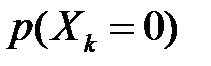 та
та 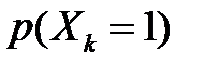 залишаються тими ж самими для будь-якого елемента вибірки, і закон розподілу
залишаються тими ж самими для будь-якого елемента вибірки, і закон розподілу 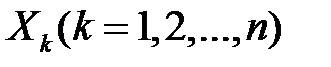 один і той самий.
один і той самий.
Випадкові величини 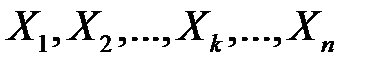 незалежні, оскільки незалеж
незалежні, оскільки незалеж
ними є будь-які події 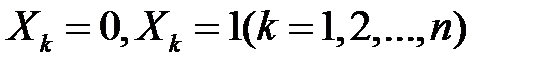 та їх комбінації. Наприклад, незалежні події
та їх комбінації. Наприклад, незалежні події 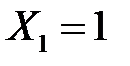 та
та 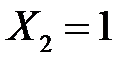 , так як
, так як 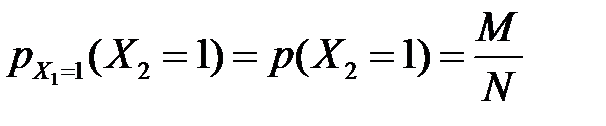 , тобто ймовірність того, що 2-й відібраний у вибірку елемент має ознаку A, не змінюється в залежності від того, чи мав ознаку A 1-й елемент чи ні і т.д.
, тобто ймовірність того, що 2-й відібраний у вибірку елемент має ознаку A, не змінюється в залежності від того, чи мав ознаку A 1-й елемент чи ні і т.д.
Теорема 2.1 Вибіркова частка 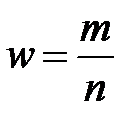 повторної вибірки є незміщеною і спроможною оцінкою генеральної частки
повторної вибірки є незміщеною і спроможною оцінкою генеральної частки 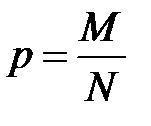 , причому її
, причому її
дисперсія 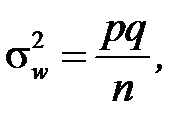 де
де 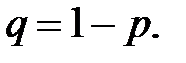 (2.7)
(2.7)
Доведення. Доведемо спочатку незміщеність оцінки 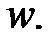 Математичне сподівання і дисперсія частості події в n незалежних випробуваннях, в кожному з яких вона може настати з однією і тією ж ймовірністю p рівні відповідно
Математичне сподівання і дисперсія частості події в n незалежних випробуваннях, в кожному з яких вона може настати з однією і тією ж ймовірністю p рівні відповідно 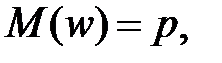
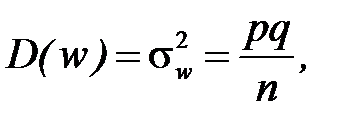 або
або 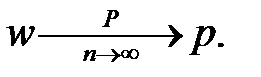 Оскільки ймовірність того, що будь-який вибраний елемент має ознаку А, є генеральна доля р, то з першої рівності випливає, що частість або вибіркова доля w є незміщена оцінка генеральної долі р.
Оскільки ймовірність того, що будь-який вибраний елемент має ознаку А, є генеральна доля р, то з першої рівності випливає, що частість або вибіркова доля w є незміщена оцінка генеральної долі р.
Доведемо спроможність оцінки 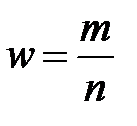 , яка випливає безпосередньо з теореми Бернуллі
, яка випливає безпосередньо з теореми Бернуллі 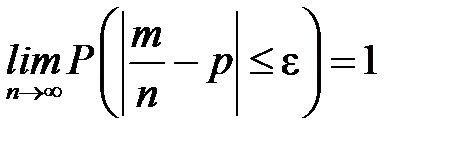 .
.
Б) Вибірка безповторна
У випадку безповторної вибірки випадкові величини 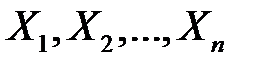 будуть залежними. Розглянемо, наприклад, події
будуть залежними. Розглянемо, наприклад, події 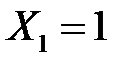 і
і 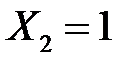 . Тепер ймовірність
. Тепер ймовірність 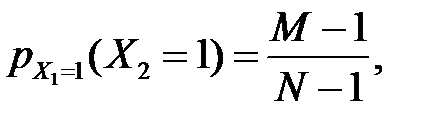 оскільки відібраний елемент у вихідну сукупність не повертається, то в ній залишається всього N – 1 елементів, з яких ознаку A мають M – 1.Ця ймовірність
оскільки відібраний елемент у вихідну сукупність не повертається, то в ній залишається всього N – 1 елементів, з яких ознаку A мають M – 1.Ця ймовірність 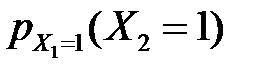 не дорівнює
не дорівнює 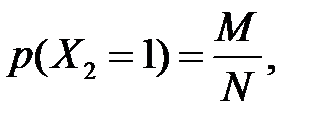 тобто події
тобто події 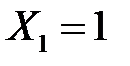 і
і 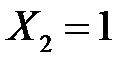 - залежні. Аналогічно будуть залежними будь-які події
- залежні. Аналогічно будуть залежними будь-які події 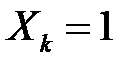 ,
, 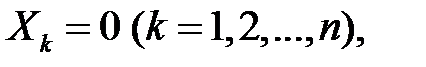 а це означає, що залежними є випадкові величини
а це означає, що залежними є випадкові величини 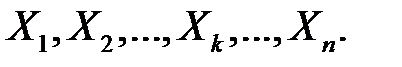
Теорема 2.2 Вибіркова частка 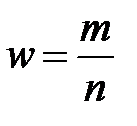 безповторної вибірки є незміщеною і спроможною оцінкою генеральної частки
безповторної вибірки є незміщеною і спроможною оцінкою генеральної частки 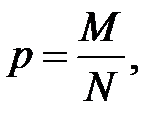 причому її дисперсія
причому її дисперсія 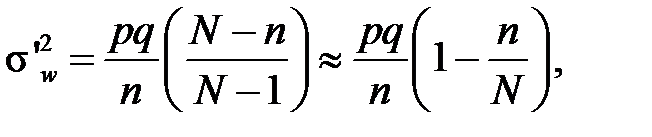 де
де 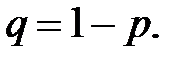 (2.8)
(2.8)
Доведення. Очевидно, що і для безповторної вибірки 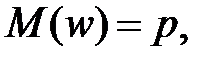 тобто w – незміщена оцінка для генеральної частки
тобто w – незміщена оцінка для генеральної частки 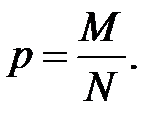 Це пов’язано з тим, що математичне сподівання суми будь-яких двох випадкових величин дорівнює сумі їх математичних сподівань (в тому числі суми залежних випадкових величин, якою є вибіркова частка w безповторної вибірки).
Це пов’язано з тим, що математичне сподівання суми будь-яких двох випадкових величин дорівнює сумі їх математичних сподівань (в тому числі суми залежних випадкових величин, якою є вибіркова частка w безповторної вибірки).
Знайдемо дисперсію вибіркової частки для безповторної вибірки:
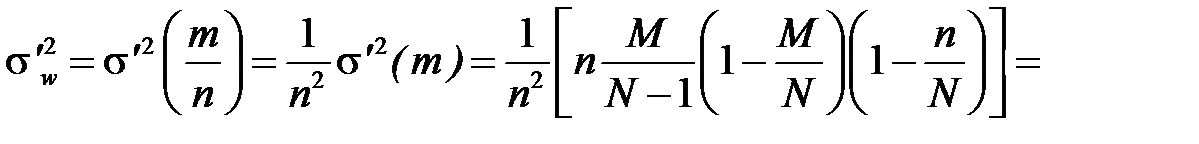
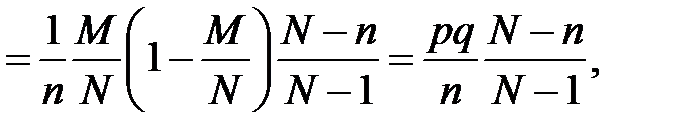 де
де 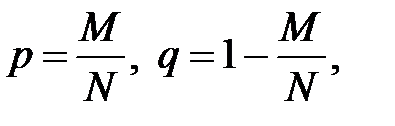
тобто вірною є формула ( 2.8 )(при виведенні формули для 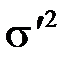 використовували те, що випадкова величина
використовували те, що випадкова величина 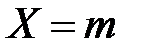 у випадку безповторної вибірки має гіпергеометричний розподіл, і її дисперсія визначається за формулою
у випадку безповторної вибірки має гіпергеометричний розподіл, і її дисперсія визначається за формулою 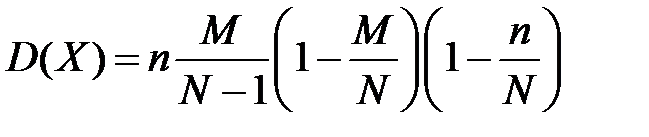 .
.
Для того, щоб легше було зрозуміти формулу (2.8), розглянемо її частинні випадки і переконаємося в справедливості цієї формули:
1. При 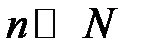
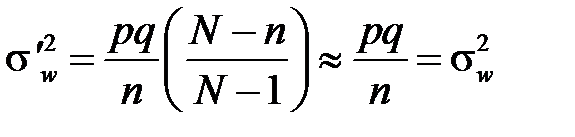 , тобто якщо об’єм вибірки
, тобто якщо об’єм вибірки
значно менший від об’єму генеральної сукупності, то вибірка практично не відрізняється від повторної, і дисперсії вибіркової частки 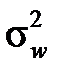 і
і 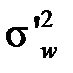 наближено рівні.
наближено рівні.
2. При 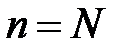
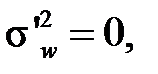 тобто, якщо припустити, що об’єм вибірки рівний
тобто, якщо припустити, що об’єм вибірки рівний
об’єму генеральної сукупності, то вибіркова частка буде рівна генеральній частці, і її дисперсія буде дорівнювати нулю.
◄ Приклад 2.5 Знайти незміщену і спроможну оцінку частки робітників цеху із виробітком не меншим 124% за вибіркою, поданою у табл.1.1 (розділ 1).
Розв’язання. Незміщеною і спроможною оцінкою генеральної частки 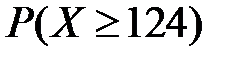 є вибіркова частка
є вибіркова частка
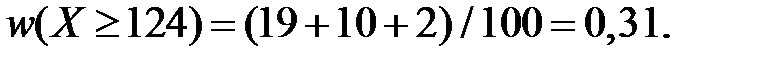 ►
►




