1. Дозволяє суттєво економити на витраті ресурсів (матеріальних, трудових, часових);
2. Являється єдино можливиму випадку нескінченної генеральної сукупності чи у випадку, коли дослідження пов’язане зі знищенням об’єктів, за якими ведеться спостереження (наприклад, дослідження довговічності електричних лампочок, граничних режимів роботи приладів і т.п.);
3. При тих самих витратах ресурсів дає можливість проведення поглибленого дослідження за рахунок розширення програми дослідження;
4. Дозволяє знизити похибки реєстрації, тобто розбіжності між істинним та зареєстрованим значеннями ознаки.
Основний недолік вибіркового методу – похибки дослідження, чи похибки репрезентативності (представництва).
Для того, щоб за даними вибірки мати можливість робити висновки про генеральну сукупність, вона повинна бути вибрана випадково. Випадковість відбору елементів у вибірку досягається дотриманням принципу рівної можливості всім елементам генеральної сукупності бути відібраними. На практиці це досягається тим, що постачання елементів у вибірку проводиться методом жеребкування (лотереї) чи за допомогою випадкових чисел, що містяться у спеціальних таблицях, чи вироблених ЕОМ за допомогою датчика випадкових чисел.
Вибірка називається репрезентативною (представницькою), якщо вона достатньо добре відтворює генеральну сукупність.
Розрізняють наступні види вибірок:
1. власно-випадкова вибірка, утворена випадковим вибором елементів
без роздроблення на частини чи групи;
2. механічна вибірка, в яку елементи з генеральної сукупності вибира-
ються через певний інтервал. Наприклад, якщо об’єм вибірки має складати 10% (10%-на вибірка), то відбирається кожний 10-й її елемент і т.д.;
3. типова (стратифікована) вибірка, в яку випадковим чином відбира-
ються елементи з типових груп, на які за деякою ознакою розбивається генеральна сукупність;
4. серійна (гніздова) вибірка, в яку випадковим чином відбираються не
елементи, а цілі групи сукупності (серії), а самі серії підлягають загальному спостереженню.
Використовують два способи утворення вибірки:
- повторний відбір (за схемою поверненої кулі), коли кожен елемент, випадково відібраний і досліджений, повертається у загальну сукупність і може бути повторно відібраним;
- безповторний відбір (за схемою неповерненої кулі), коли відібраний елемент не повертається у загальну сукупність.
Математична теорія вибіркового методу базується на аналізі власно-випадкової вибірки. Розглядом цієї вибірки ми і обмежимось.
Позначимо
 – значення ознаки (випадкової величини
– значення ознаки (випадкової величини 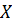 );
);
N та n – об’єми генеральної та вибіркової сукупностей;
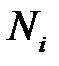 та
та 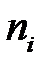 – кількість елементів генеральної та вибіркової сукупностей зі значеннями ознаки
– кількість елементів генеральної та вибіркової сукупностей зі значеннями ознаки 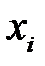 ;
;
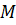 та
та 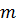 – кількість елементів генеральної та вибіркової сукупностей, що мають дану ознаку.
– кількість елементів генеральної та вибіркової сукупностей, що мають дану ознаку.
Середні арифметичні розподілу ознаки в генеральній та вибірковій сукупностях називаються відповідно генеральним та вибірковим середнім,
а дисперсії цих розподілів – генеральною та вибірковою дисперсіями.
Відношення кількості елементів генеральної та вибіркової сукупностей, що мають певні ознаки 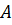 , до їх об’ємів, називаються відповідно генеральною і вибірковою частками. Всі формули зведемо в таблицю 2.1.
, до їх об’ємів, називаються відповідно генеральною і вибірковою частками. Всі формули зведемо в таблицю 2.1.
Таблиця 2.1
| Найменування характеристики | Генеральна сукупність | Вибірка |
| Середнє | 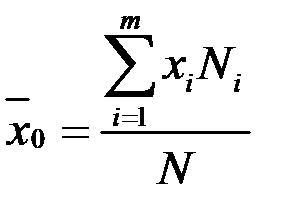 (2.1) (2.1)
|  (2.2) (2.2)
|
| Дисперсія |  (2.3) (2.3)
| 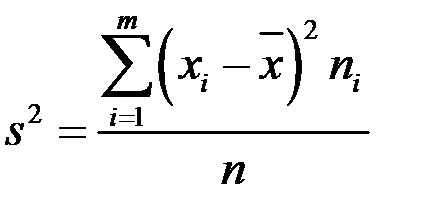 (2.4) (2.4)
|
| Частка | 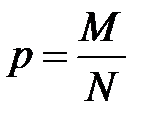 (2.5) (2.5)
| 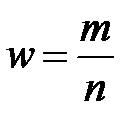 (2.6) (2.6)
|
Найважливішим завданням вибіркового методу є оцінка параметрів (характеристик) генеральної сукупності за даними вибірки. Теоретичною основою застосування вибіркового методу є закон великих чисел, згідно з яким при необмеженому збільшенні об’єму вибірки практично вірогідно, що випадкові вибіркові характеристики як завгодно близько наближаються (збігаються за ймовірністю) до певних параметрів генеральної сукупності.
Поняття оцінки параметрів
Нехай розподіл ознаки X – генеральної сукупності – задається функцією ймовірностей 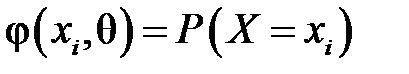 (для дискретної випадкової величини X) або густиною ймовірностей
(для дискретної випадкової величини X) або густиною ймовірностей 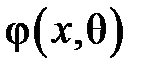 (для неперервної випадкової величини X), яка містить невідомий параметр θ. Наприклад, це параметр λ в розподілі Пуассона чи параметри a та
(для неперервної випадкової величини X), яка містить невідомий параметр θ. Наприклад, це параметр λ в розподілі Пуассона чи параметри a та 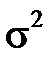 для нормального закону розподілу і т.д. Про параметр θ намагаються судити по вибірці, що складається із значень (варіант)
для нормального закону розподілу і т.д. Про параметр θ намагаються судити по вибірці, що складається із значень (варіант)  . Ці значення можна розглядати як частинні значення (реалізації) n незалежних випадкових величин
. Ці значення можна розглядати як частинні значення (реалізації) n незалежних випадкових величин 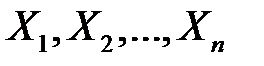 ,кожна з яких має той самий закон розподілу, що й сама випадкова величина X.
,кожна з яких має той самий закон розподілу, що й сама випадкова величина X.
Означення 2.1Оцінкою 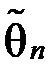 параметра θ називають кожну функцію результатів спостереження над випадковою величиною X (по-іншому – статистику), за допомогою якої роблять висновки про значення параметра θ:
параметра θ називають кожну функцію результатів спостереження над випадковою величиною X (по-іншому – статистику), за допомогою якої роблять висновки про значення параметра θ: 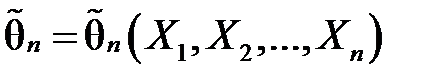 .
.
Оскільки 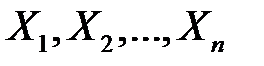 – випадкові величини, то і оцінка
– випадкові величини, то і оцінка  (на відміну від параметра, що оцінюється – величини невипадкової) є випадковою величиною, яка залежить від закону розподілу випадкової величини X та числа n.
(на відміну від параметра, що оцінюється – величини невипадкової) є випадковою величиною, яка залежить від закону розподілу випадкової величини X та числа n.
Завжди існує множина функцій від результатів спостережень  (від n «екземплярів» випадкової величини X), які можна запропонувати в якості параметра θ. Наприклад, якщо параметр θ є математичним сподіванням величини X, тобто генерального середнього
(від n «екземплярів» випадкової величини X), які можна запропонувати в якості параметра θ. Наприклад, якщо параметр θ є математичним сподіванням величини X, тобто генерального середнього 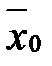 , то в якості його оцінки
, то в якості його оцінки 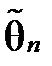 по вибірці можна взяти: середнє арифметичне результатів спостережень – вибіркове середнє
по вибірці можна взяти: середнє арифметичне результатів спостережень – вибіркове середнє 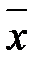 , моду
, моду 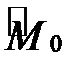 , медіану
, медіану 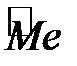 , півсуму найбільшого і найменшого значень у вибірці, тобто
, півсуму найбільшого і найменшого значень у вибірці, тобто 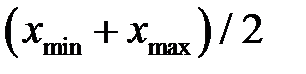 і т.д. Про якість оцінки слід судити не за її індивідуальними значеннями, а лише за розподілом її значень у великій мережі дослідів, тобто за вибірковим розподілом оцінки. Для того, щоб значення
і т.д. Про якість оцінки слід судити не за її індивідуальними значеннями, а лише за розподілом її значень у великій мережі дослідів, тобто за вибірковим розподілом оцінки. Для того, щоб значення 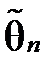 було близьким до θ, необхідно поставити вимогу, щоб розкид випадкової величини
було близьким до θ, необхідно поставити вимогу, щоб розкид випадкової величини 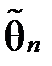 відносно θ (що виражається, наприклад, математичним сподіванням квадрата відхилення оцінки від параметра, що оцінюється
відносно θ (що виражається, наприклад, математичним сподіванням квадрата відхилення оцінки від параметра, що оцінюється 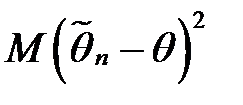 ) був найменшим. Така основна умова, яку має задовольняти «найкраща» оцінка.
) був найменшим. Така основна умова, яку має задовольняти «найкраща» оцінка.
Властивості оцінок
Означення 2.2 Оцінка 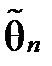 параметра θ називається незміщеною, якщо її математичне сподівання рівне параметру, що оцінюється, тобто
параметра θ називається незміщеною, якщо її математичне сподівання рівне параметру, що оцінюється, тобто 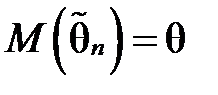 .В іншому випадку оцінка називається зміщеною.
.В іншому випадку оцінка називається зміщеною.
Вимога незміщеності гарантує відсутність систематичних похибок при оцінюванні. Якщо при скінченному об’ємі вибірки n 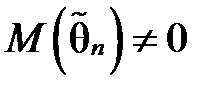 , тобто зміщення оцінки
, тобто зміщення оцінки 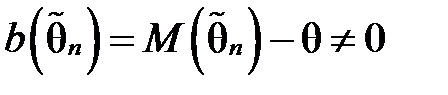 , але
, але 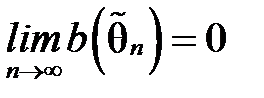 , то така оцінка
, то така оцінка 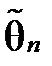 називається асимптотично незміщеною.
називається асимптотично незміщеною.
Означення 2.3 Оцінка 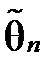 параметра θ називається спроможною, якщо вона задовольняє закону великих чисел, тобто збігається за ймовірністю до параметра, що оцінюється:
параметра θ називається спроможною, якщо вона задовольняє закону великих чисел, тобто збігається за ймовірністю до параметра, що оцінюється: 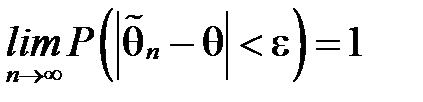 ,
,
У випадку використання спроможних оцінок виправдовується збільшення об’єму вибірки, оскільки при цьому стають малоймовірними значні похибки при оцінюванні. Тому практичне значення мають тільки спроможні оцінки. Якщо оцінка  параметра θ є незміщеною, а її дисперсія
параметра θ є незміщеною, а її дисперсія 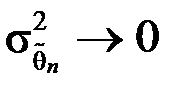 при
при 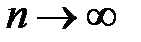 , то оцінка
, то оцінка  є також спроможною.Це безпосередньо випливає з нерівності Чебишова
є також спроможною.Це безпосередньо випливає з нерівності Чебишова 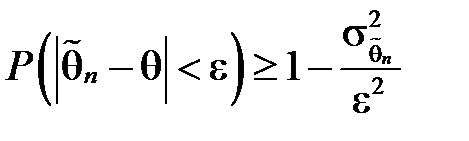 .
.
Означення 2.4 Незміщена оцінка 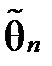 параметра θ називається ефективною, якщо вона має найменшу дисперсію серед усіх можливих незміщених оцінок параметра θ, обчислених за вибірками одного і того самого об’єму n.
параметра θ називається ефективною, якщо вона має найменшу дисперсію серед усіх можливих незміщених оцінок параметра θ, обчислених за вибірками одного і того самого об’єму n.
Оскільки для зміщеної оцінки  існує дисперсія
існує дисперсія 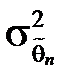 , то ефективність є вирішальною властивістю, яка визначає якість оцінки.
, то ефективність є вирішальною властивістю, яка визначає якість оцінки.
Ефективність оцінки 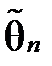 визначають співвідношенням:
визначають співвідношенням: 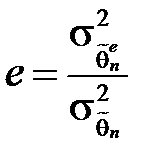 ,
,
де 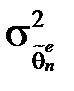 та
та 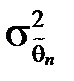 – відповідно дисперсії ефективної та даної оцінок. Чим ближчим є e до 1, тим ефективнішою є оцінка. Якщо
– відповідно дисперсії ефективної та даної оцінок. Чим ближчим є e до 1, тим ефективнішою є оцінка. Якщо 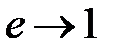 при
при 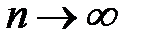 , то така оцінка називається асимптотично ефективною.
, то така оцінка називається асимптотично ефективною.
В якості статистичних оцінок параметрів генеральної сукупності бажано використовувати оцінки, що задовольняють одночасно вимогам незміщеності, спроможності та ефективності. Однак, досягнути цього вдається не завжди.
Методи знаходження оцінок
Метод моментів, запропонований К. Пірсоном.
У цьому методі визначена кількість вибіркових моментів (початкових 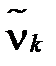 чи центральних
чи центральних 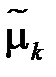 , або тих та інших) прирівнюється до відповідних
, або тих та інших) прирівнюється до відповідних
теоретичних моментів розподілу (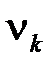 чи
чи 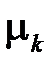 ) випадкової величини X.
) випадкової величини X.
 ,
, 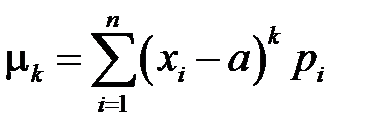 - дискретна випадкова величина з функцією ймовірностей
- дискретна випадкова величина з функцією ймовірностей 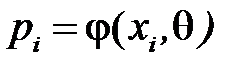 ;
;
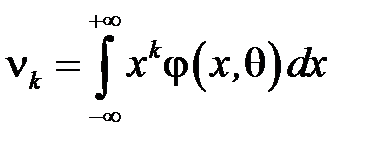 ,
, 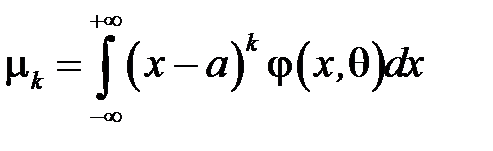 - для неперервної випадкової величини з густиною ймовірностей
- для неперервної випадкової величини з густиною ймовірностей  , де
, де 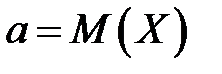 .
.
◄ Приклад 2.1 Знайти оцінку методом моментів для параметра λ закону Пуассона.
Розв’язання. В даному випадку для знаходження єдиного параметра λ достатньо прирівняти теоретичний  та емпіричний
та емпіричний 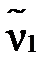 початкові моменти першого порядку.
початкові моменти першого порядку. 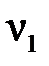 – математичне сподівання випадкової величини X. Для випадкової величини, розподіленої за законом Пуассона,
– математичне сподівання випадкової величини X. Для випадкової величини, розподіленої за законом Пуассона, 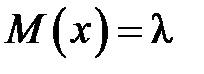 . Момент
. Момент 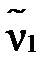 ,згідно з формулою для початкових моментів, дорівнює
,згідно з формулою для початкових моментів, дорівнює  . Звідси, оцінка методом моментів параметра λ закону Пуассона є вибіркове середнє
. Звідси, оцінка методом моментів параметра λ закону Пуассона є вибіркове середнє  .►
.►
Оцінки методом моментів параметра зазвичай спроможні, однак за ефективністю вони не є «найкращими».
Метод максимальної правдоподібності, запропонований Р. Фішером.
Основу методу складає функція правдоподібності, що виражає густину ймовірностей (ймовірність) сумісної появи результатів вибірки 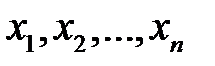 :
:
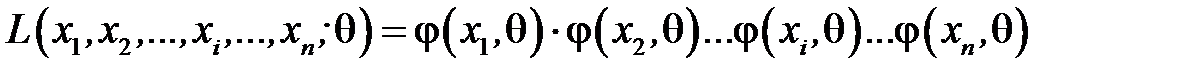 , або
, або
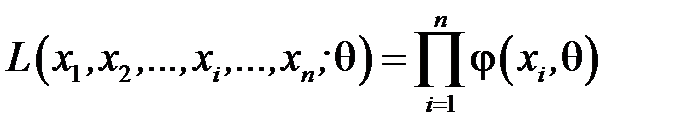 .
.
Згідно з методом максимальної правдоподібності в якості оцінки невідомого параметра θ приймається таке значення 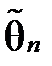 , яке максимізує функцію L.
, яке максимізує функцію L.
Пошук оцінки 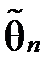 спрощується, якщо максимізувати не саму функцію L, а
спрощується, якщо максимізувати не саму функцію L, а 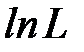 , оскільки максимум обох функцій досягається при одному і тому
, оскільки максимум обох функцій досягається при одному і тому
самому значенні θ. Тому 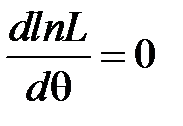 ,
,  . Потім знаходимо точку максимума функції.
. Потім знаходимо точку максимума функції.
◄ Приклад 2.2 Знайти оцінку методом максимальної правдоподібності для ймовірності p настання деякої події A за даним числом m появи цієї події в n незалежних випробуваннях.
Розв’язання. Складемо функцію правдоподібності:
 , або
, або  .
.
Тоді 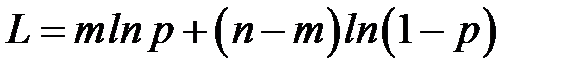 і
і 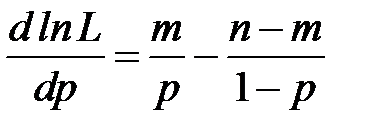 , звідки
, звідки  . Можна показати, що при
. Можна показати, що при  виконується достатня умова екстремуму функції L.
виконується достатня умова екстремуму функції L.
Таким чином, оцінкою методом максимальної правдоподібності ймовірності p події A буде частота 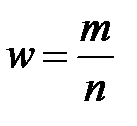 цієї події.►
цієї події.►
◄ Приклад 2.3 Знайти оцінки методом максимальної правдоподібності для параметрів a і 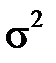 нормального розподілу за даними вибірки.
нормального розподілу за даними вибірки.
Розв’язання. Густина ймовірності нормально розподіленої випадкової величини  . Тоді функція правдоподібності має вигляд:
. Тоді функція правдоподібності має вигляд:
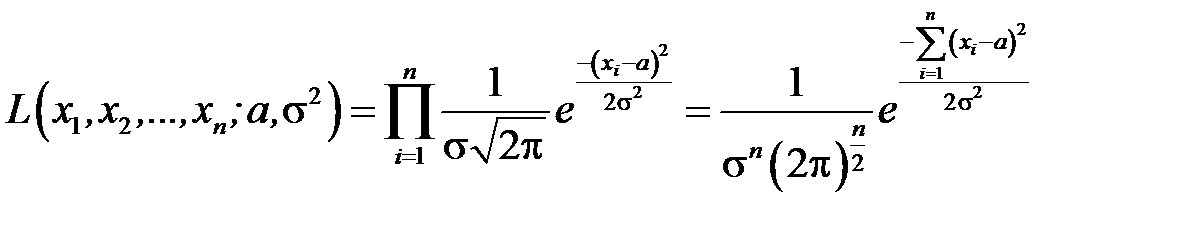 .
.
Прологарифмуємо та отримаємо:
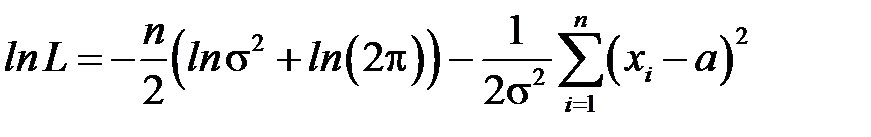 .
.
Для знаходження параметрів a і 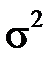 необхідно прирівняти до нуля частинні похідні по параметрах a і
необхідно прирівняти до нуля частинні похідні по параметрах a і 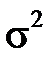 , тобто розв’язати систему рівнянь правдоподібності:
, тобто розв’язати систему рівнянь правдоподібності: 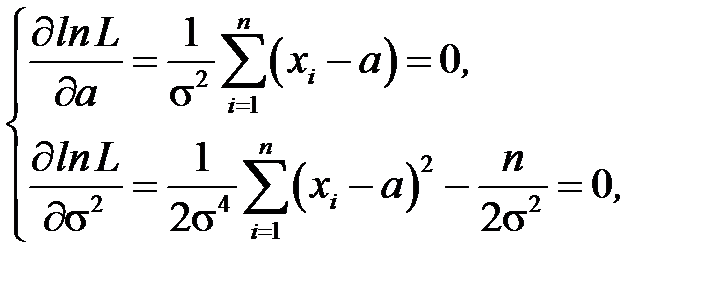
звідки оцінки максимальної правдоподібності рівні:
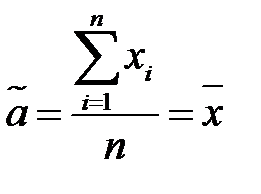 ,
, 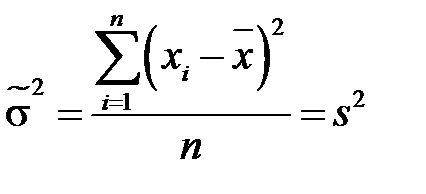 .
.
Таким чином, оцінками методу максимальної правдоподібності математичного сподівання a і дисперсії 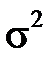 нормально розподіленої випадкової величини є відповідно вибіркове середнє
нормально розподіленої випадкової величини є відповідно вибіркове середнє 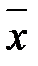 і вибіркова дисперсія
і вибіркова дисперсія 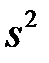 .►
.►
Важливість методу максимальної правдоподібності пов’язана із його оптимальними властивостями. Так, якщо для параметра θ існує ефективна оцінка  , то оцінка максимальної правдоподібності єдина і рівна
, то оцінка максимальної правдоподібності єдина і рівна 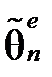 . Крім цього, при достатньо загальних умовах оцінки максимальної правдоподібності є спроможними, асимптотично незміщеними, асимптотично ефективними і мають нормальний розподіл.
. Крім цього, при достатньо загальних умовах оцінки максимальної правдоподібності є спроможними, асимптотично незміщеними, асимптотично ефективними і мають нормальний розподіл.
Основний недолік методу максимальної правдоподібності – важкість обчислення оцінок.
Метод найменших квадратів – один із найбільш простих прийомів побудови оцінок. Він полягає у тому, що оцінка визначається з умови мінімізації суми квадратів відхилень вибіркових даних від шуканої оцінки.
◄Приклад 2.4 Знайти оцінку методом найменших квадратів 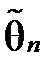 для генерального середнього
для генерального середнього 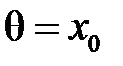 .
.
Розв’язання. Згідно із методом найменших квадратів знайдемо оцінку 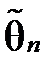 з умови мінімізації суми:
з умови мінімізації суми: 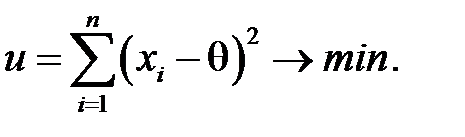 Використовуючи необхідну умову екстремуму, прирівняємо до нуля похідну
Використовуючи необхідну умову екстремуму, прирівняємо до нуля похідну
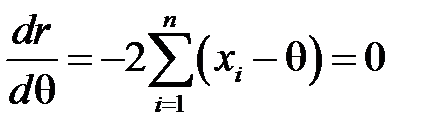 , звідки
, звідки 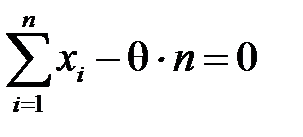 і
і 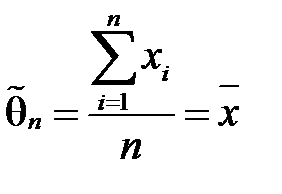 , тобто оцінка методом найменших квадратів генерального середнього
, тобто оцінка методом найменших квадратів генерального середнього 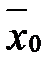 є вибірковим середнім
є вибірковим середнім  .►
.►
Метод найменших квадратів, по-перше, не потребує знання закону розподілу вибіркових даних; по-друге, достатньо добре розроблений в плані обчислювальної реалізації.






