Перевірка гіпотез про рівність середніх двох сукупностей

Нехай є дві сукупності, що характеризуються генеральними середніми 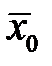та 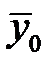і відомими дисперсіями 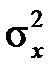та 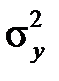. Необхідно перевірити гіпотезу Н ₀ про рівність генеральних середніх, тобто Н ₀: 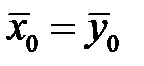. Для перевірки гіпотези Н ₀ із цих сукупностей взято дві незалежні вибірки об’ємів 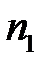та 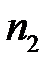, по яких знайдено середні арифметичні 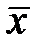та 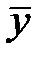і вибіркові дисперсії 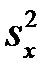та 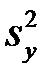. При достатньо великих об’ємах вибірки вибіркові середні 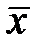та 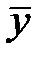мають наближено нормальний закон розподілу, відповідно 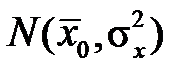і 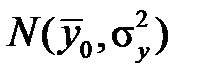. У випадку вірності гіпотези Н ₀ різниця 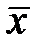- 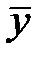має нормальний закон розподілу з математичним сподіванням

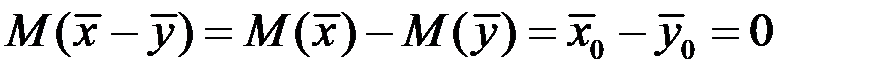
і дисперсією 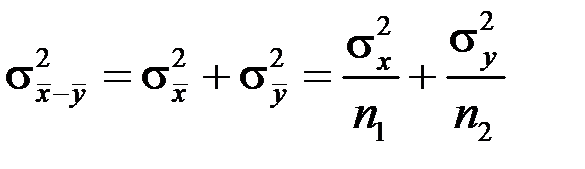. Тому при виконанні гіпотези Н ₀ статистика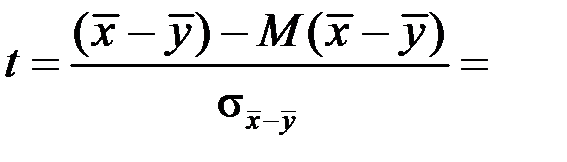 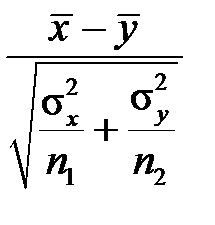має стандартний нормальний розподіл N (0;1). У випадку конкуруючої гіпотези 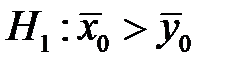(або 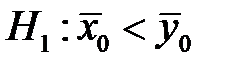) вибирають односторонню критичну область і критичне значення статистики знаходять із умови (рис.4.3); а при конкуруючій гіпотезі 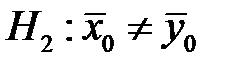вибирають двосторонню критичну область і критичне значення статистики із умови 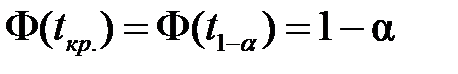(рис. 4.4).

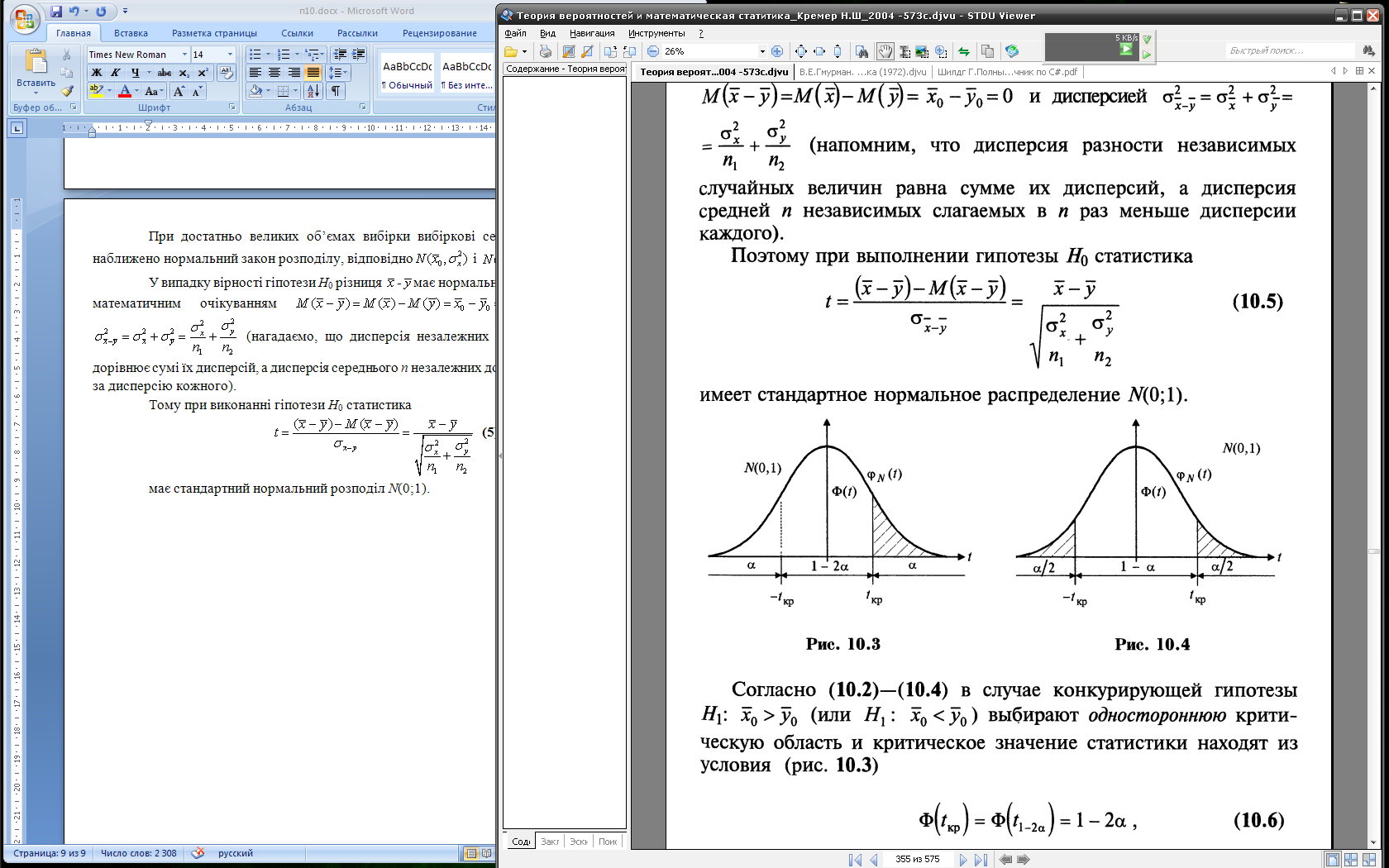
Рис. 4.3 Рис. 4.4

Якщо значення статистики t, що фактично спостерігається, більше за критичне t _кр, визначеного на рівні значущості α (за абсолютною величиною), тобто 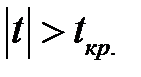, то гіпотеза Н ₀ відкидається. Якщо 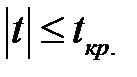, то робиться висновок, що нульова гіпотеза Н ₀ не суперечить спостереженням.

◄ Приклад 4.2 Для перевірки ефективності нової технології відібрано дві групи робітників: у першій групі чисельністю 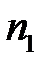=50 чоловік, де використовувалася нова технологія, вибірковий середній виробіток становив 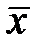=85 (виробів), у другій групі чисельністю 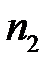=70 чоловік вибірковий середній — 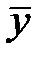=78 (виробів). Попередньо встановлено, що дисперсії виробітку в групах дорівнюють відповідно 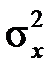=100 та 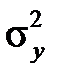=74. На рівні значущості α = 0,05 з’ясувати вплив нової технології на середню продуктивність.

Розв’язання. Гіпотеза, що перевіряється, Н ₀: 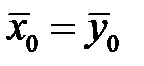, тобто середні виробітки робітників однакові по новій і старій технологіях. В якості конкуруючої гіпотези можна взяти .

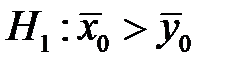Фактичне значення статистики критерію 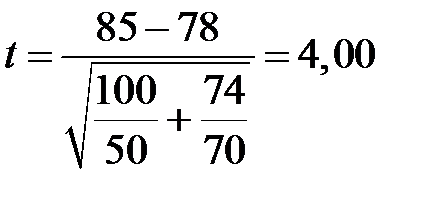. При конкуруючій гіпотезі Н ₁ критичне значення статистики знаходиться із умови 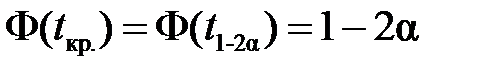, тобто 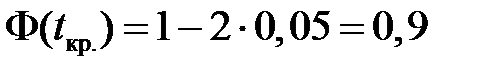, звідки по таблиці 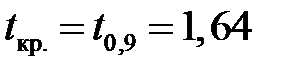, а при конкуруючій гіпотезі Н ₂ — з умови 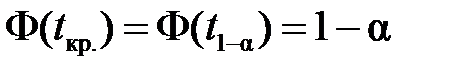, тобто 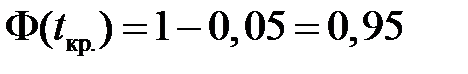, звідки по таблиці 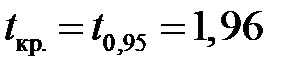. Оскільки значення t = 4,00, що фактично спостерігається, більше за критичне значення t _кр (при будь-якій із взятих конкуруючих гіпотез), то гіпотеза Н ₀ відкидається, тобто на 5%-вому рівні значущості можна зробити висновок, що нова технологія дозволяє підвищити середній виро

біток робітників.►

Будемо тепер вважати, що розподіл ознаки (випадкової величини) X та Y в кожній сукупності є нормальним. В цьому випадку, якщо дисперсії 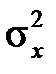та 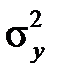відомі, то перевірка гіпотези проводиться так само, як описано вище, не тільки для великих, але й для малих по об’єму вибірок.

Якщо ж дисперсії 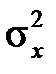та 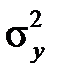невідомі, але рівні, тобто 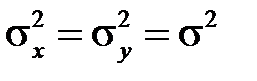, то в якості невідомої величини можна взяти їх оцінку — «виправлену» вибіркову дисперсію 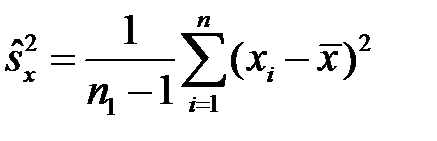або .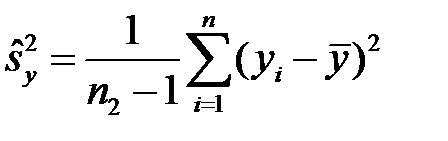

Проте «кращою» оцінкою для 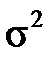буде дисперсія «змішаної» сукупності об’єму 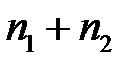, тобто

,

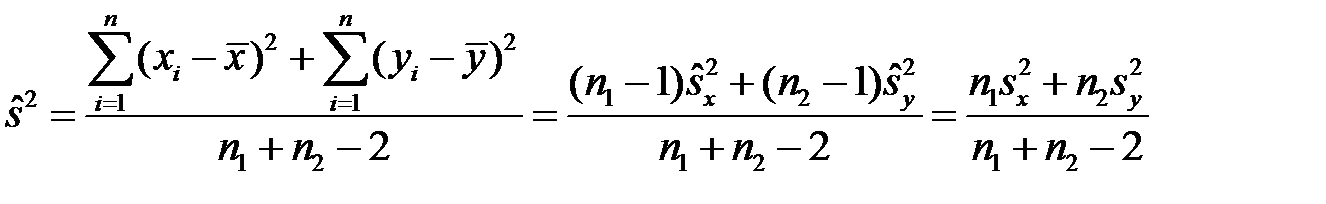а оцінкою дисперсії різниці незалежних вибіркових середніх —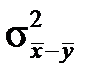

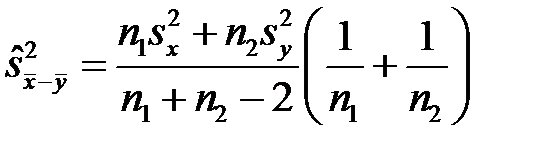(звертаємо увагу на те, що число степенів вільності 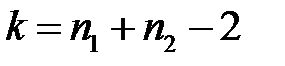на 2 менше загального числа спостережень 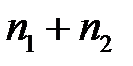, оскільки дві степені «губляться» при визначенні по вибіркових даних 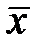та 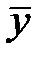). Доведено, що у випадку вірності гіпотези Н ₀ статистика

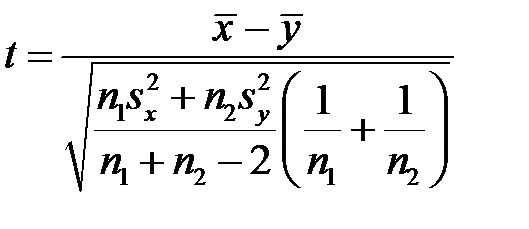має t -розподіл Стьюдента з 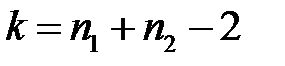степенями вільності. Тому критичне значення статистики t знаходиться за формулами 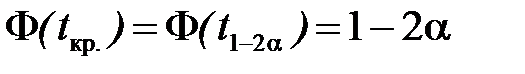і 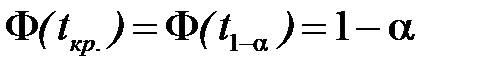в залежності від типу критичної області, в яких замість функції Лапласа Ф(t) береться функція 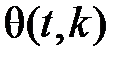для розподілу Стьюдента при числі степенів вільності 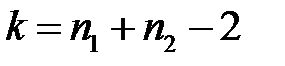, тобт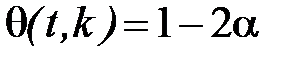о або .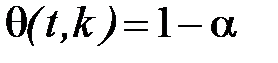

Якщо дисперсії 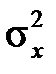та невідомі, і не вважається, що вони рівні, то статистика 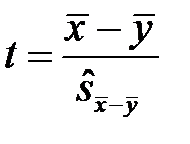також має t -розподіл Стьюдента, проте число степенів вільності, що йому відповідає, визначається наближено і більш складним чином.

◄ Приклад 4.3 Проведено дві вибірки врожаю пшениці: під час своєчасного збору врожаю і збору з певним запізненням. В першому випадку при спостереженні 8 ділянок вибіркова середня врожайність склала 16,2 ц/га, а середнє квадратичне відхилення — 3,2 ц/га; у другому випадку при спостереженні 9 ділянок ті ж характеристики дорівнювали відповідно 13,9 ц/га і 2,1 ц/га. На рівні значущості α=0,05 визначити вплив своєчасності збору врожаю на середнє значення врожайності.

Розв’язання. Гіпотеза, що перевіряється, Н ₀: 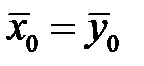, тобто середнє значення врожайності під час своєчасного збору врожаю та з певним запізненням рівні. В якості конкуруючої гіпотези беремо гіпотезу 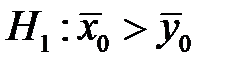, прийняття якої означає значний вплив на врожайність строків збору. Значення статистики критерію, що фактично спостерігається

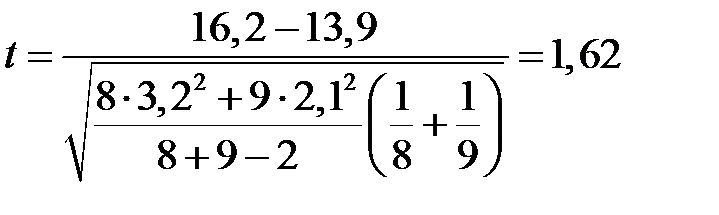
Критичне значення статистики для односторонньої області визначається

при числі степенів вільності 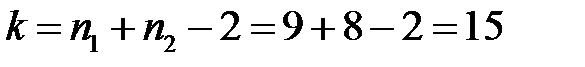із умови 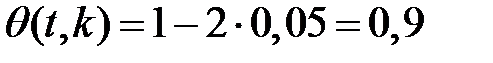, звідки по таблиці 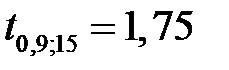. Оскільки 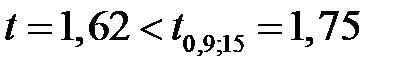, то гіпотеза Н ₀ приймається. Це означає, що вибіркові дані на 5%-вому рівні значущості не дозволяють вважати, що деяке запіз-

нення у строках збору суттєво впливають на розмір врожаю. ►