Варіаційні ряди та їх графічне зображення.
Середні величини. Показники варіації
Варіаційні ряди та їх графічне зображення
Встановлення статистичних закономірностей починається з відомостей про те, які значення прийняла в результаті спостережень ознака, що нас цікавить, яку називатимемо «випадкова величина Х».
◄Приклад 1.1 Потрібно дослідити зміну виробітку одного робітника механічного цеху у звітному році порівняно з попереднім. Одержали наступні данні щодо розподілу 100 робітників цеху за виробітком у звітному році (у відсотках до попереднього року):
►
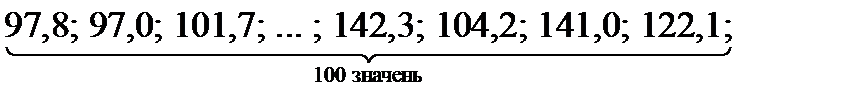Різні значення ознаки (випадкової величини Х) називаються варіантами (позначення x).
Перший крок до опрацювання наявного статистичного матеріалу – це його впорядкування: розташування варіантів в порядку зростання (спадання), тобто ранжування варіантів ряду:
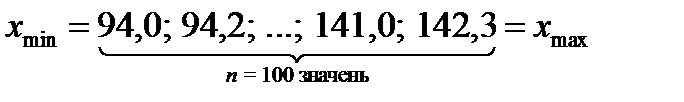
В такому вигляді вивчати виробіток робітників також не зовсім зручно, через надмірність числових даних. Через це розіб’ємо варіанти на окремі
інтервали, тобто проведемо їх групування.
Число інтервалів m слід брати не дуже великим, щоб після групуван-
ня ряд не був громіздким, і не дуже малим, щоб не втратити особливості ознаки. Рекомендована кількість інтервалів
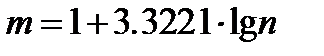(1.1)
а величина інтервалів (ширина інтервалу)
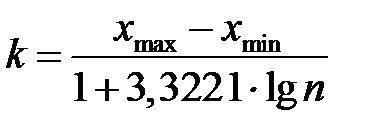(1.2)
де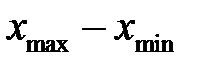 
– різниця між найбільшим і найменшим значенням ознаки.
В прикладі 1.1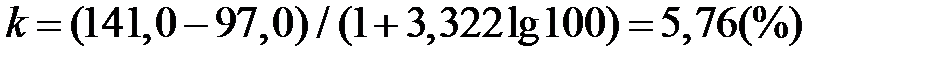 
. Візьмемо 
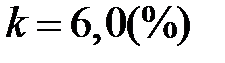. Початком першого інтервалу рекомендується обрати величину 
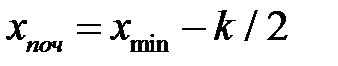. В нашому випадку 
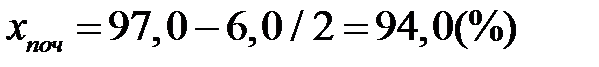. Згрупований ряд покажемо як таблицю (таблиця 1.1). Числа, що показують скільки разів зустрічались варіанти із даного інтервалу, називаються частотами (позначення 
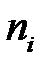), а відношення їх до загального числа спостережень – частістю або відносною частотою, тобто 
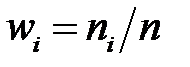. Частоти і частості називаються вагами.
Означення 1. 1 Варіаційним рядом називається ранжований в порядку зростання (чи спадання) ряд варіант із відповідними їм вагами (частотами та частостями).
Одержаний варіаційний ряд дозволяє легко виявити закономірності розподілу робітників. При вивченні варіаційних рядів використовують також поняття накопиченої частоти (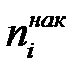
). Накопичена частота показує, скільки спостерігалось варіант зі значенням ознаки меншим за х. Відношення накопиченої частоти 
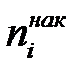до загальної кількості спостережень 
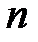назвемо накопиченою частістю 
.
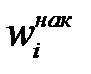Таблиця 1.1
| i | Виробіток в звітному році в відсотках до попереднього | Частота
(кількість робітників)
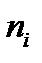
| Частість
(доля робітників)
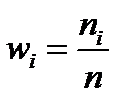
| Накопичена частота
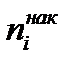
| Накопичена частість
|
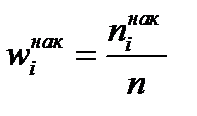
| 94,0-100,0 100,0-106,0 106,0-112,0 112,0-118,0 118,0-124,0 124,0-130,0 130,0-136,0 136,0-142,0 | 0,003 0,007 0,11 0,20 0,28 0,19 0,10 0,02 | 0,03 0,10 0,21 0,41 0,69 0,88 0,98 1,00 | |||
| ∑ | 1,00 | - | - |
Накопичену частоту (частість) для кожного інтервалу знаходять за допомогою сумування частот (частостей) всіх попередніх інтервалів, включно з даним (див. табл.1.1). Наприклад, для х = 124 накопичена частота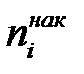 
=3 + 7 + 11 + 20 + 28 = 69, тобто 69 робітників мали виробітку меншу за 124%.
Варіаційний ряд називається дискретним, якщо будь-які його варіанти відрізняються на постійну величину, і – неперервним (інтервальним), якщо варіанти можуть відрізнятись одна від одної на яку завгодно малу величину. Так, варіаційний ряд в таблиці 1.1 - інтервальний (проценти виробітку умовно округлені до десятих). Прикладом дискретного ряду є розподіл 50 робітників механічного цеху по тарифному розряду (табл. 1.2).
Для графічного зображення варіаційних рядів найчастіше використовують полігон, гістограму, кумулятивну криву.
Таблиця 1.2
Тарифний розряд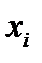 
| ∑ | ||||||
| Частота (кількість робітників)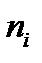
|
Полігон використовують для зображення дискретного варіаційного ряду. Він являє собою ламану, в якої кінці відрізків прямої мають координати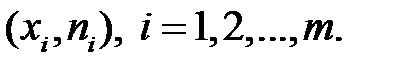 
Гістограма використовується тільки для зображення інтервальних варіаційних рядів і представляє собою ступінчасту фігуру із прямокутників з основами, що дорівнюють інтервалам значення ознаки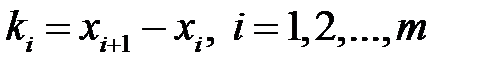 
, і висотами рівними частотам (частостям) 
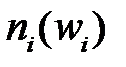інтервалів. Якщо з’єднати середини верхніх основ прямокутників відрізками прямої то можна одержати полігон розподілу.
Кумулятивна крива (кумулята) – крива накопичених частот (частостей). Для дискретного ряду кумулята представляє ламану, з’єднану точками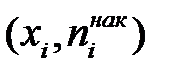 
або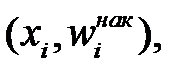 
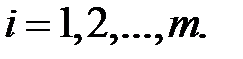Для інтервалів варіаційного ряду ламана починається з точки, абсциса якої дорівнює початку першого інтервалу, а ордината – накопиченій частоті (частості), що дорівнює нулю. Інші точки цієї ламаної відповідають кінцям інтервалів.
Означення 1.2 Емпіричною функцією розподілу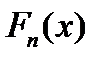 
називається відносна частота (частість) того, що ознака (випадкова величина Х) прийме
значення, менше заданого х, тобто:
.
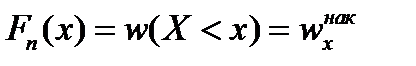Тобто, для даного х емпірична функція розподілу представляє нако-
пичену частість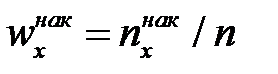 
.
◄ Приклад 1.2 Побудувати полігон (гістограму), кумуляту і емпіричну функцію розподілу робочих:
а) по тарифному розряду за даними табл. 1.2;
б) по виробітці за даними табл. 1.1.
Розв’язання. На рисунках 1.1 і 1.2 зображені полігон (гістограма), кумулята і емпірична функція розподілу для дискретного (табл. 1.2) і інтревального (табл. 1.1) варіаційних рядів відповідно. ►
Для інтервального варіаційного ряду (табл. 1.1) маємо тільки фун-
кцію розподілу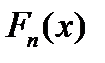 
на кінцях інтервалу (остання графа табл. 1.1).
Тому для графічного зображення варто її довизначити, з’єднавши точки графіка, що відповідають кінцям інтервалів, відрізками прямої. В результаті одержана ламана співпадає із кумулятою (див. рис. 1.2,б). Варіаційний ряд є статистичним аналогом (реалізацією) розподілу ознаки (випадкової величини Х). В цьому значенні полігон (гістограма) аналогічний кривій розподілу, а емпірична функція розподілу – функції розподілу випадкової величини Х.
На практиці, в більшості випадків, достатньо знати тільки зведені характеристики варіаційних рядів: середні; характеристики мінливості (варіації) та ін. Розрахунок статистичних характеристик є другим після групування даних етапом спостережень.
Середні величини
Середні величини характеризують значення ознаки, навколо якої концентруються спостереження. Найбільш поширеною із середніх величин є середнє арифметичне.
Означення 1.3Середнім арифметичним варіаційного ряду називається сума добутків всіх варіант на відповідні частоти, поділена на суму частот:
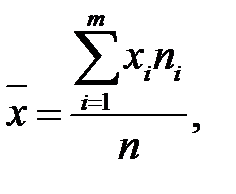(1.3)
де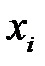 
- варіанти дискретного ряду або середини інтервалів інтервального варіаційного ряду; 
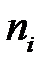- відповідні їм частоти; 
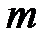- кількість варіант, що не повторюються, або кількість інтервалів: 
.
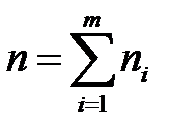Очевидно, що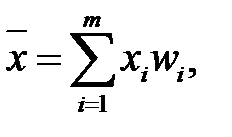 
де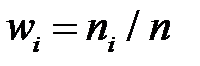 
- частоти варіант або інтервалів.
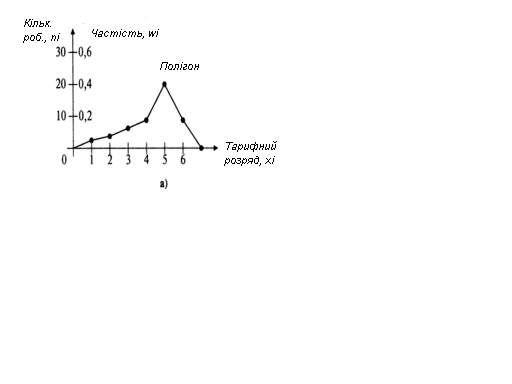
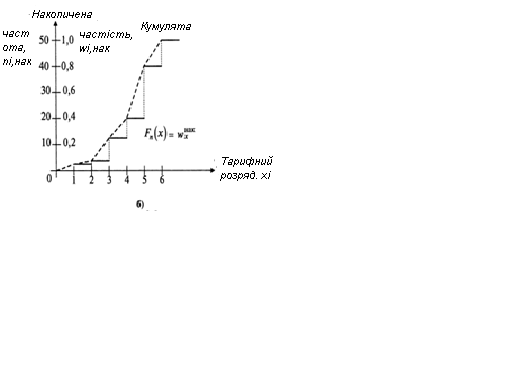
Рис. 1.1
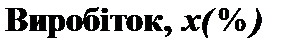
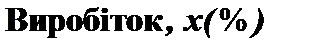
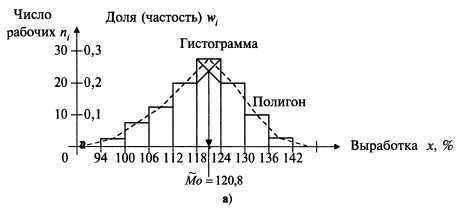
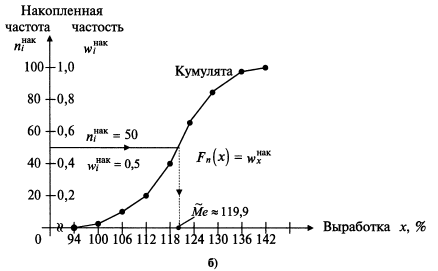
Рис.1.2
◄ Приклад 1.3 Знайти середній виробіток робітників за даними табл.1.1.
Розв’язання. За формулою (1.3) для інтервального варіаційного ряду
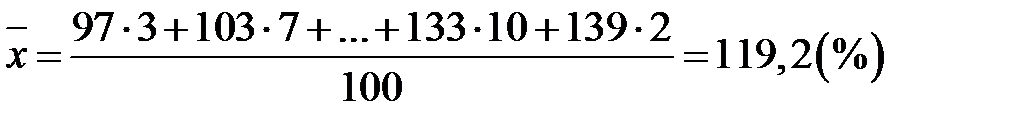
де числа 97, 103,…, 133, 139 – середини відповідних інтервалів. Для незгрупованого ряду всі частоти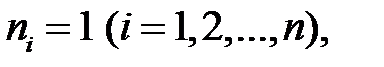 
а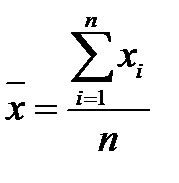 
є «непов-ним» середнім арифметичним.►
Розглянемо основні властивості середнього арифметичного, аналогічні властивостям математичного сподівання випадкової величини:
1. Середнє арифметичне сталої рівне самій сталій..
2. Якщо усі варіанти збільшити (зменшити) в одне і те ж число раз, то середнє арифметичне збільшиться (зменшиться) у стільки ж разів: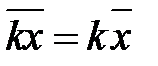 
або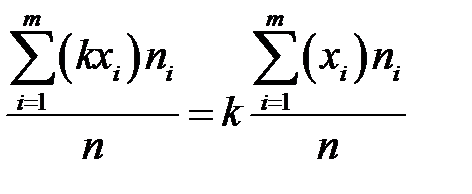 
.
3. Якщо усі варіанти збільшити (зменшити) на одне і те саме число, то середнє арифметичне збільшиться (зменшиться) на це число:
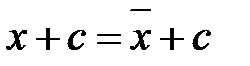або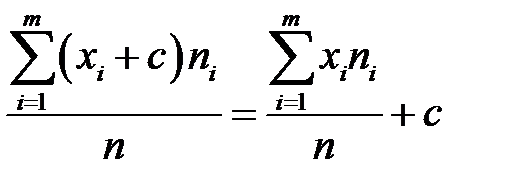 
.
4. Середнє арифметичне відхилень варіантів від середнього арифметичного дорівнює нулю: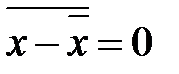 
або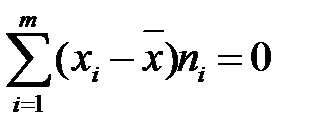 
.
5. Середнє арифметичне алгебраїчної суми декількох ознак дорівнює такій самій сумі середніх арифметичних цих ознак:
.
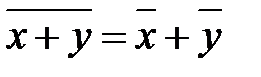6. Якщо ряд складається з декількох груп, загальне середнє дорівнює середньому арифметичному групових середніх, причому вагами є об'єми груп: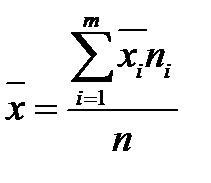 
.
При розв’язанні практичних задач можуть застосовуватися і інші форми середнього, які можна отримати з середнього степеневого к-го порядку
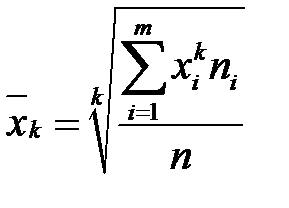, де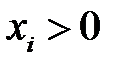 
.
Зауважимо, що при k = 1отримуємо формулу середнього арифметичного. При інших значеннях k отримуємо формули:
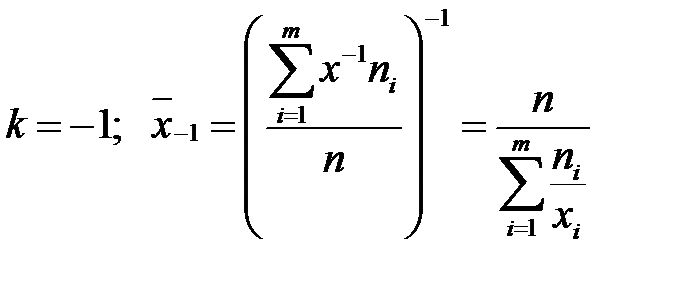- середнє гармонійне;
; 
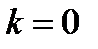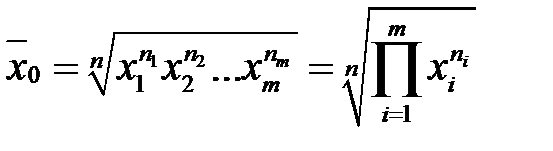- середнє геометричн е.
Окрім розглянутих середніх величин, що називаються аналітичними, в статистичному аналізі застосовують структурні, або порядкові, середні.
З них найчастіше застосовуються медіана і мода.
Означення 1.4 Медіаною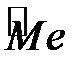 
варіаційного ряду називається значення ознаки, що припадає на середину ранжируваного ряду спостережень.
Для дискретного варіаційного ряду з непарною кількістю членів медіана дорівнює центральній варіанті, а для ряду з парним - півсумі двох центральних варіант.
◄Приклад 1.4. Знайти медіану розподілу робітників по тарифному розряду за даними таблиці 1.2.
Розв’язання. n =50 –парне, отже, центральних варіант дв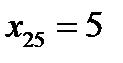і: 
і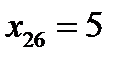 
. Отже 
.►
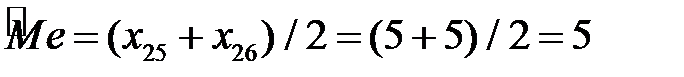Для інтервального варіаційного ряду знаходиться медіанний інтервал, на який припадає середина ряду, а значення медіани на цьому інтервалі знаходять за допомогою лінійної інтерполяції. Зауважимо, що медіана може бути приблизно знайдена за допомогою кумуляты як значення ознаки, для якої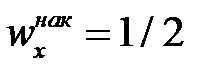 
.
Придатність медіани як міри центральної тенденції полягає в тому, що на неї не впливає зміна крайніх членів варіаційного ряду, якщо будь-який із них, менший медіани, залишається меншим від неї, а будь-який, більший медіани, продовжує бути більшим від неї. Медіану краще застосовувати (ніж середнє арифметичне) для ряду, у якого крайні варіанти в порівнянні з іншими виявилися надмірно великими або малими.
Означення 1.5 Модою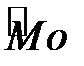 
варіаційного ряду називається варіанта, якій відповідає найбільша частота.
Наприклад, для варіаційного ряду табл. 1.2 мода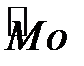 
= 5, оскільки цій варіанті відповідає найбільша частота 
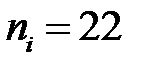. Для інтервального ряду знаходиться модальний інтервал, що має найбільшу частоту, а значення моди на цьому інтервалі визначають за допомогою лінійної інтерполяції. Проте, простіше моду можна знайти графічним шляхом за допомогою гістограми. Особливість моди як міри центральної тенденції полягає в тому, що вона не змінюється при зміні крайніх членів ряду, тобто має певну стійкість до варіації.
◄Приклад 1.5 Знайти медіану і моду розподілу робітників по виробітку за даними табл. 1.1
Розв’язання. На рис. 1.2 проведемо горизонтальну пряму у = 0,5 (або n =50), що відповідає накопиченій частості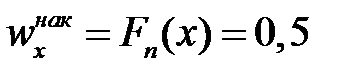 
(або накопиченій частоті 
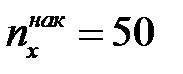), до перетину з графіком емпіричної функції розподілу (чи кумуляти). Абсциса точки перетину і буде медіаною варіаційного ряду: 
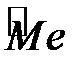=119,9(%).
На гістограмі розподілу (рис. 1.2) знаходимо прямокутник з найбільшою частістю. Сполучаючи відрізками прямих вершини цього прямокутника із відповідними вершинами двох сусідніх прямокутників (див. рис. 1.2), отримаємо точку перетину цих відрізків (діагоналей), абсциса якої і буде модою варіаційного ряду: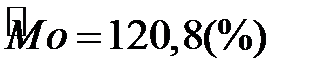 
.►
Показники варіації
Середні величини, розглянуті вище, не відображають мінливості (варіації) значень ознаки.
Найпростішим (і дуже наближеним) показником варіації є варіаційний розмах R, рівний різниці між найбільшою і найменшою варіантами ряду: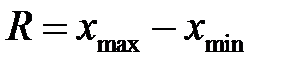 
.
Середнім лінійним відхиленням варіаційного ряду називається середнє арифметичне абсолютних величин відхилень варіант від їх середнього арифметичного:
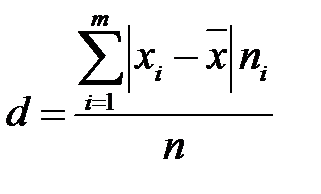
Означення 1.6 Дисперсією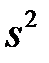 
варіаційного ряду називається середнє арифметичне квадратів відхилень варіант від їх середнього арифметичного:
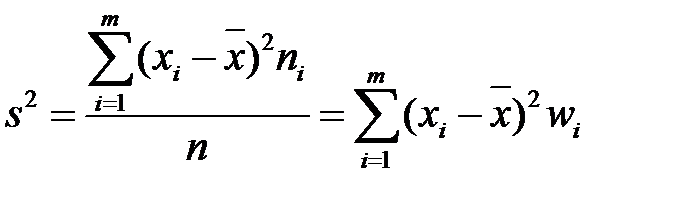(1.4)
Для незгрупованого ряду (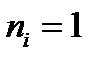
) із формули (1.4) маємо:
.
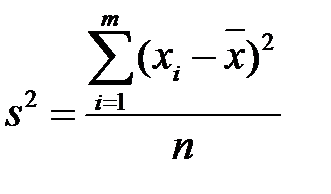Дисперсію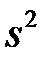 
називають емпіричною або вибірковою, підкреслюючи,
що вона (на відміну від дисперсії випадкової величини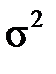 
) знаходиться за
дослідними або статистичними даними.
Бажано в якості міри варіації (розсіювання) мати характеристику, яка
виражається в тих самих одиницях, що і значення ознаки. Такою характеристикою є середнє квадратичне відхилення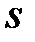 
- арифметичне значення кореня квадратного з дисперсії
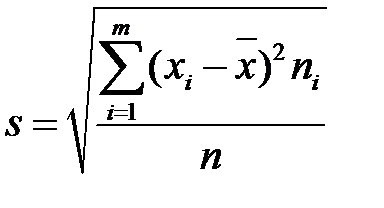. (1.5)
В деяких випадках використовують таку характеристику, як коефіцієнт варіації, що дорівнює відсотковому відношенню середнього квадратичного відхилення до середнього арифметичного:
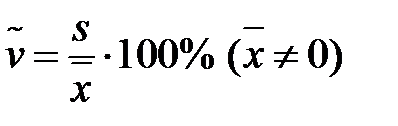(1.6)
Якщо коефіцієнт варіації ознаки, набуває тільки позитивних значень, є
високим (наприклад, більше 100%), то, як правило, це свідчить про неоднорідність значень ознаки.
Основні властивості дисперсії, аналогічні властивостям дисперсії випадкової величини:
1. Дисперсія сталої дорівнює нулю.
2. Якщо усі варіанти збільшити (зменшити) в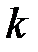 
разів, то дисперсія збільшиться (зменшиться) в 
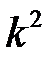разів:
.
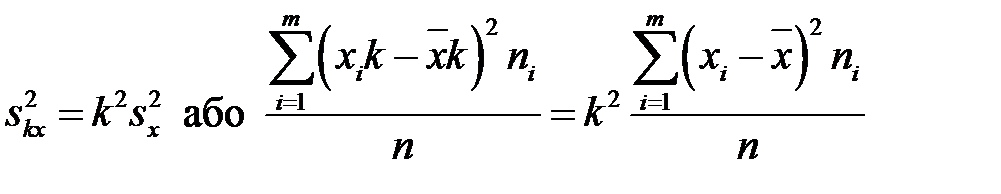3. Якщо всі варіанти збільшити (зменшити) на одне і те саме число, то дисперсія не зміниться:
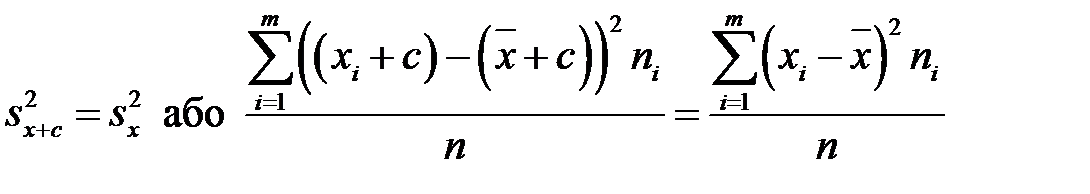
4. Дисперсія дорівнює різниці між середнім арифметичним квадратів варіант і квадратом середнього арифметичного:
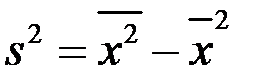
5. Якщо ряд складається з декількох груп спостережень, то загальна дисперсія дорівнює сумі середнього арифметичного групових дисперсій і міжгрупової дисперсії (правило додавання дисперсій):
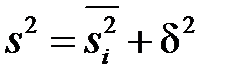
де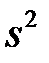 
- загальна дисперсія (дисперсія всього ряду);
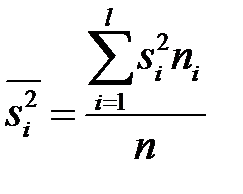- середня арифметична групових дисперсій,
де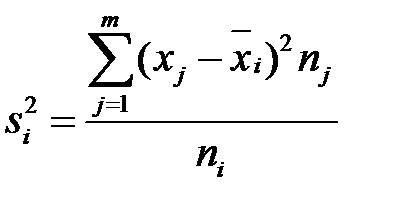 
; 
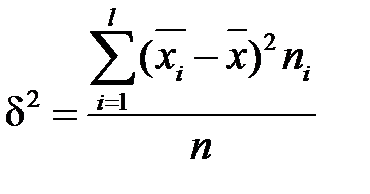- міжгрупова дисперсія.
◄Приклад 1.6 Обчислити дисперсію, середнє квадратичне відхилення і коефіцієнт варіації розподілу робітників по виробітці за даними табл. 1.1.
Розв’язання. В прикладі 1.3 було одержано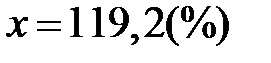 
.
З означення дисперсії:
.
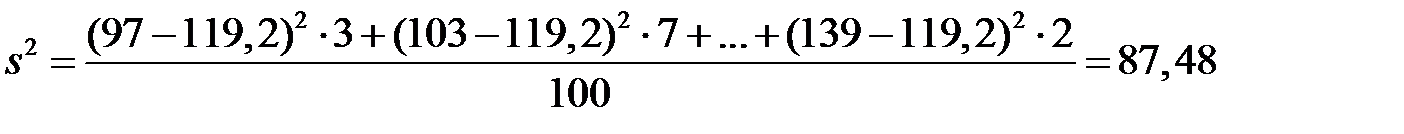Середнє квадратичне відхилення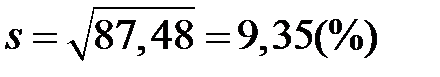 
;
коефіцієнт варіації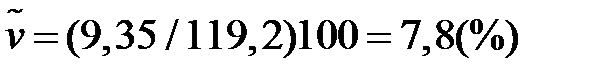 
.►
◄Приклад 1.7 Є наступні дані про середні та дисперсії заробітної платні двох груп робітників (таблиця 1.3). Знайти загальну дисперсію
розподілу робітників за заробітною платнею і коефіцієнт варіації.
Розв’язання. Знайдемо загальне середнє
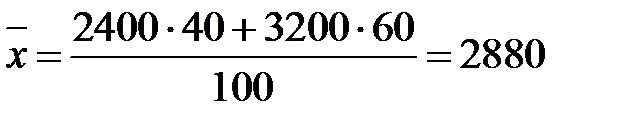
Знайдемо середнє групових дисперсій
.
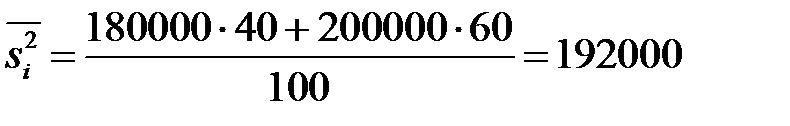Знайдемо міжгрупову дисперсію:
.
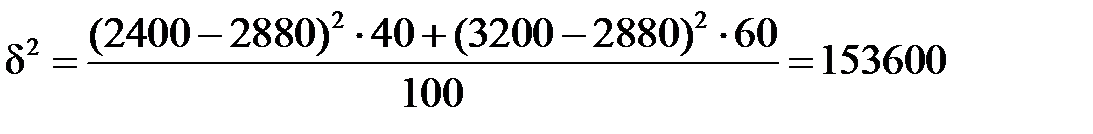Таблиця 1.3
| Група робітників | Кількість робітників | Середня зарплатня одного робітника | Дисперсія зарплатні |
| Працюють на одному станку | 180 000 | ||
| Працюють на двох станках | 200 000 |
Знайдемо загальну дисперсію:
.
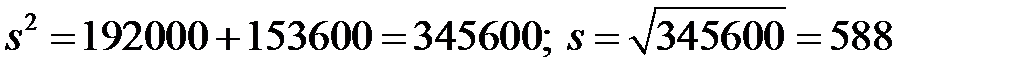Коефіцієнт варіації:
.►
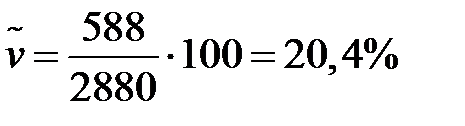