Завдання побудови довірчого інтервалу для генерального середнього може бути розв’язане, якщо в генеральній сукупності дана ознака має нормальний розподіл.
Теорема 3. 2 Якщо ознака (випадкова величина) X має нормальний закон розподілу з параметрами M(x)= 
, 
, тобто 
, то вибіркове середнє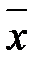 
при будь-якому n (а не тільки при 
) має нормальний закон розподілу 
.
Доведення. Якщо у випадку великих вибірок (при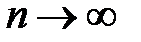 
) із будь-яких
генеральних сукупностей нормальність розподілу 
була зумовлена сумуванням великого числа однаково розподілених випадкових величин 
(теорема Ляпунова), то у випадку малих вибірок, отриманих із нормальної генеральної сукупності, нормальність розподілу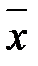 
випливає з того, що розподіл суми (композиція) будь–якого числа нормально розподілених випадкових величин має нормальний розподіл. Формули числових характеристик для 
отримані в теоремі 2.3 (розділ 2).
Таким чином, якщо б була відома генеральна дисперсія 
, то довірчий інтервал можна було б побудувати аналогічно вище зазначеному і при малих n. Зауважимо, що при цьому нормоване відхилення середнього 
має стандартний нормальний розподіл N (0;1). Справді, використовуючи властивості математичного сподівання і дисперсії, отримаємо:
,
Щоправда, на практиці майже завжди генеральна дисперсія 
(як і оцінювана генеральне середнє 
) невідома. Якщо замінити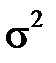 
її «найкращою» оцінкою по вибірці, а саме «виправленою» вибірковою дисперсією 
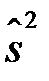, то більшу привабливість має розподіл вибіркової характеристики (статистики) 
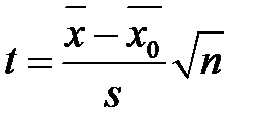або розподіл статистики 
. Представимо статистику t в вигляді: 
. Чисельник виразу має стандартний нормальний розподіл N (0;1). Можна показати, що випадкова величина 
має 
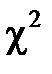- розподіл з k=n -1 степенями вільності. Таким чином, статистика t має t -розподіл Стьюдента з k=n -1 степенями вільності. Вказаний розподіл не залежить від невідомих параметрів розподілу випадкової величини X, а залежить тільки від числа k, яке називається числом степенів вільності. Число степенів вільності k визначається як загальне число n спостережень (варіант) випадкової величини X мінус число рівнянь l, що зв’язують ці спостереження, тобто k = n - l.
Так, наприклад, для розподілу статистики 
число степенів вільності k=n- 1, бо один степінь «губиться» при визначенні вибіркового середнього 
(n спостережень пов’язані одним рівнянням 
). Знаючи t -розподіл Стьюдента, можна знайти таке критичне значення 
, що ймовірність того, що статистика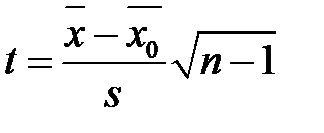 
не перевищить величину (за абсолютною величиною), рівна 
:
.
Функція 
, де 
- густина ймовірностей
t -розподілу Стьюдента при числі степенів вільності k, табульована. Ця функція аналогічна функції Лапласа Ф(t), але на відміну від неї є функцією двох змінних: t і k = n -1. При 
функція 
нескінченно наближається до функції Лапласа Ф(t). Формула довірчої ймовірності для малої вибірки може бути подана в рівносильному вигляді:
,
де 
- гранична похибка малої вибірки. Довірчий інтервал для генерального середнього знаходиться за формулою:
.
◄ Приклад 3.6 Для контролю строку служби електроламп з великої партії було відібрано 17 електроламп. В результаті дослідів виявилось, що середній строк служби відібраних ламп дорівнює 980 год., а середнє квадратичне відхилення їх строку служби - 18год. Необхідно знайти:
а) ймовірність того, що середній строк служби ламп у всій партії відрізняється від середнього строку служби відібраних для дослідів ламп не більше ніж на 8год. (за абсолютною величиною); б) межі, в яких із ймовірністю 0,95 знаходиться середній строк служби ламп у всій партії.
Розв’язання. Маємо за умовою n =20, 
(год.), s =18год.
а) знаючи граничну похибку малої вибірки 
=8(год.), знайдемо : 
. Тепер шукана довірча ймовірність 
, (
знаходимо за таблицею значень 
при числі степенів вільності k =16). Отже, ймовірність того, що розбіжність середніх строків служби електроламп у вибірці і у всій партії не перевищить 8 год. (за абсолютною величиною), дорівнює 0,906.
б) Беручи до уваги, що 
і (за таблицею) 
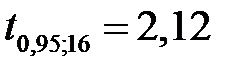, знай-
демо граничну похибку малої вибірки 
(год.). Тепер шуканий довірчий інтервал 
або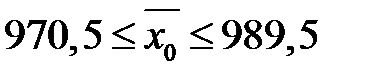 
(год.), тобто з надійністю 0,95 середній строк служби електроламп в партії знаходиться в проміжку від 970,5 до 989,5 год.►
