Нехай розподіл ознаки (випадкової величини) X в генеральній сукупності є нормальним 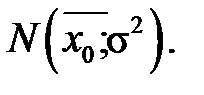 Будемо думати, що математичне сподівання
Будемо думати, що математичне сподівання 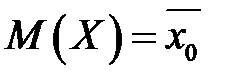 (генеральне середнє) відоме. Тоді вибіркова дисперсія повторної вибірки
(генеральне середнє) відоме. Тоді вибіркова дисперсія повторної вибірки 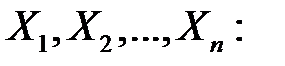
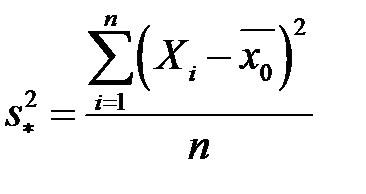 (її не варто плутати з вибірковою дисперсією
(її не варто плутати з вибірковою дисперсією 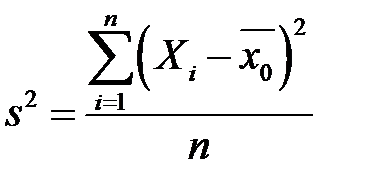 і «виправленою» вибірковою
і «виправленою» вибірковою
Рис. 3.3
дисперсією 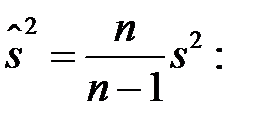 якщо
якщо 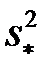 характеризує варіацію значень ознаки відносно генерального середнього
характеризує варіацію значень ознаки відносно генерального середнього 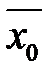 , то
, то 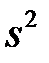 і
і 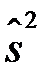 - відносно вибіркового середнього
- відносно вибіркового середнього 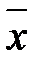 ). Розглянемо статистику
). Розглянемо статистику 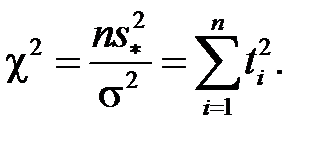
Враховуючи, що 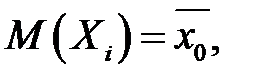
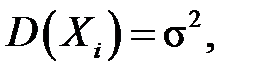
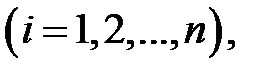 неважко показати, що
неважко показати, що 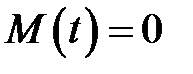 і
і 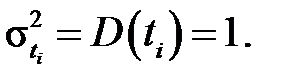 Розподіл суми квадратів n незалежних випадкових величин
Розподіл суми квадратів n незалежних випадкових величин 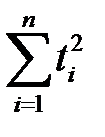 , кожна з яких має стандартний нормальний розподіл
, кожна з яких має стандартний нормальний розподіл 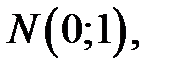 являє собою
являє собою 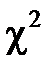 з
з 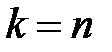 степенями вільності. Розподіл
степенями вільності. Розподіл 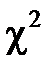 не залежить від невідомих параметрів випадкової величини X,
не залежить від невідомих параметрів випадкової величини X,
а залежить лише від числа степенів вільності k.
Густина ймовірності розподілу 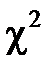 має складний вигляд, і її інтегрування є складним. Складено таблиці для обчислення ймовірності того, що випадкова величина (яка має
має складний вигляд, і її інтегрування є складним. Складено таблиці для обчислення ймовірності того, що випадкова величина (яка має 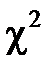 -розподіл з k степенями вільності) перевищить деякі критичні значення
-розподіл з k степенями вільності) перевищить деякі критичні значення 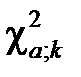 , тобто
, тобто 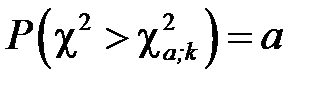 . В практиці вибіркового спостереження математичне сподівання
. В практиці вибіркового спостереження математичне сподівання 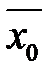 , як правило, невідоме, і доводиться мати справу не з
, як правило, невідоме, і доводиться мати справу не з 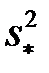 , а з
, а з 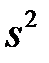 . Якщо
. Якщо 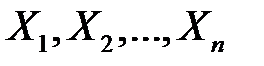 - повторна вибірка із нормально розподіленої генеральної сукупності, то випадкова величина
- повторна вибірка із нормально розподіленої генеральної сукупності, то випадкова величина 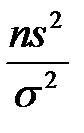 (або
(або 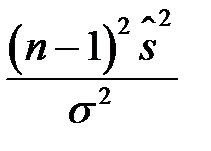 ) має розподіл
) має розподіл 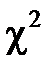 з
з 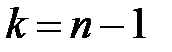 степенями вільності. Тому для заданої довірчої ймовірності
степенями вільності. Тому для заданої довірчої ймовірності 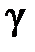 можна записати:
можна записати: 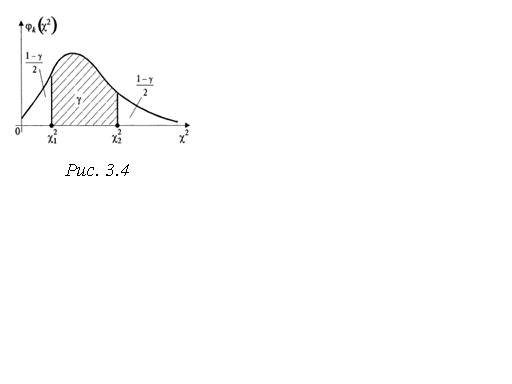
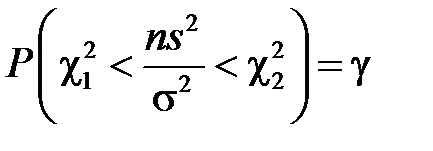 (графічно це площина під кривою розподілу між
(графічно це площина під кривою розподілу між 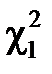 і
і 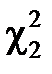 , див. рис. 3.4). Очевидно, що значення
, див. рис. 3.4). Очевидно, що значення 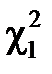 і
і 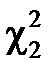 визначаються неоднозначно при одному і тому ж значенні заштрихованої площі, яка дорівнює
визначаються неоднозначно при одному і тому ж значенні заштрихованої площі, яка дорівнює 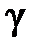 . Зазвичай
. Зазвичай 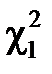 і
і 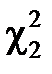 вибирають таким чином, щоб ймовірності подій
вибирають таким чином, щоб ймовірності подій 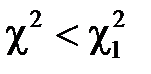 і
і 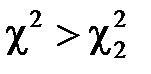 були однаковими, тобто
були однаковими, тобто
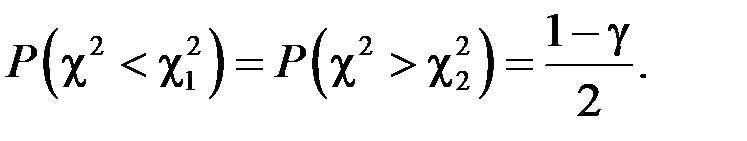
Перетворивши подвійну нерівність 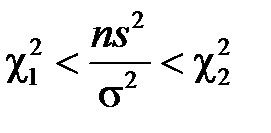 до рівносильного вигляду
до рівносильного вигляду 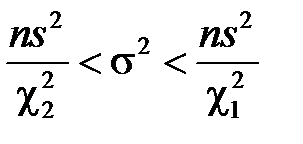 , отримаємо формулу довірчої ймовірності для генеральної дисперсії:
, отримаємо формулу довірчої ймовірності для генеральної дисперсії: 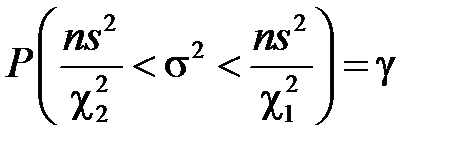 , а для середнього квадратичного відхилення:
, а для середнього квадратичного відхилення: 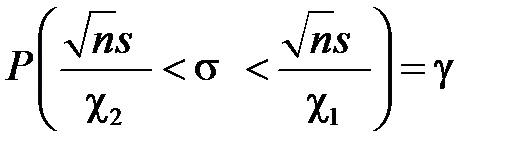 .
.
При використанні таблиць значень 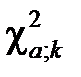 , отриманих з рівності
, отриманих з рівності 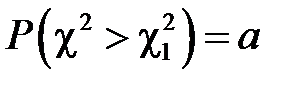 , необхідно врахувати, що
, необхідно врахувати, що 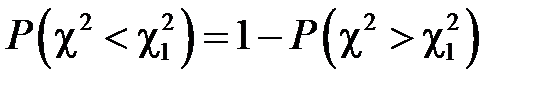 ,
,
тому умова 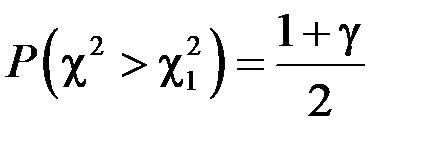 рівносильна умові
рівносильна умові 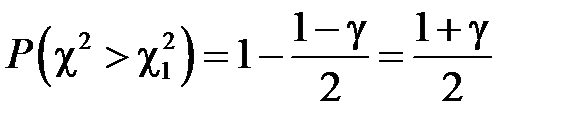 . Таким чином, значення
. Таким чином, значення 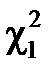 і
і 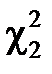 знаходимо по таблиці із рівностей:
знаходимо по таблиці із рівностей: 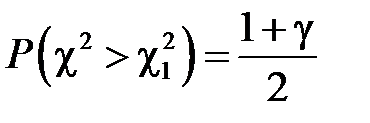 ,
, 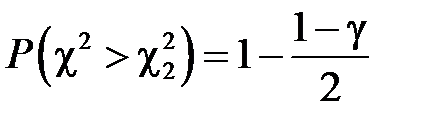 .
.
Тобто при 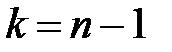
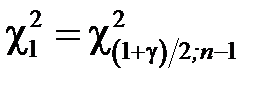 ,
, 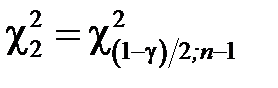 .
.
◄Приклад 3.8 На основі вибіркових спостережень продуктивності праці 20 робітниць було встановлено, що середнє квадратичне відхилення добового виробітку складає 15 м тканини в годину. Вважаючи, що продуктивність роботи робітниць має нормальний розподіл, знайти межі, в яких з надійністю 0,9 находяться генеральна дисперсія і середнє квадратичне відхилення добового виробітку робітниці.
Розв’язання. Маємо 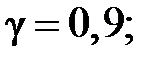
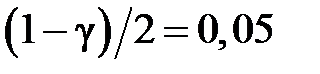 ;
; 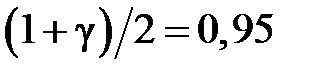 .
.
При числі степенів свободи 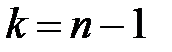 =20-1=19 визначимо
=20-1=19 визначимо 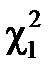 і
і 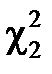 за таблицею значень для
за таблицею значень для 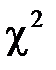 - розподілу:
- розподілу:
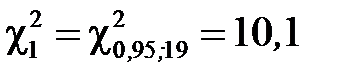 і
і 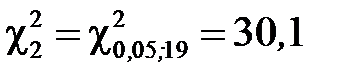 . Тоді довірчий інтервал для
. Тоді довірчий інтервал для  можна записати у вигляді:
можна записати у вигляді: 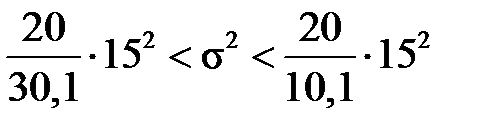 або
або 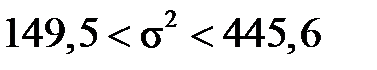 ,
,
і для  :
: 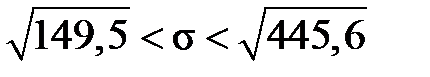 або
або 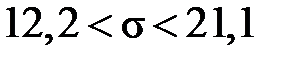
 .
.
Отже, з надійністю 0,9 дисперсія добового виробітку робітниць знаходиться в межах від 149,5 до 445,6, а її середнє квадратичне відхилення – від 12, 2 до 21,1 метрів тканини за годину.►
Зауваження. Таблиця значень 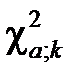 складена при числі степенів вільності
складена при числі степенів вільності 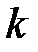 від 1 до 30. При
від 1 до 30. При 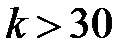 можна вважати, що випадкова величина
можна вважати, що випадкова величина 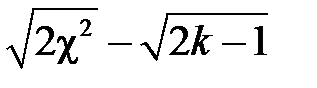 має стандартний нормальний розподіл N (0;1). Тому для визначення
має стандартний нормальний розподіл N (0;1). Тому для визначення 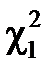 і
і 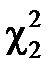 необхідно записати, що
необхідно записати, що 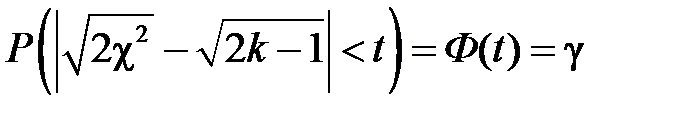 , звідки
, звідки 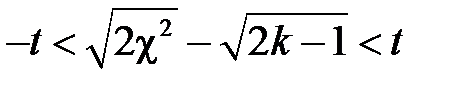 , і після перетворень:
, і після перетворень: 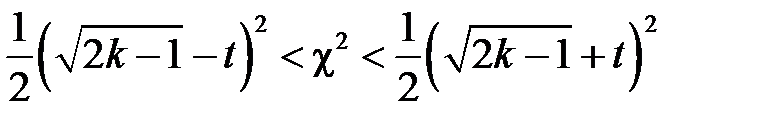 . Таким чином, при обчисленні довірчого інтервалу при
. Таким чином, при обчисленні довірчого інтервалу при 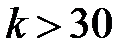 потрібно вважати
потрібно вважати 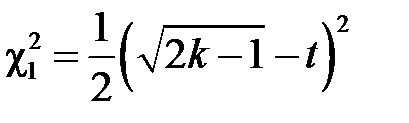 ,
, 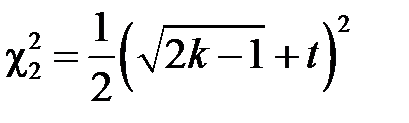 , де Ф (
, де Ф ( )=
)= 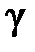 .
.
Контрольні питання
1. В чому полягає різниця між повторною і безповторною вибірками?
2. Що таке оцінка параметру розподілу?
3. Для чого використовують нерівність Рао-Крамера-Фреше?
4. Як побудувати довірчий інтервал?
5. Які переваги і недоліки методу найменших квадратів знаходження оцінок?




