Нехай із генеральної сукупності об’єму N відібрана випадкова вибірка 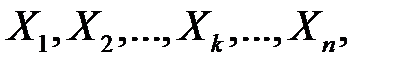 де
де 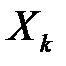 - випадкова величина, що виражає значення ознаки y k- го елемента вибірки
- випадкова величина, що виражає значення ознаки y k- го елемента вибірки 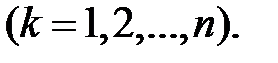 Знайдемо «найкращу»
Знайдемо «найкращу»
оцінку для генерального середнього.
Розглянемо в якості такої можливої оцінки вибіркове середнє 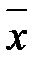 (згадаємо, що в прикладі 2.4саме
(згадаємо, що в прикладі 2.4саме 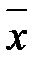 виявилось оцінкою методом найменших квадратів для
виявилось оцінкою методом найменших квадратів для 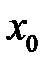 ), тобто
), тобто 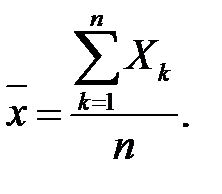
а) Вибірка повторна
Закон розподілу для кожної випадкової величини 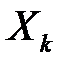
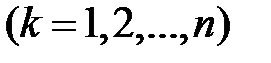 має вигляд
має вигляд
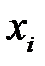
| 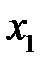
| 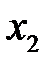
| ... | 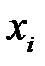
| ... | 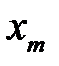
| ||
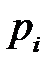
| 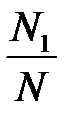
| 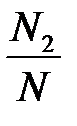
| ... | 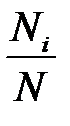
| ... | 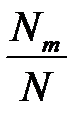
|
Дійсно, ймовірність того, що 1-й відібраний у вибірку елемент має значення ознаки 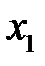 , згідно із класичним означенням ймовірності дорівнює
, згідно із класичним означенням ймовірності дорівнює 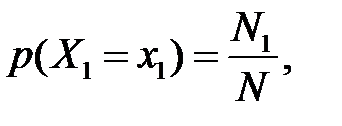 оскільки
оскільки 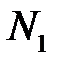 елементів мають значення ознаки
елементів мають значення ознаки 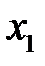 . Оскільки вибірка повторна, і кожен відібраний і досліджений елемент повертається у вихідну сукупність, відновлюючи кожен раз її початковий склад і об’єм, то ймовірність
. Оскільки вибірка повторна, і кожен відібраний і досліджений елемент повертається у вихідну сукупність, відновлюючи кожен раз її початковий склад і об’єм, то ймовірність 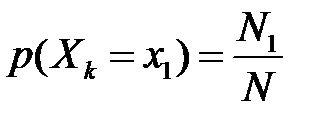 для будь-якого елемента вибірки. Аналогічно,
для будь-якого елемента вибірки. Аналогічно, 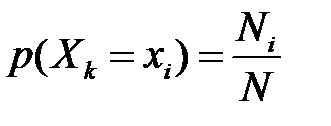 для
для 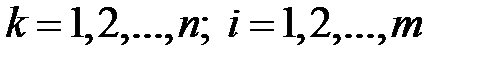 і запевняємось у тому, що закон розподілу кожної випадкової величини
і запевняємось у тому, що закон розподілу кожної випадкової величини 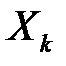 один і той самий. Випадкові величини
один і той самий. Випадкові величини 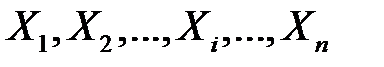 незалежні, оскільки незалеж- ними є будь-які події
незалежні, оскільки незалеж- ними є будь-які події 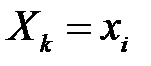
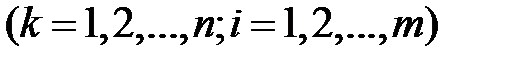 та їх комбінації.
та їх комбінації.
Знайдемо числові характеристики випадкової величини 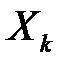 :
:
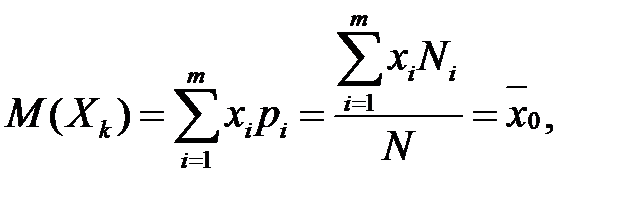 (2.9)
(2.9)
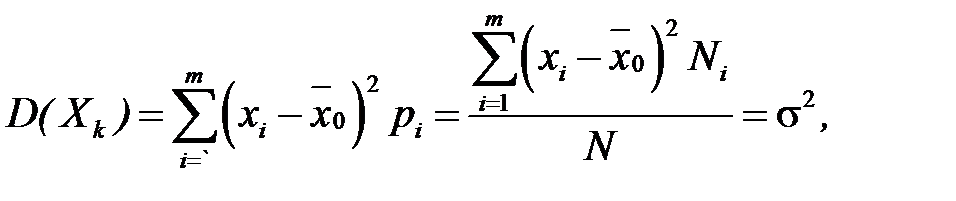 (2.10)
(2.10)
тобто математичне сподівання і дисперсія кожної випадкової величини
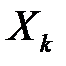 - це відповідно генеральне середнє і генеральна дисперсія.
- це відповідно генеральне середнє і генеральна дисперсія.
Теорема 2.3 Вибіркове середнє 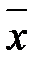 повторної вибірки є незміщеною і спроможною оцінкою генерального середнього
повторної вибірки є незміщеною і спроможною оцінкою генерального середнього 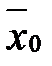 , причому
, причому
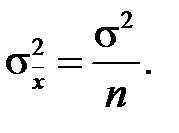 (2.11)
(2.11)
Доведення. Доведемо спочатку незміщеність оцінки. Знайдемо математичне сподівання вибіркового середнього 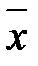 , враховуючи ( 2.9 ):
, враховуючи ( 2.9 ):
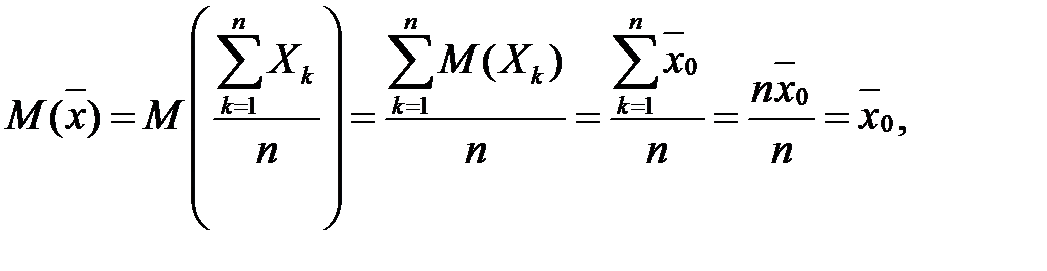
тобто 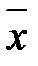 - незміщена оцінка для
- незміщена оцінка для 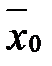 . Знайдемо дисперсію вибіркового середнього
. Знайдемо дисперсію вибіркового середнього 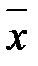 , враховуючи ( 2.10 ) і те, що
, враховуючи ( 2.10 ) і те, що 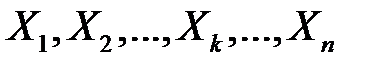 - незалежні
- незалежні
випадкові величини:

Залишилось довести спроможність оцінки 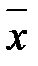 , яка випливає безпосередньо із теореми Чебишова:
, яка випливає безпосередньо із теореми Чебишова: 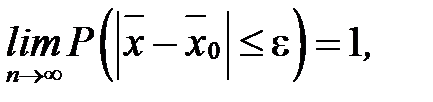 або
або 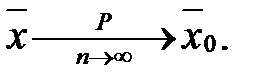
Б) Вибірка безповторна
У цьому випадку випадкові величини 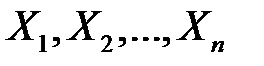 будуть залежними. Розглянемо, наприклад, події
будуть залежними. Розглянемо, наприклад, події  і
і 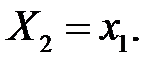 Тепер ймовірність
Тепер ймовірність 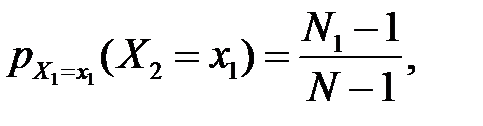 оскільки відібраний елемент (у випадку безповторної вибірки) у вихідну сукупність не повертається, то в ній залишається всього N – 1елементів, з яких зі значенням ознаки:
оскільки відібраний елемент (у випадку безповторної вибірки) у вихідну сукупність не повертається, то в ній залишається всього N – 1елементів, з яких зі значенням ознаки: 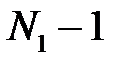 . Ця імовірність
. Ця імовірність 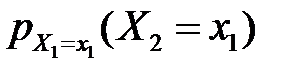 не дорівнює
не дорівнює 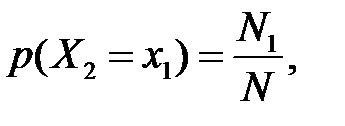 тобто події
тобто події 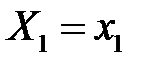 і
і 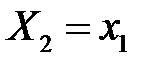 залежні. Аналогічно будуть залежними будь-які події
залежні. Аналогічно будуть залежними будь-які події 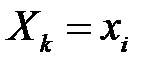
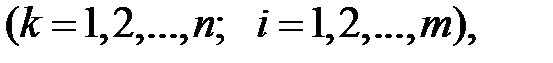 а значить, залежні випадкові величини
а значить, залежні випадкові величини 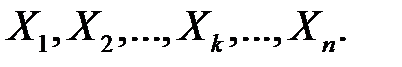
Однак, і для безповторної вибірки вибіркове середнє є «доброю» оцінкою. Про це свідчить теорема.
Теорема 2.4 Вибіркове середнє 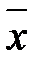 безповторної вибірки є незміщена і спроможна оцінка генерального середнього
безповторної вибірки є незміщена і спроможна оцінка генерального середнього 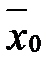 , причому
, причому
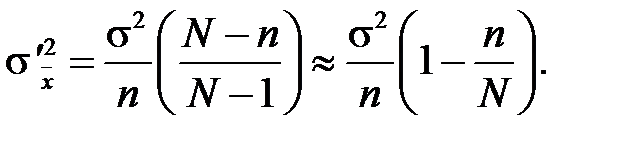 (2.12)
(2.12)
Теорему приймаємо без доведення.






