Рассмотрим общий порядок расчета переходных процессов классическим методом. Известными величинами считаются ЭДС или напряжения источников и номиналы входящих в схему сопротивлений, индуктивностей, емкостей; неизвестными – токи и напряжения.
Для независимых переменных составляются дифференциальные уравнения по законам Кирхгофа.
Независимыми переменными являются величины, которые не могут изменяться скачком: ток индуктивности и напряжение на емкости.
Если нам необходимо найти ток в некоторой к -й ветви, то исключим последовательно все остальные токи, останется одно уравнение для к -го тока и его производных:
В общем виде это уравнение можно записать
Правая часть fk (t) содержит в себе источники энергии.
Решение этого дифференциального уравнения ищем в виде суммы частного и общего решений.
Частное решение представляет собой значение тока в послекоммутационном установившемся режиме. Этот ток зависит только от источников fk (t) и называется принужденной составляющей. Для определения принужденной составляющей применяются любые методы расчета электрических цепей в послекоммутационном установившемся режиме.
Общее решение по физической сути определяет электромагнитные процессы, происходящие в электрической цепи при отсутствии источников энергии. Если в цепи в момент коммутации имелись запасы электромагнитной энергии, то в отсутствие источников эта энергия не будет пополняться, но будет рассеиваться на резистивных элементах. Поэтому токи и напряжения в конечном итоге при t = ∞ будут стремиться к нулю. Эти составляющие по своему характеру не зависят от внешних источников и называются свободными составляющими.
Свободная составляющая к -го тока определяется решением дифференциального уравнения этого тока при нулевых источниках:
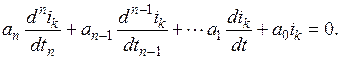
Для решения этого уравнения составляем характеристическое уравнение, заменяя символ дифференцирования параметром р:
, следовательно, 
и так далее.
Характеристическое уравнение будет иметь следующий вид:
Решая это уравнение, находим корни характеристического уравнения р 1, р 2,…, рп.
Решение для свободной составляющей тока ищем в виде
.
Здесь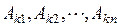 
– постоянные интегрирования, которые определяются с использованием законов коммутации и независимых начальных условий.
Независимыми начальными условиями называют значения независимых переменных в первый момент после коммутации t = 0.
Переходные процессы при включении индуктивной
