Любую симметричную Т- или П-схему четырехполюсника можно представить в виде комбинации Г-схем.
Если цепочка собрана из Т-звеньев, то она должна начинаться и кончаться продольным сопротивлением Z 1/2, если из П-звеньев, то она должна начинаться и кончаться поперечным сопротивлением 2 Z 1.
В упрощенном виде схему Т- или П-фильтра можно представить в виде рис. 10.1 а или б, соответственно.
Пусть электрический фильтр представляет собой комбинацию Т-схем.
Вспомним, что для Т-схемы коэффициент А связан с сопротивлениями эквивалентной схемы соотношением
.
Для коэффициента передачи справедливо соотношение 
.
Для симметричного четырехполюсника A=D и 
.
Исходя из приведенной схемы замещения, получим
.
В зоне прозрачности α = 0, следовательно, 
.
Учитывая, что гиперболический косинус мнимого аргумента равен тригонометрическому косинусу модуля этого аргумента, получим
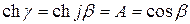(10.1)
Так как 
, то 
, следовательно,
, или 
, или 
.
Последнее выражение является условием пропускания реактивного фильтра. Из него следует, что продольное и поперечное сопротивления фильтра должны иметь различный характер: если Z 1 – индуктивность, то Z 2 – емкость и наоборот.
Предельные частоты, удовлетворяющие условиям пропускания, называются частотами среза. Таким образом, частоты среза удовлетворяют условиям:
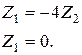
Эти условия можно интерпретировать при помощи частотных характеристик (рис. 10.2)
Из уравнения (10.1) следует:
.
 |
Мы выяснили, что отношение
- отрицательно, следовательно, для соs β будут справедливы соотношения:
или 
.
Используя формулы тригонометрических преобразований, получим:
→ 
.
Отсюда следует, что коэффициент фазы в полосе пропускания определится выражением
.
Исходя из граничных условий 
получим, что на границах полосы пропускания коэффициент фазы может принимать следующие значения: 
и 
.
Коэффициент затухания α в полосе пропускания равен нулю.
Фильтры нижних частот
Фильтры нижних частот состоят из продольных индуктивных сопротивлений и поперечных емкостных (рис. 10.3).
Здесь продольное сопротивление имеет индуктивный характер 
, поперечное – емкостный 
.
Определим тип фильтра. Найдем произведение продольного и поперечного сопротивлений
.
Из формулы видно, что это произведение не зависит от частоты, следовательно, фильтр типа k.
 |
Рассмотрим принцип действия фильтра. В этой схеме индуктивность обладает малым сопротивлением для низкочастотных сигналов, сопротивление емкости велико, поэтому низкочастотные сигналы будут проходить к потребителю, лишь незначительно ответвляясь через емкость С. С ростом частоты индуктивное сопротивление возрастает и сигналы высоких частот уже не будут проходить к потребителю, а будут замыкаться через емкость, которая обладает малым сопротивлением для высокочастотных сигналов.
Определим полосу прозрачности фильтра из условия пропускания:
Обозначим частоту среза 
. Тогда получим
или 
.
Таким образом, идеальный (не содержащий активного сопротивления) фильтр пропускает частоты от нуля до частоты среза.
В полосе прозрачности
.
В зоне затухания
.
 |
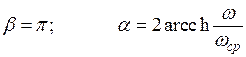На рис. 10.4 показаны частотные зависимости коэффициента затухания и коэффициента фазы низкочастотного фильтра.
Фильтры верхних частот
 |
Фильтр верхних частот состоит из продольных емкостных сопротивлений и поперечных индуктивных (рис. 10.5).
Емкостные сопротивления малы для высокочастотных сигналов и велики для низкочастотных, поэтому сигналы высоких частот проходят на нагрузку, а низкочастотные замыкаются через индуктивность.
Как видно из приведенной схемы, продольное сопротивление 
, а поперечное 
. Произведение продольного и поперечного сопротивлений
не зависит от частоты, следовательно, фильтр типа k.
Полоса прозрачности фильтра определится из условия:
, или 
В данном случае частота среза определяется выражением
.
Полоса пропускания будет лежать в пределах от частоты среза до бесконечности 
.
В полосе прозрачности 
.
В зоне затухания 
.
 |
Частотные зависимости коэффициента затухания и коэффициента фазы низкочастотного фильтра показаны на рис. 10.6.
Полосовой фильтр
Полосовым называется фильтр, полоса пропускания которого ограничена зонами затухания как со стороны низких, так и со стороны высоких частот.
Полосовые фильтры представляют собой соединение фильтров верхних и нижних частот. При этом продольное сопротивление Z 1 состоит из последовательно соединенных индуктивности и емкости, а поперечное сопротивление Z 2 представляет собой параллельное соединение индуктивности и емкости (рис. 10.7).
 |
Параметры последовательных и параллельных контуров подбираются такими, чтобы они были настроены на одну и ту же резонансную частоту, которая определяется выражением
.
На резонансной частоте сопротивление последовательного контура равно нулю, для параллельного контура нулю равна проводимость, следовательно, сопротивление бесконечно велико. Поэтому сигналы частот близких к резонансной будут пропускаться контуром. При отклонении частоты от резонансной в сторону низких или высоких частот сопротивление последовательного контура будет возрастать, а сопротивление параллельного контура уменьшаться, что приведет к ослаблению сигнала, поступающего на нагрузку.
Определим тип фильтра.
;
.
Отсюда
.
Поскольку произведение продольного и поперечного сопротивлений не зависит от частоты, то фильтр типа k.
Граничные частоты или частоты среза находятся из соотношения
, или 
.
Решая это уравнение, получим:
.
Полоса прозрачности фильтра ограничена частотами среза
,
то есть зависит только от индуктивности последовательного контура и емкости параллельного.
В полосе прозрачности
В полосе затухания
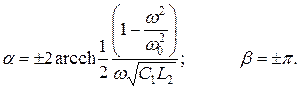
Частотные характеристики коэффициентов затухания и фазы представлены на рис. 10.8.
 |
Чем уже полоса пропускания, тем большее затухание в полосе затухания.
Заградительный фильтр
Заградительный фильтр имеет зону зтухания, ограниченную со стороны нижних и верхних частот зонами прозрачности. Такой фильтр состоит из продольных сопротивлений, представляющих собой параллельное соединение индуктивности и емкости, и поперечных, являющихся последовательным соединением индуктивности и емкости (рис. 10.9).
 |
Параметры схемы подбираются таким образом, чтобы последовательный и параллельный колебательные контуры были настроены на одну и ту же резонансную частоту.
Резонансная частота определяется выражением
.
На резонансной частоте параллельный контур обладает бесконечно большим сопротивлением, тогда как сопротивление последовательного контура равно нулю, следовательно, сигналы частот, близких к резонансной, не будут пропускаться фильтром. При отклонении частоты от резонансной в сторону низких или высоких частот сопротивление параллельного контура будет уменьшаться, а последовательного увеличиваться, что приведет к усилению сигнала, поступающего на нагрузку.
Продольное и поперечное сопротивления, соответственно, равны:
; 
.
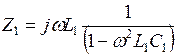Тогда произведение продольного и поперечного сопротивлений
.
Поскольку произведение продольного и поперечного сопротивлений не зависит от частоты, то фильтр типа k.
Граничные частоты или частоты среза находятся из соотношения
, или 
.
Решение этого уравнения дает
.
Заградительный фильтр прозрачен для частот от нуля до частоты среза ω 1 и от частоты среза ω 2 до бесконечности. Между частотами ω 1 и ω 2 лежит полоса затухания, ширина которой определяется из соотношения
.
В полосе прозрачности
В полосе затухания
 |
Частотные характеристики коэффициентов затухания и фазы представлены на рис. 10.10.
Реальные характеристики всех фильтров несколько отличаются от идеальных. В полосе прозрачности 
, поскольку невозможно добиться полного согласования нагрузочного и характеристического сопротивлений.
Контрольные вопросы и задания
1. Дайте определение электрического фильтра.
2. Приведите классификацию электрических фильтров.
3. Что называют полосой пропускания и зоной затухания фильтра?
4. Какими условиями определяется область пропускания реактивных электрических фильтров?
5. Приведите электрическую схему и объясните принцип действия фильтра нижних частот.
6. Какой вид имеют частотные характеристики коэффициента затухания и коэффициента фазы для фильтра нижних частот?
7. Приведите электрическую схему и объясните принцип действия фильтра верхних частот.
8. Какой вид имеют частотные характеристики коэффициента затухания и коэффициента фазы для фильтра верхних частот?
9. Какой фильтр называется полосовым?
10. Приведите схему и объясните принцип действия полосового фильтра.
11. Какой вид имеют частотные характеристики коэффициента затухания и коэффициента фазы для полосового фильтра?
12. Какой фильтр называется заградительным?
13. Приведите схему и объясните принцип действия заградительного фильтра.
14. Какой вид имеют частотные характеристики коэффициента затухания и коэффициента фазы для заградительного фильтра?
