Рассмотрим работу тепловой машины. Пусть Q1 – теплота, полученная рабочим телом (идеальным газом) в нагревателе; Q2 – теплота, отданная рабочим телом в холодильнике; Т1 – Т2 – абсолютные температуры нагревателя и холодильника соответственно. Работа (А) совершается машиной за счет разности теплот Q1 и Q2: А = Q1 – Q2. Термодинамический коэффициент полезного действия (η) тепловой машины определяется температурами нагревателя и холодильника:
η = 
(1.43)
Преобразуем уравнение (1.43)
1 - 
; 
; 
т.е. Σ 
(1.44)
где 
- приведенная теплота, имеющая размерность теплоемкости (Дж/К).
В идеальной тепловой машине расширение и сжатие рабочего тела происходит по двум изотермам и двум адиабатам, образующим в координатах v-p так называемый цикл Карно.
 |
Рис. 1.9 Основной термодинамический цикл. (цикл Карно)
Как известно из курса технической термодинамики, цикл состоит из четырех процессов:
1. Изотермического расширения за счет теплоты Q1, подведенной к газу при температуре Т1;
2. Адиабатического расширения;
3. Изотермического сжатия при температуре Т2; в этом процессе газ теряет Q2 единиц теплоты;
4. Адиабатического сжатия до исходного состояния.
Если при этом процессы расширения и сжатия проводить, изменяя давление на бесконечно малую величину dv, тоже будет бесконечно малым, т.е. в любой момент процесс может быть направлен в противоположную сторону, соответствующим элементарным изменениям параметров. Расширение и сжатие идеального газа происходит строго по изотермам и адиабатам, точнее, с бесконечно малыми отступлениями от них.
Описанный цикл Карно является равновесным (обратимым).
Выражение (1.44) означает, что алгебраическая сумма приведенных теплот по равновесному (обратимому) циклу Карно равна нулю.
Применив (1.44) к бесконечно малому (элементарному) циклу Карно, получим
или 
Любой обратимый цикл можно заменить бесконечно большим числом n элементарных циклов Карно, следовательно, можно записать:
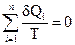
В пределе, n → ∞, получим
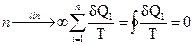(1.45)
Из высшей математике известно, что если интеграл по замкнутому контуру равен нулю, то подинтегральное выражение является полным дифференциалом некоторой функции. Эту функцию Клаузиус назвал энтропией (S). Для элементарного обратимого процесса
dS = 
(1.46)
или ∆S = S2 – S1 = 
, где 1 и 2 – начальное и конечное состояние системы.
Следовательно, энтропия есть функция состояния, изменение которой равно алгебраической сумме приведенных теплот по всем элементам равновесного процесса.
По первому закону термодинамики, если δА' = 0, δQ = dU + pd v. Поскольку работа, совершаемая системой в необратимом процессе, всегда меньше работы, производимой в квазистатическом (обратимом) процессе (Анеобр < Аобр), то
dS > 
(1.47)
объединяя (1.46) и (1.47), получим
dS ≥ 
или Т*dS ≥ δQ (1.48)
Неравенство (1.48) является математическим выражением второго закона термодинамики, где знак равенства относится к обратимым процессам, а знак неравенства к необратимым.
Энтропия, как и приведенная теплота имеет размерность [S] = Дж/К, или в применении к одному молю вещества [S] = Дж/мольК. Если рассматривать систему изолированную от окружающей среды, в которой δQ = 0, то при применении уравнения (1.48) к этой системе, получим
dS ≥ 0 (1.49)
Следовательно, в изолированной системе для обратимого процесса dS = 0, S = const, а для необратимого (самопроизвольного) процесса dS > 0.
Таким образом, в изолированной системе самопроизвольно могут протекать процессы, сопровождающиеся увеличением энтропии. Следовательно, энтропия в изолированной системе является критерием направленности самопроизвольного процесса.
Только возрастанием энтропии можно объяснить самопроизвольное протекание в изолированных системах таких процессов, как передача теплоты от более нагретого тела к менее нагретому или взаимная диффузия двух или нескольких химических не взаимодействующих газов.
Для удобства запоминания все сказанное об энтропии изобразим схемой.
| Не изолированные (открытые, закрытые системы) | |
| Обратимые процессы
dS =
| Необратимые процессы
dS >
|
| Изолированные системы | |
| dS = 0 S = const | dS > 0 S - растет |
С помощью понятия энтропии можно объединить оба начала термодинамики. Подставив в уравнение (1.48) значение δQ из первого закона термодинамики, получим неравенство:
Т*dS ≥ dU + РdV + δA` (1.50)
Представляющие собой обобщенное выражение первого и второго законов термодинамики.
Решим уравнение относительно δA`
δA` ≤ Т*dS – dU – РdV(1.51)
в такой форме обобщенное уравнение двух начал показывает, что полезная работа максимальна только тогда, когда процесс протекает термодинамически обратимо. Если работа производится системой только против внешнего давления (δA` = 0), то уравнение (1.50) примет вид:
Т*dS ≥ dU + рdV(1.52)
из уравнения видно, что энтропия является функцией внутренней энергии и объема S=f(U, V).
