Уравнение (1.12) можно переписать в виде
- ΔU = - Q + А (1.13)
Т.е. убыль внутренней энергии системы расходуется на выделение теплоты и совершение работы.
Знак Δ (дельта, греч.) – означает конечную разность свойства системы. Для бесконечно малого изменения состояния уравнений 1.12 примет вид
δQ = dU + δA = dU + РdV + δA` (1.14)
где δА – сумма всех элементарных работ,
δA` - работа против гравитационных, электрических, магнитных и прочих сил, т.е. не связанная с изменением термодинамических параметров (так называемая полезная работа);
РdV – работа преодоления внешнего давления Р, необходимое для удержания системы в состоянии механического равновесия. Если на систему действует только постоянное внешнее давление, а другие силы отсутствуют, то A' = 0 и уравнение (1.14) принимает вид:
δQ = dU + РdV(1.15)
В этом уравнении Р можно считать давлением в системе только для равновесных (обратимых) процессов.
Процессы в которых участвуют системы могут протекать при различных условиях:
1. Изохорный процесс.
При изохорном процессе V= const, РdV= 0, согласно уравнению (1.15)
δQ V = dU (1.16)
и для конечного изменения
Q V =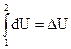 
(1.17)
Таким образом, в изохорном процессе величина δQ V приобретает свойства полного дифференциала и теплота не зависит от пути превращения. Если теплоту измерять в калориметре с постоянным объемом, то можно определять приращение (или убыль) внутренней энергии системы. Реакции при V = const, могут быть осуществлены: а) в закрытой бомбе; б) между твердыми телами и жидкостями без выделения газа; в) между газами, если число молекул остается постоянным, например, H2 + Cl2 = 2HCl (газ)
2. Для изобарного процесса (р = const), в котором совершается только работа расширения уравнения (1.15), можно записать
δQр = dU + рd V = d (U + P V) = dН (1.18)
Сумма внутренней энергии и произведения объема вещества на внешнее давление называют энтальпией и обозначают буквой Н. Произведение р V численно равно работе, которую надо совершить, что бы данную систему ввести в пространство объемом V с давлением р. Следовательно, оно представляет собой ту потенциальную энергию системы, которая обусловлена давлением р в объеме V. Поэтому произведение р V – называют потенциальной энергией давления.
Последняя, не имеет ничего общего с потенциальной энергией положения системы во внешнем силовом поле.
Термодинамическая система, в которой учитывается внутренняя энергия и потенциальная энергия давления, называется расширенной системой.
Интегрирование уравнения и простое преобразование дают:
Qр = ΔU + PΔ V = U2 – U1 + р (V 2 – V 1) = (U2 + р V 2) – (U1 + р V 1) = Н2 – Н1 = ΔН (1.19)
Следовательно, теплота, поглощенная в изобарном процессе, служит мерой приращения энтальпии системы. Так же, как и внутренняя энергия, энтальпия системы является функцией состояния.
3. Изотермический процесс
Передача теплоты при Т = const от одного тела к другому является квазистатическим процессом. Для идеального газа, а так же для реального при невысоких давлениях внутренняя энергия является функцией температуры. Поэтому при изотермических процессах U = const и уравнение (1.15) принимает вид:
δQ = рd V (1.20)
или
Q = А (1.21)
Следовательно, при изотермическом процессе сообщенная системе теплота целиком превращается в работу расширения.
4. Адиабатический процесс
При адиабатическом процессе δQ = 0 и уравнение (1.15) принимает вид:
δА = - dU (1.22)
или
А = - ΔU (1.23)
Таким образом, при адиабатическом процессе работа расширения совершается системой за счет убыли ее внутренней энергии.
Теплоемкость
Теплоемкостью называется отношение количества теплоты Q, поглощенной i-тым компонентом системы с массой m или количеством v к повышению температуры от Т1 до Т2. Взаимосвязь между Q, массой i-го компонента (или количеством вещества) и изменением температуры можно представить уравнением
Q = 
v 
(1.24)
Где, 
- средняя удельная теплоемкость;
- Средняя молярная теплоемкость.
При физико-химических процессах обычно используется молярная теплоемкость.
При v = 1 Q = 
(1.25)
= 
(1.26)
Где, – средняя молярная теплоемкость i-го компонента системы (индекс m – можно опустить).
Если сообщить системе, содержащей 1 моль вещества, бесконечно малое количество теплоты δQ, то температура ее повысится на бесконечно малую величину dТ.
Тогда,
δQ = CdT (1.27)
С = δQ / dT (1.28)
Где С - истинная молярная теплоемкость. Согласно уравнениям (1.26) и (1.28) молярная теплоемкость численно равна количеству теплоты, которое необходимо сообщить 1 моль вещества для нагревания на 1 К. Размерности молярной теплоемкости- (Дж/ моль∙К)
В соответствии с определением теплоемкости и первым законом термодинамики для изохорного и изобарного процессов нагревания i-го вещества
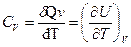(1.29)
(1.30)
Где, С v и Ср теплоемкости при постоянном объеме и давлении соответственно. Так как для одного моля идеального газа
Н = U + pv = U + RT, то СР - Сv = R (1.31)
Смысл этого выражения заключается в том, что при нагревании одного моля идеального газа на 10 при Р = const сообщаемое газу тепло расходуется не только на изменение внутренней энергии газа, но и на совершение работы против внешнего давления, равного давлению газа; при нагревании же газа при V = const тепло расходуется только на изменение его внутренней энергии.
Для реальных газов СР - Сv > R, чем выше давление газа, тем больше будет разность теплоемкостей отличаться от R.
Для жидкостей эти теплоемкости практически одинаковы. Это указывает на то, что теплоемкость жидкостей практически не зависит от давления. Для твердых веществ, обладающих небольшим коэффициентом теплового расширения, можно так же принять СР = Сv.
Если экспериментальные данные для теплоемкостей веществ твердом или жидком состояниях отсутствуют то, для их оценки прибегают к ряду приближенных эмпирических правил. Одним из таких является правило Дюлонга и Пти (1819 г.): атомная теплоемкость при постоянном объеме для любого твердого простого вещества приблизительно равна 25 Дж/моль∙К. Это правило более или менее оправдывается для элементов, атомная масса которых выше, чем у калия, и при относительно высоких температурах, близких к температурам плавления твердых веществ.
Если допустить неизменность теплоемкостей элементов при образовании химического соединения, то теплоемкость последнего будет равна 25 * n Дж/ моль∙К, где n – число атомов, входящих в молекулу. Это эмпирическое правило, которое так же является приближенным, впервые было предложено Нейманом (1831 г.) и в дальнейшем развито Коппом.
При вычислении теплоемкости сложного вещества по правилу Неймана-Коппа (правило аддитивности) более близких результатов к опытным данным для теплоемкости можно ожидать, если принять для легких элементов следующие значения атомных теплоемкостей:
| С | Н | В | Si | О | F | Р | S | Дж/моль∙К |
| 7,53 | 9,62 | 11,3, | 15,90 | 16,74 | 20,92 | 22,59 | 22,59 |
а для остальных элементов 25,94 Дж/моль∙К.
Пример 1: На основании правила Неймана-Коппа вычислить теплоемкость оксида бора (B2O3).
Решение: Исходя из данных для атомных теплоемкостей бора и кислорода, получим, Ср(B2O3) = 2 * 11,30 + 3 * 16,74 = 72,82 Дж/моль∙К
Экспериментальное значение Ср(B2O3) = 62,97 Дж/моль∙К при температуре 250С. Расхождение 15,6 %. Исходя из правила аддитивности, теплоемкость сплава, состоящего из двух веществ, может быть вычислена приближенно по соотношению
Ср = х1 * Ср1 + х2 * Ср2 (1.32)
Где Ср1, Ср2 – теплоемкости чистых веществ;
х1, х2 – содержание веществ в сплаве (мольные доли).
Правило аддитивности лежит и в основе уравнения Ср = 32,43 n, (1,33), где n – число атомов, входящих в молекулу неорганического вещества, и которое было предложено Келли для вычисления теплоемкости высококипящих чистых неорганических жидкостей (ВеО, BeCl2, MgBr2).
Предложено так же значительное число эмпирических методов позволяющих приближенно рассчитать молярные теплоемкости органических жидкостей.
Например, можно применить метод, в котором используются атомно-групповые составляющие теплоемкостей, полученные при анализе экспериментальных данных о теплоемкостях большого числа соединений.
Таблица 1.
