Гіпотеза про рівність декількох дисперсій нормально розподілених ознак генеральної сукупності за вибірками однакового об'єму

Нехай ознаки генеральної сукупності розподілені нормально. З цієї сукупності взято l незалежних вибірок однакового об'єму n і для кожної з них знайдені виправлені вибіркові дисперсії , всі з однаковим числом ступенів свободи k = n -1. Потрібно для рівня значущості перевірити гіпотезу про однорідність дисперсій;

. (4.30)

Розглянемо випадкову величину

, (4.31)

де - найбільша із всіх виправлена вибіркова дисперсія. Розподіл цієї випадкової величини залежить тільки від числа ступенів свободи k = n -1 і кількості вибірок l.

Для заданого рівня значущості критична область , де = (, k, l) знаходять з таблиці критичних точок розподілу Кочрена (таблиця 7 у додатку). Критерій узгодження формулюється:

Нехай – точкова оцінка випадкової величини , обчислена на основі l незалежних вибірок однакового об'єму. Тоді:

1. Якщо > , то гіпотеза H ₀ – відхиляється.

2. Якщо < , то гіпотеза H ₀ – приймається.

Приклад 4.16. Трьома експертами за 100-бальною шкалою проведена оцінка вагомості всіх факторів, що впливають на внутрішньогосподарський ризик, і отримані наступні результати:

ІІ

ІІІ

Чи можна для рівня значущості стверджувати про узгодженість оцінок експертів (припускається, що оцінки експертів розподілені нормально).

Розв’язок. Вибіркове середнє для оцінок кожного експерта . Обчислимо виправлені вибіркові дисперсії . Для цього спочатку оцінки кожного експерта представимо у вигляді наступних статистичних рядів:

x_i

k_i

x_i

k_i

Тоді:

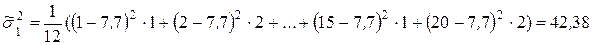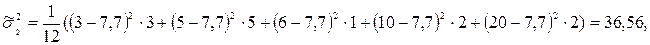
Оскільки 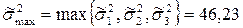, то точкова оцінка випадкової величини (4.31) рівна:

За таблицею 7 у додатку для , , , . Враховуючи, що , то можемо стверджувати, що оцінки експертів узгоджені між собою.

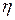4.5.6. Гіпотеза про рівність математичних сподівань двох нормально розподілених ознак і генеральної сукупності з невідомими дисперсіями (залежні вибірки)

Нехай в генеральній сукупності досліджуються дві нормально розподілені випадкові величини (ознаки) і 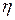, причому їх дисперсії невідомі. З цією метою взяті дві залежні вибірки однакового об’єму n, варіанти яких відповідно рівні x_i та y_i. Потрібно для рівня значущості перевірити нульову гіпотезу Н ₀: при альтернативній гіпотезі Н ₁: .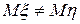

Позначимо , , . Випадкова величина має t -розподіл Стьюдента з ступенями свободи.

Критична область , де знаходять з таблиці 4 у додатку.

Нехай – точкова оцінка випадкової величини , обчислена на основі вибірки. Тоді, якщо , гіпотеза відхиляється, а в протилежному випадку – приймається.

Приклад 4.17. Для аналізу результатів вступних випробувань з мови (х_і) і математики (у_і) взята вибірка об’ємом і отриманий наступний емпіричний розподіл:

Для рівня значущості перевірити чи значимо відрізняються результати вступних випробувань з мови і математики між собою, при умові, що вони розподілені нормально.

Розв’язок. Знайдемо спочатку різниці

а потім вибіркове середнє . Враховуючи, що , обчислюємо:

Далі . За таблицею 4 додатку знаходимо t (0,05,40)=2,023. Оскільки 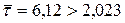, нульова гіпотеза відхиляється, тобто результати з мови і літератури значно відрізняються між собою.

4.5.7. Гіпотеза про рівність невідомої ймовірності р гіпотетичній ймовірності

Нехай для досить великого числа n незалежних випробувань, в кожному з яких ймовірність р появи подій стала, але невідома, знайдена відносна частина

. Потрібно для заданого рівняння значущості перевірити нульову гіпотезу .

Випадкова величина при справедливості нульової гіпотези має нормальний розподіл з параметрами (0,1).

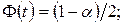При альтернативних гіпотезах , де - розв’язок рівняння при В останніх двох випадках - розв’язок рівняння .

Приклад 4.18. При аналізі результатів семестрового екзамену з деякого предмету отримано, що зі 110 студентів першого курсу 16 одержали негативну оцінку. Для рівня значущості перевірити нульову гіпотезу про те, що 10% студентів отримають негативну оцінку при альтернативній гіпотезі .

Розв’язок. Для випадкової величини шукаємо її точкову оцінку

За таблицею 2 додатку отримуємо, що , . Таким чином наше при пущення виявилось вірним.