Нехай 
– вибірка з неперервно розподіленої генеральної сукупності з функцією розподілу 
, а 
– вибірка з неперервно розподіленої генеральної сукупності з функцією розподілу 
. Потрібно перевірити нульову гіпотезу 
про співпадання розподілів обох вибірок. Для її перевірки М.В.Смірнов запропонував статистику
де 
і 
- емпіричні функції розподілу обох вибірок.
Розподіл статистики 
не залежить від гіпотетичних розподілів і 
, а при досить великих 
і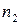 
випадкова величина 
має розподіл А.М.Колмогорова. Критична область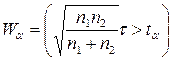 
, де 
знаходимо з таблиці 6 у додатку.
Приклад. 4.11. При експертній оцінці вагомості факторів „Операції з дочірними підприємствами” та „Форма розрахунків на підприємстві”, які впливають на внутрішньогосподарський ризик, групою з 20 експертів отримано наступні результати:
Для рівня значущості 
перевірити нульову гіпотезу 
про співпадання розподілів оцінок обох факторів.
Розв’язок. Обчислення проведемо, використовуючи таблицю 4.4.
Таблиця 4.4.
| хі | yi | 
| 
| 
|
| 0,05 0,05 0,25 0,45 0,5 0,9 0,9 0,9 0,95 | 0,05 0,1 0,15 0,35 0,55 0,9 0,95 | 0,05 0,1 0,1 0,05 0,05 0,1 0,05 |
Максимальне значення відхилення дорівнює 0,1. Тоді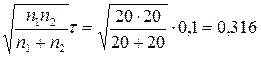 
. З таблиці 6 у додатку знаходимо 
як розв’язок рівняння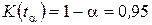 
. Оскільки 0,316<1,36, то гіпотеза приймається.
Критерій Колмогорова
Якщо обмежимося випадком, коли випадкова величина (ознака) x в генеральній сукупності є неперервною, то задачу про перевірку гіпотези H 0 ((4.5) або (4.10)) про розподіл для неї можна розв’язати і з допомогою іншого критерію узгодження, а саме, критерію Колмогорова.
Ідея його побудови полягає в наступному.
За міру відхилення теоретичних даних від емпіричних вибирають запропоновану А.М. Колмогоровим випадкову величину t у вигляді
, (4.16)
де 
– емпірична функція розподілу, а 
– теоретична функція розподілу, яка задається гіпотезою.
І, що найважливіше, розподіл випадкової величини (4.16) відомий і визначається наступною теоремою, яку ми також наводимо без доведення.
Теорема 4.2. При 
розподіл випадкової величини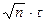 
незалежно від виду розподілу випадкової величини x прямує до розподілу Колмогорова:
, (4.17)
де 
- функція Колмогорова, яка протабульована у таблиці 6 у додатку.
Виходячи зі змісту даної теореми, рівняння для визначення критичної області W a=(
) для заданого рівня значущості a, згідно з рівнянням (4.2), запишеться у виді:
P(
)= a (4.18)
або
K(t a)=1- a. (4.19)
Розв’язуючи рівняння (4.19) для заданого a, за таблицею 6 отримаємо розв’язок ta. Це дозволяє сформулювати критерій узгодження Колмогорова таким чином: нехай 
– точкова оцінка випадкової величини t, яка отримується на основі вибірки (x 1, x 2,..., xn) з умови (4.16).
Тоді:
1. Якщо 
, то гіпотеза H 0 відхиляється;
2. Якщо ж 
, то гіпотеза H 0 приймається.
Приклад 4.12. Нехай результати вимірювань 1000 одиниць товару представляються у вигляді такої згрупованої вибірки:
| xi | 98,5 | 99,5 | 100,5 | 101,5 |
| |||||||
| ki |
Необхідно, користуючись критерієм Колмогорова, перевірити, чи узгоджуються отримані спостереження з гіпотезою про те, що похибка вимірювань x має нормальний закон розподілу з параметрами a =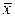 
=100,25 i s =1, якщо рівень значущості a =0,05.
Розв’язок. Оскільки, згідно з гіпотезою H 0, випадкова величина x є нормально розподіленою з параметрами a = 
=100,25 і s =1, то гіпотезу можна записати, як:
H 0: F x(x)=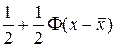 
,
де F (x) - відома функція Лапласа.
За таблицею 2 у додатку для функції Лапласа і на основі методики обчислення емпіричних функцій розподілу для заданої вибірки (4.20) побудуємо для зручності наступну таблицю:
| xi | F x(xi) | F *x(xi) | | F x(xi)- F *x(xi)| |
| 98,5 99,5 100,5 | 0,012 0,04 0,105 0,226 0,401 0,598 0,773 | 0,01 0,004 0,41 0,234 0,403 0,594 0,776 | 0,002 0,004 0,006 0,008 0,002 0,004 0,007 |
| 101,5 | 0,894 | 0,885 | 0,009 |
| 102,5 | 0,959 0,987 | 0,954 0,987 | 0,005 0,000 |
з якої випливає, що максимальне значення різниця | F x(xi)- F *x(xi)| приймає при xi =101,5 і дорівнює 0,009. Отже, точкова оцінка 
, а 
За таблицею 6 для функції Колмогорова для заданого рівня значущості a =0,05 отримаємо t 0,05=1,38.
Таким чином, 
, а, отже, згідно з критерієм Колмогорова, який сформульований вище, робимо висновок, що дану гіпотезу можна прийняти.
Розглянемо тепер приклади параметричних гіпотез.
ПАРАМЕТРИЧНІ ГІПОТЕЗИ
