(4.29)
яка при справедливості основної гіпотези не залежить від невідомих параметрів нормального розподілу. Крім того, 
і 
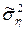не залежать від середніх значень вибірки, а / 
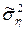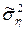і / мають χ 2 – розподіл з n 1-1 i n 2-1 cтупенями свободи і не залежать ні від середнього, ні від дисперсій, якщо справедлива основна гіпотеза (4.28). Оскільки / і / не залежать ні від середніх, ні від дисперсій, то їх відношення / 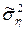також не залежить від середніх двох вибірок, як і від дисперсій двох вибірок, лише б дисперсії були рівні.
Тоді випадкова величина 
має розподіл Фішера з 
і 
ступенями свободи.
При альтернативних гіпотезах:
Н 1: 
;
Н 1: 
; Н 1: 
,
де 
знаходять з таблиці 8 додатку.
Нехай 
– точкова оцінка випадкової величини 
, обчислена на основі вибірки за формулою 4.29. Тоді, якщо 
, то гіпотеза відхиляється, а в протилежному випадку – приймається.
б) 
i 
– відомі.
В даному випадку гіпотеза перевіряється аналогічно до попередньої, але
де , – відомі середні генеральних сукупностей. Якщо вірна гіпотеза
H 0: 
то 
/ 
і 
/ розподілені за законом χ 2 відповідно з n 1 i n 2 ступенями свободи. Тому випадкова величина 
/ 
розподілена за законом Фішера з n 1 i n 2 ступенями свободи.
4.5.3. Гіпотеза про рівність математичного сподівання 
нормально розподіленої ознаки 
генеральної сукупності гіпотетичному значенню 
Нехай в генеральній сукупності досліджується нормально розподілена випадкова величина (ознака) з параметрами 
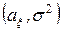. Проведено вибірку (
) об’єму n. Параметри та 
– невідомі. Відносно значення параметра висувається гіпотеза: Н 0: 
.
Оскільки значення математичного сподівання невідоме, то для перевірки гіпотези Н 0 використовується його точкова оцінка 
, яка у випадку нормально розподіленої випадкової величини 
має нормальний закон розподілу з параметрами 
. Тоді випадкова величина 
має t -розподіл Стьюдента з (n -1) ступенями свободи.
При альтернативних гіпотезах: Н 1: 
; Н 1: 
; Н 1: 
, де 
знаходять за таблицею 4 у додатку.
Нехай – точкова оцінка випадкової величини 
, обчислена на основі вибірки. Тоді, якщо 
, то гіпотеза відхиляється, а в протилежному випадку – приймається.
Приклад 4.14. За вибіркою об’єму 
, взятою з результатів вступних випробувань, знайдено вибіркову середню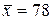 
і виправлену вибіркову дисперсію 
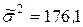. Допустивши, що результати випробувань розподілені нормально, для рівня значущості 
перевірити нульову гіпотезу Н 0: 
при Н 1: 
.
Розв’язок. За формулою знаходимо, що 
. З таблиці 4 у додатку отримаємо 
. Оскільки 
, то гіпотеза приймається.
Зауваження 4.10. Якщо дисперсія відома, то 
. При альтернативних гіпотезах: Н 1: 
, де 
– розв’язок рівняння 
; Н 1: 
; Н 1: 
. В останніх двох випадках – розв’язок рівняння 
.
4.5.4. Гіпотеза про рівність дисперсії 
нормально розподіленої ознаки генеральної сукупності гіпотетичному значенню 
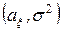Нехай в генеральній сукупності досліджується нормально розподілена випадкова величина (ознака) з параметрами . Проведено вибірку () об’єму n. Параметри та – невідомі. Відносно значення параметра висувається гіпотеза Н 0: 
.
Оскільки значення невідоме, то для перевірки гіпотези Н 0 використаємо його точкову оцінку 
. Тоді випадкова величина 
має розподіл 
з (n -1) ступенями свободи.
При альтернативних гіпотезах:
Н 1: 
;
Н 1: 
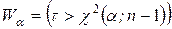; Н 1: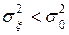 
, де 
, 
, 
, 
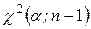знаходять за таблицею 5 у додатку.
Нехай – точкова оцінка випадкової величини , обчислена на основі вибірки. Тоді, якщо , то гіпотеза відхиляється, а в протилежному випадку – приймається.
Приклад 4.15. Робота групи експертів при оцінюванні вагомості впливу факторів на різні види ризику вважається узгодженою, якщо дисперсія результатів оцінювання не повинна перевищувати 
. З результатів оцінювання взяли вибірку об’ємом 
і отримали наступний емпіричний розподіл балів:
| xi |
| |||||||||
| ki |
де xi – бали, присвоєні кожним експертом, ki – кількість експертів, які присвоїли дані бали.
Допустивши, що результати оцінювання розподілені нормально, для рівня значущості 
перевірити нульову гіпотезу Н 0: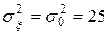 
, при альтернативній гіпотезі Н 1: 
.
Розв’язок. Обчислюємо і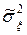 
:
,
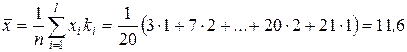За формулою знайдемо, що точкова оцінка 
. З таблиці 5 у додатку отримаємо 
.
Оскільки 
, то гіпотеза приймається. Тобто з надійністю 0,95 можна стверджувати, що результати оцінювання вагомості впливу фактору на елемент аудиторського ризику, виставлені кожним експертом, є узгоджені між собою.
