6. Тонкий длинный стержень равномерно заряжен с линейной плотностью заряда τ =10 мкКл/м. На продолжении оси стержня на расстоянии d =20 см от ближайшего его конца находится точечный заряд 
нКл. Определить силу взаимодействия заряженного стержня и точечного заряда.
7. Тонкий очень длинный стержень равномерно заряжен с линейной плотностью заряда τ =10 мкКл/м. На перпендикуляре к оси стержня, идущем из его конца, находится точечный заряд нКл. Расстояние от конца стержня до заряда d =20 см. Определить силу взаимодействия заряженного стержня и точечного заряда.
8. Тонкая длинная нить длиной l =20 см равномерно заряжена с линейной плотностью заряда τ =10 нКл/м. На расстоянии d =10 см от нити против ее середины находится точечный заряд 
нКл. Определить силу, действующую на этот заряд со стороны нити.
9. Тонкий длинный стержень равномерно заряжен с линейной плотностью заряда τ =10 мкКл/м. Какова сила, действующая на точечный заряд нКл, находящийся на расстоянии d =20 см от стержня вблизи его середины?
10. Тонкое кольцо радиусом 
см несет равномерно распределенный заряд 
мкКл. На перпендикуляре к плоскости кольца, восстановленном из его середины, находится точечный заряд нКл. Какова сила, действующая со стороны заряженного кольца на заряд 
,если он удален от центра на расстояние d1 =20 см, d2 =2 см?
11. Тонкий стержень длиной l =12 см заряжен с линейной плотностью τ =200 нКл/м. Найти напряженность электрического поля в точке, находящейся на расстоянии d =5 см от стержня, напротив его середины.
12. Тонкий стержень длиной l =12 см заряжен с линейной плотностью τ =400 нКл/м. Найти напряженность электрического поля в точке, расположенной на перпендикуляре к стержню, проведенному через один из его концов на расстоянии d =8 см.
13. Определить напряженность поля, создаваемого зарядом, равномерно распределенным по тонкому прямому стержню длиной l =40 см с линейной плотностью τ =200 нКл/м в точке, лежащей на продолжении оси стержня на расстоянии d =20 см от ближайшего конца.
14. Напряженность нормального электрического поля земной атмосферы в среднем равна Е =130 В/м и направлена вертикально вниз. Какое ускорение сообщает поле пылинке массой m =100 нг, несущей положительный заряд Q =16 аКл? [ а – атто=10-18].
15. Заряд Q =20 нКл равномерно распределен на металлической нити длиной l =1 м. Определить напряженность поля в точке, находящейся на расстоянии d =10 см от нити и равноудаленной от её концов.
16. По тонкому кольцу радиусом 
см равномерно распределен заряд с линейной плотностью τ =0,2 мкКл/м. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке, находящейся на расстоянии d =2 R от его центра.
17. По тонкому полукольцу радиусом равномерно распределен заряд Q =20 мкКл с линейной плотностью τ =0,1 мкКл/м. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке, совпадающей с центром кольца.
18. Четверть тонкого кольца радиусом см равномерно распределен заряд Q =0,05 мкКл. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке, совпадающей с центром кольца.
19. По тонкому кольцу равномерно распределен заряд Q =10 нКл с линейной плотностью τ =0,01 мкКл/м. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке, находящейся на расстоянии d = R от его центра.
20. Две трети тонкого кольца радиусом см равномерно распределен заряд с линейной плотностью τ =0,2 мкКл/м. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке, совпадающей с центром кольца.
21. На двух концентрических сферах радиусом R и 2 R равномерно распределены заряды с поверхностными плотностями σ1 и σ2. Требуется: 1) используя теорему Остроградского-Гаусса, найти зависимость 
напряженности электрического поля от расстояния для областей: I, II и III (рис. 43). Принять σ1 =4 σ, σ2 = σ; 2) вычислить напряженность поля в точке, удаленной от центра на расстояние r, и указать направление вектора напряженности. Принять σ =30 нКл/м2, r =1,5 R; 3) построить график .
 |
Рис. 43
22. На двух концентрических сферах радиусом R и 2 R равномерно распределены заряды с поверхностными плотностями σ1 и σ2. Требуется: 1) используя теорему Остроградского-Гаусса, найти зависимость напряженности электрического поля от расстояния для областей: I, II и III. Принять σ1 = σ, σ2 = -σ; 2) вычислить напряженность поля в точке, удаленной от центра на расстояние r, и указать направление вектора напряженности. Принять σ =0,1 мкКл/м2, r =3 R; 3) построить график .
23. На двух концентрических сферах радиусом R и 2 R равномерно распределены заряды с поверхностными плотностями σ1 и σ2. Требуется: 1) используя теорему Остроградского-Гаусса, найти зависимость напряженности электрического поля от расстояния для областей: I, II и III. Принять σ1 = - 4 σ, σ2 = σ; 2) вычислить напряженность поля в точке, удаленной от центра на расстояние r, и указать направление вектора напряженности. Принять σ =50 нКл/м2, r =1,5 R; 3) построить график .
24. На двух концентрических сферах радиусом R и 2 R равномерно распределены заряды с поверхностными плотностями σ1 и σ2. Требуется: 1) используя теорему Остроградского-Гаусса, найти зависимость напряженности электрического поля от расстояния для областей: I, II и III. Принять σ1 = - 2 σ, σ2 = σ; 2) вычислить напряженность поля в точке, удаленной от центра на расстояние r, и указать направление вектора напряженности. Принять σ =0,1 мкКл/м2, r =3 R; 3) построить график .
25. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями σ1 и σ2. Требуется: 1) используя теорему Остроградского-Гаусса и принцип суперпозиций полей, найти зависимость 
напряженности электрического поля от расстояния для областей: I, II и III (рис. 44). Принять σ1 = 2 σ, σ2 = σ; 2) вычислить напряженность поля в точке, расположенной слева от плоскостей, и указать направление вектора напряженности. Принять σ =0,1 мкКл/м2, r =3 R; 3) построить график .
 | |||
| |||
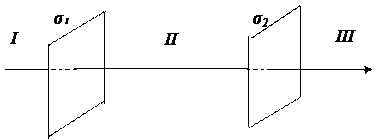Рис. 44
26. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями σ1 и σ2. Требуется: 1) используя теорему Остроградского-Гаусса и принцип суперпозиций полей, найти зависимость напряженности электрического поля от расстояния для областей: I, II и III. Принять σ1 = - 4 σ, σ2 =2 σ; 2) вычислить напряженность поля в точке, расположенной между плоскостями, и указать направление вектора напряженности. Принять σ =40 нКл/м2; 3) построить график .
27. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями σ1 и σ2. Требуется: 1) используя теорему Остроградского-Гаусса и принцип суперпозиций полей, найти зависимость напряженности электрического поля от расстояния для областей: I, II и III. Принять σ1 = σ, σ2 = - 2 σ; 2) вычислить напряженность поля в точке, расположенной справа от плоскостей, и указать направление вектора напряженности. Принять σ =20 нКл/м2; 3) построить график .
28. На двух коаксиальных бесконечных цилиндрах радиусами R и 2 R равномерно распределены заряды с поверхностными плотностями σ1 и σ2. Требуется: 1) используя теорему Остроградского-Гаусса, найти зависимость напряженности электрического поля от расстояния для областей: I, II и III (рис. 45). Принять σ1 = - 2 σ, σ2 = σ; 2) вычислить напряженность поля в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора напряженности. Принять σ =50 нКл/м2, r =1,5 R; 3) построить график .
 |
|
|
|
|
|
|
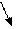
Рис. 45
29. На двух коаксиальных бесконечных цилиндрах радиусами R и 2 R равномерно распределены заряды с поверхностными плотностями σ1 и σ2. Требуется: 1) используя теорему Остроградского-Гаусса, найти зависимость напряженности электрического поля от расстояния для областей: I, II и III (рис. 45). Принять σ1 = σ, σ2 = - σ; 2) вычислить напряженность поля в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора напряженности. Принять σ =60 нКл/м2, r =3 R; 3) построить график .
30. На двух коаксиальных бесконечных цилиндрах радиусами R и 2 R равномерно распределены заряды с поверхностными плотностями σ1 и σ2. Требуется: 1) используя теорему Остроградского-Гаусса, найти зависимость напряженности электрического поля от расстояния для областей: I, II и III (рис. 45). Принять σ1 = - σ, σ2 =4 σ; 2) вычислить напряженность поля в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора напряженности. Принять σ =30 нКл/м2, r =4 R; 3) построить график .
31. Тонкий стержень согнут в кольцо радиусом R =10 см и равномерно заряжен с линейной плотностью τ =800 нКл/м. Определить потенциал в точке, расположенной на оси кольца на расстоянии d =10 см от его центра.
32. Тонкая квадратная рамка равномерно заряжена с линейной плотностью заряда τ =200 нКл/м. Определить потенциал поля в точке пересечения диагоналей.
33. Четыре одинаковых капли ртути, заряженных до потенциала φ =10 В, сливаются в одну. Каков потенциал образовавшейся капли?
34. Поле образовано точечным диполем с электрическим моментом р =200 пКл∙м. Определить разность потенциалов двух точек поля, расположенных симметрично относительно диполя на его оси на расстоянии d =40 см от центра диполя.
35. Электрическое поле образовано бесконечно длинной заряженной нитью, линейная плотность заряда которой τ =20 пКл/м. Определить разность потенциалов двух точек поля отстоящих от нити на расстоянии d1 =8 см и d2 =12 см.
36. Точечные заряды Q1 =1 мкКл и Q2 =0,1 мкКл находятся на расстоянии r =10 см друг от друга. Какую работу совершат силы поля, если второй заряд, отталкиваясь от первого, удалится от него на расстояние: 1) 10 м; 2) бесконечность.
37. Тонкий стержень согнут в полукольцо. Стержень заряжен с линейной плотностью τ =133 нКл/м. Какую работу надо совершить, чтобы перенести заряд Q =6,7 нКл из центра полукольца в бесконечность?
38. Тонкий стержень согнут в кольцо радиусом R =10 см и заряжен с линейной плотностью τ =300 нКл/м. Какую работу надо совершить, чтобы перенести заряд Q =65 нКл из центра кольца в точку, расположенную на оси кольца на расстоянии r =20 см от его центра?
39. Две параллельные заряженные плоскости, поверхностные плотности заряда которых σ1 = 2 мкКл/м2, σ2 =- 0,8 мкКл/м2, находятся на расстоянии d =0,6 см друг от друга. Определить разность потенциалов между плоскостями.
40. Диполь с электрическим моментом р =100 пКл∙м свободно установился в электрическом поле напряженностью Е =200 кВ/м. Определить работу внешних сил, которую необходимо совершить для поворота диполя на угол α =180°.
41. Пылинка массой m =200 мкг, несущая на себе заряд Q =40 нКл, влетела в электрическое поле в направлении силовых линий. После прохождения разности потенциалов U =200 В пылинка имела скорость υ =10 м/с. Определить скорость υ0 пылинки до того, как она влетела в поле.
42. Какая ускоряющая разность потенциалов требуется для того, чтобы сообщить скорость υ =30 Мм/с: 1) электрону; 2) протону?
43. Найти отношение скоростей ионов Cu++ и К+, прошедших одинаковую разность потенциалов.
44. Протон, начальная скорость которого υ =100 км/с, влетел в однородное электрическое поле Е =300 В/см так, что вектор скорости совпал с направлением линий напряженности. Какой путь должен пройти протон в направлении линий поля, чтобы его скорость удвоилась?
45. Бесконечная плоскость заряжена отрицательно с поверхностной плотностью σ = 35,4 нКл/м2. По направлению силовой линии поля, созданного плоскостью, летит электрон. Определить минимальное расстояние, на которое может подойти к плоскости электрон, если на расстоянии l0 =5 см он имел кинетическую энергию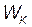 
=80 эВ.
46. Электрон с энергией 
=400 эВ (в бесконечности) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом R =10 см. Определить минимальное расстояние а, на которое приблизится электрон к поверхности сферы, если ее заряд Q = - 10 нКл.
47. Электрон влетел в плоский конденсатор, имея скорость υ =10 Мм/с, направленную параллельно пластинам. В момент вылета из конденсатора направление скорости электрона составляло угол α =35° с первоначальным направлением скорости. Определить разность потенциалов между пластинами (поле считать однородным), если длина пластин l =10 см и расстояние между ними d =2 см.
48. В однородное электрическое поле напряженностью Е =200 В/м влетает (вдоль силовой линии) электрон со скоростью υ0 =2 Мм/с. Определить расстояние, которое пройдет электрон до точки, в которой его скорость будет равна половине начальной.
49. Электрон движется вдоль силовой линии однородного электрического поля. В некоторой точке поля с потенциалом φ1 =100 В электрон имел скорость υ1 =6 Мм/с. Определить потенциал φ2 точки поля, дойдя до которой электрон потеряет половину своей скорости.
50. Пылинка массой m =5 нг, несущая на себе N =10 электронов, прошла в вакууме ускоряющую разность потенциалов U =1 МВ. Какова кинетическая энергия пылинки? Какую скорость приобрела пылинка?
51. Расстояние между обкладками плоского конденсатора равно d. Между ними находится пластинка из диэлектрика с диэлектрической проницаемостью ε1 =2,1толщиной d 1=4,5 мм. Напряжение на конденсаторе равно U0 =85 В. Если вынуть диэлектрик, то напряжение на конденсаторе станет равным U =110 В. Определить расстояние d.
52. Два шара радиусами R1 =0,5 см и R2 =1,1 см имели заряды Q1 = 5,4 нКл и Q2. После того, как шары соединили тонкой проволокой, их потенциалы стали одинаковыми и равными φ =0,67 кВ. Определить заряд Q2.
53. Два шара радиусами R1 =9,1 см и R2 =4,7 см имели заряды Q1 и Q2 =17 нКл. После того, как шары соединили тонкой проволокой, их потенциалы стали одинаковыми и равными φ = - 2,2 кВ. Определить заряд Q1.
54. У конденсаторов емкостью С1 =680 пФ и С2 =710 пФ, заряженных до напряжения U1 =400 В и U2 соответственно, соединили между собой разноименно заряженными обкладками. Напряжение на конденсаторах после соединения стало равным U = - 120 В. При разряде выделилась энергия W. Определить напряжение U2.
55. Напряженность поля заряженного плоского конденсатора с расстоянием между пластинами d =6 см равна Е =150 В/см. Параллельно пластинам в конденсатор вносится незаряженная металлическая пластина толщиной h =1,5 см. Найти разность потенциалов между обкладками конденсатора до и после внесения пластинки.
56. Два конденсатора емкостями С1 =5 мкФ и С2 =8 мкФ соединены последовательно и присоединены к батарее с ε =80 В. Определить заряды Q1 и Q2 конденсаторов и разности потенциалов U1 и U2 между обкладками.
57. Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектрика: слоем стекла толщиной d1 =0,2 см и слоем парафина толщиной d2 =0,3 см. Разность потенциалов между обкладками U =300 В. Определить напряженность поля и падение потенциала в каждом из слоев.
58. Плоский конденсатор состоит из двух круглых пластин радиусом R =10 см каждая. Расстояние между пластинами d =2 мм. Конденсатор присоединен к источнику напряжения U =80 В. Определить заряд и напряженность поля конденсатора в двух случаях: а) диэлектрик – воздух; б) диэлектрик – стекло.
59. Плоский конденсатор с площадью пластин S =200 см2 каждая заряжен до разности потенциалов U =2 кВ. Расстояние между пластинами d =2 см. Диэлектрик – стекло. Определить энергию W поля конденсатора и плотность ω энергии поля.
60. Два конденсатора емкостями С1 =2 мкФ и С2 =5 мкФ заряжены до напряжений U1 =100 В и U2 =150 В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими разноименные заряды.
61. Катушка и амперметр соединены последовательно и подключены к источнику тока. К клеммам катушки присоединен вольтметр с сопротивлением r =4 кОм. Амперметр показывает силу тока I =0,3 А, вольтметр – напряжение U =120 В. Определить сопротивление R катушки. Определить относительную погрешность, которая будет допущена при изменении сопротивления, если пренебречь силой тока, текущего через вольтметр.
62. ЭДС батареи ε =80 В, внутреннее сопротивление r = 5 Ом. Внешняя цепь потребляет мощность Р =100 Вт. Определить силу тока в цепи, напряжение, под которым находится внешняя цепь, и ее сопротивление.
63. Два источника с ЭДС ε1 =2,1 В и ε2 =1,5 В соединены одноименными полюсами и подключены к внешнему напряжению R =12 Ом. Внутреннее сопротивление источников r1 = 11 Ом и r2 = 15 Ом. Токи в ветвях цепи I1, I2, I3. Определить силу тока I в цепи.
64. Два источника с ЭДС ε1 =1,7 В и ε2 соединены одноименными полюсами и подключены к внешнему напряжению R =15 Ом. Внутреннее сопротивление источников r1 = 24 Ом и r2 = 33 Ом. Токи в ветвях цепи I1, I2, I3. Ток I2 =0,011 А. Определить ε2.
65. Батарея с ЭДС ε и внутренним сопротивлением r отдает во внешнюю цепь при токе I1 =5,1 А мощность Р1 =9,2 Вт, а при токе I2 =8,2 А мощность Р2 =14 Вт. Определить ЭДС ε.
66. Батарея с ЭДС ε и внутренним сопротивлением r =0,012 Ом отдает во внешнюю цепь при токе I1 =6,3 А мощность Р1 =10,8 Вт, а при токе I2 =3,9 А мощность Р2 =14 Вт. Определить мощность Р2.
67. При внешнем сопротивлении R1 =8 Ом сила тока в цепи I1 =0,8 А, при сопротивлении R2 =15 Ом сила тока в цепи I1 =0,5 А. Определить силу тока короткого замыкания источника ЭДС.
68. ЭДС батареи ε =24 В. Наибольшая сила тока, которую может дать батарея, Imax =10 А. Определить максимальную мощность Pmax, которая может выделиться во внешней цепи.
69. От источника с напряжением U =800 В необходимо передать потребителю мощность P =10 кВт на некоторое расстояние. Какое наибольшее сопротивление может иметь линия передачи, чтобы потери энергии в ней не превышали 10% от передаваемой мощности?
70. При включении электромотора в сеть с напряжением U =220 В он потребляет ток I =5 А. Определить мощность, потребляемую мотором, и его КПД, если сопротивление обмотки мотора равно R =6 Ом.
71. ЭДС батареи ε =12 В. При силе тока I =4 А КПД батареи η =0,6. Определить внутреннее сопротивление r батареи.
72. Сопротивление обмотки электродвигателя, изготовленной из медного провода, до начала работы при температуре t1 =20 ° С равно R1 =0,13 Ом, а по окончании работы R2 =0,13 Ом. Определить до какой температуры нагрелся двигатель во время работы.
73. Найти температуру нити вольфрамовой лампы накаливания в рабочем состоянии, если известно, что сопротивление нити в момент включения при температуре t1 =20 ° С в 12,6 раза меньше, чем в рабочем состоянии.
74. Шкала микроамперметра с внутренним сопротивлением r =10 Ом содержит 100 делений при цене деления 10 мкА. Найти сопротивление шунта, который необходимо присоединить к прибору, чтобы можно было измерять ток до I =1 А.
