На рис. 5.1, а показано сталевий вал постійного перерізу. Модуль пружності при зсуві G = 8·104МПа. Допустиме напруження при крученні [ 
] = 60 МПа. Допустимий відносний кут закручування [ 
] = 0,25 град/м.
Потрібно:
1) визначити значення скручувального моменту 
;
2) побудувати епюру крутних моментів М к;
3) за умовою міцності знайти діаметр d на кожній ділянці вала;
4) побудувати епюру відносних кутів закручування 
і провести перевірний розрахунок за умовою жорсткості.
Дані для розрахунку:
т = 2кН×м; а = 20 см;
Розв’язання.
1. Визначаємо значення скручувального моменту m 0:
, – т – т + m 0 –2 m = 0,
звідси m 0 = 4 m = 4 2 = 8,0 кН×м.
2. Розрахуємо значення скручувального моменту на кожній ділянці вала і будуємо епюру М к.
На ділянці I М к = – m = – 2 кН×м;
На ділянці II М к = – m – m = –2 m = – 4 кН×м;
На ділянці III М к = – m – m + 4 m = 2 m = 4 кН×м.
Рис. 5.1
За цими даними будуємо епюру М к (рис. 5.1, б).
3. За умовою міцності знаходимо діаметр вала d на кожній ділянці.
Умова міцності вала круглого поперечного перерізу при крученні має вигляд:
. (5.1)
Для круглого поперечного перерізу полярний момент опору 
визначається за формулою:
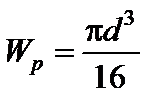. (5.2)
Із формули (5.1) випливає, що:
. (5.3)
Із співвідношення (5.2) маємо:
(5.4)
На ділянці І: М к = –2 кН×м. Отже, за формулою (5.3) маємо:
см3.
Із виразу (5.4) знаходимо:
d = 1,721 
=5,54 cм.
Беремо d = 5,6 см = 56 мм.
На ділянці ІІ: М к = –4,0 кН×м.
Отже,
.
d = 1,721 
.
Обираємо d = 7,0 см = 70 мм.
На ділянці ІІІ: М к = 4,0 кН×м. Отже, діаметр вала на третій ділянці потрібно взяти таким, як і на другій ділянці, тобто d = 70мм.
4. Будуємо епюру відносних кутів закручування і проводимо перевірку за умовою жорсткості, яка для вала круглого поперечного перерізу має вигляд:
.
Значення q визначаємо за формулами:
На ділянці І: М к = – 2,0 кН×м; d = 56 мм. Отже,
;
оскільки 1 радіан = 57,3°,
=1,48 град/м < [ 
] = 1,5 град/м,
тобто умова жорсткості на ділянці І виконується.
На ділянці ІІМ к = – 4,0 кН×м, d = 70 мм. Отже,
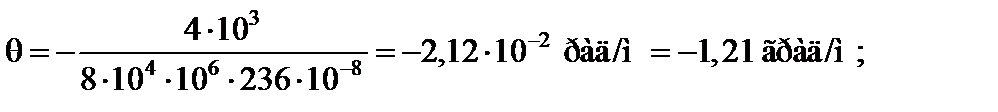
тобто умова жорсткості виконується.
На ділянці III: М к = 4,0 кН×м; d = 70 мм. Отже, q = 1,21 град/м. За цими даними будуємо епюру 
(рис. 5.1, в). Умова жорсткості на всіх ділянках вала виконується.
Методичні рекомендації
Під час вивчення кручення необхідно звернути увагу на закони розподілення напружень у разі розтягання (або стискання) і зсуву. Доцільно особливу увагу приділити побудові епюр крутних моментів, напружень і деформації — кутів закручування.
Необхідно запам’ятати, що при крученні виникає деформація чистого зсуву, а напружений стан – плоский. Потрібно вміти визначати головні напруження при крученні, встановлювати їх зв’язок з дотичними напруженнями, які виникають у поперечних перерізах вала. При виведенні формул для визначення напружень і деформації слід звернути увагу на використання спрощувальних гіпотез.
Вивчаючи питання про кручення бруса прямокутного поперечного перерізу, необхідно запам’ятати, що в цьому випадку поперечні перерізи не залишаються плоскими. Потрібно ознайомитися з формулами для визначення напружень у серединах сторін прямокутника: розглянути окремий випадок вузького прямокутного перерізу.
У процесі вивчення вільного кручення тонкостінних стержнів необхідно запам’ятати, що бруси відкритого і замкнутого профілів розраховуються по-різному. Слід ознайомитися з формулами для визначення максимального дотичного напруження і кутів закручування для відкритих перерізів, які складаються з вузьких і довгих прямокутників. Необхідно навчитися виводити подібні формули для бруса, який має поперечний переріз у формі замкнутого тонкостінного профілю.
Гвинтові пружини розраховують здебільшого на кручення. Потрібно навчитися виводити формули для найбільшого дотичного напруження і деформації пружини.
Запитання для самоперевірки
1. Що називається деформацією кручення? Який силовий фактор виникає в перерізі і як будується його епюра?
2. Виведіть формули для визначення напружень у поперечному перерізі і кута закручування круглого вала. Поясніть поняття «полярний момент інерції» і «полярний момент опору» перерізу.
3. Який напружений стан виникає в кожній точці круглого вала при крученні? Які напруження діють у поперечному і похилих до осі вала перерізах?
4. Як виконуються розрахунки вала на міцність і жорсткість? Доведіть, що порожнистий вал економніший за суцільний.
5. Виведіть формули для обчислення напружень і деформації в пружинах? На яких припущеннях основані виводи цих формул?
6. За якими формулами можна визначити дотичні напруження і кути закручування для бруса прямокутного поперечного перерізу?
7. На які два види поділяються тонкостінні профілі під час кручення?
8. Як визначаються дотичні напруження і кути закручування для тонкостінних стержнів відкритого і замкнутого профілів?
Складний опір
Розрахунок похилої балки
Для заданої похилої балки (рис. 6.1) потрібно:
1. Побудувати епюри поперечних сил Q, згинальних моментів М і нормальних сил N.
2. Підібрати переріз двотаврової балки.
3. Зробити перевірку за найбільшими нормальними та дотичними напруженнями.
Дані для розрахунку:
зосереджена сила P = 20 кН; вага погонного метру балки q =8 кН/м;вага від снігу q с= 6 кН/м; тиск вітру на один погонний метр балки q в= 5 кН/м; кут нахилу балки α = 250; довжина ділянок балки a = 1,5 м, b = 4 м; допустиме напруження 
МПа.
Рис. 6.1
І. Визначення навантаження, яке діє вздовж повздовжньої осі балки, а також навантаження, яке діє перпендикулярно поздовжній осі
а) від ваги снігу (рис. 6.2)
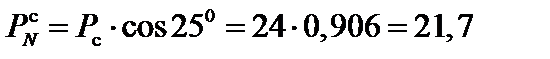кН;
кН;
кН.
Довжина ділянки балки, на яку діють сили 
і 
:
м.
Розподілене навантаження від ваги снігу на довжині ділянки балки 4,41 м (рис. 6.3).
кН/м;
кН/м.
б) Від зосередженої сили Р (рис. 6.4).
кН,
кН.
м, рис. 6.5).
кН/м;
кН/м.
На основі отриманих обчислень будуємо окремо розрахункову схему з врахуванням нормальних сил (рис. 6.6, а) і розрахункову схему з врахуванням тільки поздовжніх сил (рис. 6.6, г).
ІІ. Визначення опорних реакцій (рис. 6.6, а).
1. 
;
RB = 11,6 кН.
2. 
;
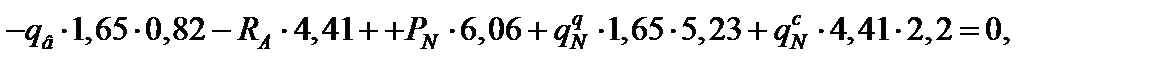
RA = 48,32 кН.
3. 
(перевірка). 
ІІІ. Побудова епюр Q і М (рис. 6.6, б, в).
І ділянка.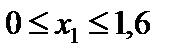 
м;
Рис. 6.6
.
При х 1 = 0 
х 1 = 1,65 м 
.
х 1 = 0 
.
х 1 = 1,65 м 
кН м;
ІІ ділянка. 1,65 м 
6,06 м;
.
При х 2 = 1,65 м 
18,32 кН;
х 2 = 6,06 м 
-3,35 кН.
Знаходимо координату х 2 в перерізі, де М max.
, звідси х 2 = 5,36 м.
При х 2 = 1,65 м 
31,23 кН×м.
х 2 = 6,06 м 
6,8 кН.м.
х 2 = 5,36 м 
6 кН×м.
ІІІ ділянка. (з правого боку) 
;
.
При х 3 = 0 м 
0 кН;
x 3 = 1,65 м 
8,25 кН.
.
При х 3 = 0 м 
кН·м.
х 3 = 1,65 м 
кН·м.
IV. Побудова епюри N (рис. 6.6, д).
Визначаємо опорну реакцію HA.
І ділянка. 0 
1,65 м; 
При х 1 = 0 
8,46 кН.
х 1 = 1,65 м 
кН.
ІІ ділянка. 1,65 м 6,06 м;
.
При х 2 = 1,65 м 
– 10,14 кН;
х 2 = 6,06 м 
0.
ІІІ ділянка.
.
V. Підбір поперечного перерізу двотаврової балки.
Побудувавши епюри М і N, бачимо, що небезпечним є переріз при х = 1,65 м, в якому М max = 31,23 кН·м і N = 14,03 кН·м;
МПа. (6.1)
Умова міцності (6.1) вміщує дві невідомих величини Wy i F. В більшості випадків напруження σ від згинання більше, ніж від поздовжньої сили, тому при підборі перерізу можна спочатку у формулі (6.1) опустити другий доданок і знайти наближене значення 
із розрахунку на згинання.
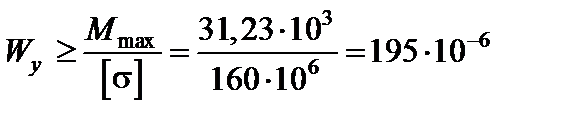м3 = 195 cм3.
Потім за таблицею сортаменту потрібно вибрати двотавр з моментом опору дещо більшим, ніж Wy.
Вибираємо двотавр №22 (ДСТУ 8239-89), Wy = 232 cм3,
F = 30,6 cм2.
Потім перевіряємо міцність вибраного перерізу, обчислюючи максимальне нормальне напруження за формулою (6.1).
= 138,5 МПа 
МПа.
Перевірка міцності балки за найбільшими дотичними напруженнями.
Для балки №22 за таблицями знаходимо:
S 0 = 131 cм3; Jy = 2550 cм4; b 0 = 0,54 cм.
Тут 
МПа.
Отже, умова міцності за найбільшими нормальними і дотичними напруженнями задовольняється.
