Короткі теоретичні відомості:
Якщо на балку будуть діяти декілька зосереджених моментів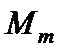 
, декілька зосереджених сил 
і декілька ділянок рівномірно розподіленого навантаження інтенсивністю 
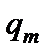(рис. 4.9),
Рис. 4.9
то рівняння зігнутої осі балки можна подати у такому вигляді:
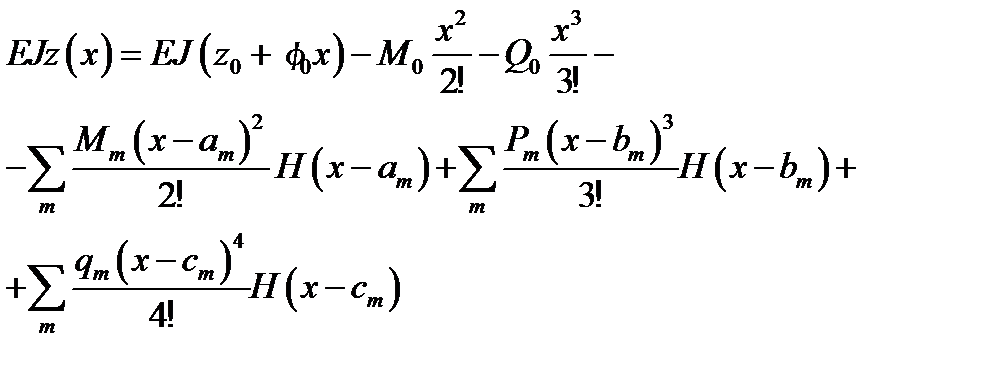(4.7)
де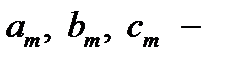 
абсциси точок прикладення зосереджених пар сил 
, сил 
відповідно, початків рівномірно розподілених навантажень інтенсивністю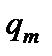 
. У формулі (4.7) припускається, що початок координат збігається з лівим кінцем балки.
Два початкових параметри із чотирьох у формулі (4.7) є відомими при будь-якому методі закріплення лівого кінця балки. Дійсно, для затиснутого лівого кінця 
і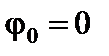 
для шарнірно-опертого лівого кінця 
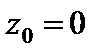і 
для вільного кінця відом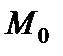і 
і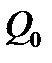 
. Невідомі один або два початкових параметри знаходять з умов закріплення інших перерізів балки.
Розглянемо приклади застосування методу початкових параметрів.
Приклад 1. Для балки, показаної на рис. 4.10 знайти рівняння прогинів і кутів повороту а також значення прогину і кута повороту перерізу в точці В.
;
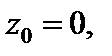
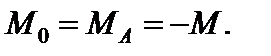
З урахуванням цього рівняння вираз (4.7) набуває вигляду:
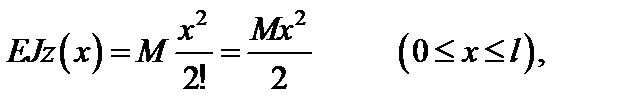
звідси:
.
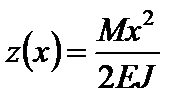
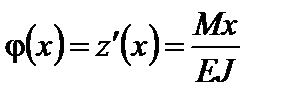
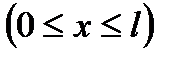При x = l маємо:
Приклад 2. Для заданої консольної балки знайти рівняння прогинів і кутів повороту, а також значення прогину і кута повороту перерізу в точці В (рис. 4.11).
Рис. 4.11
У цьому випадку початкові параметри дорівнюють:
.
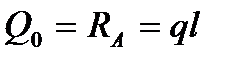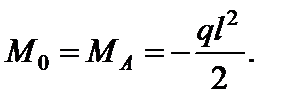
Отже, на основні рівняння (4.7) у даному випадку отримаємо:
;
.
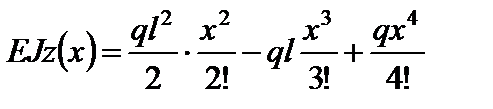
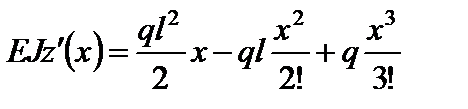
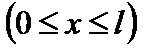Отже, остаточно одержуємо рівняння прогинів і кутів повороту перерізу:
;
.
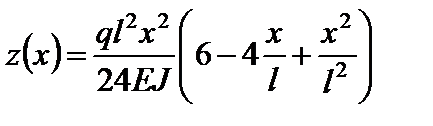
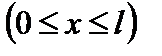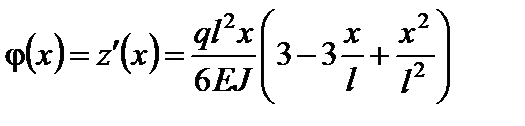
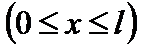При x = l маємо:
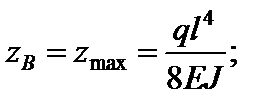
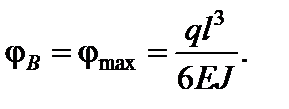
Приклад 3. Для балки на двох опорах знайти рівняння прогинів і кутів повороту, а також значення прогину в перерізі під силою Р (рис. 4.12).
Для балки, яка розглядається
,
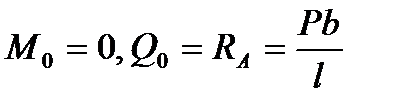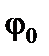– невідомо.
Для ділянки I 
:
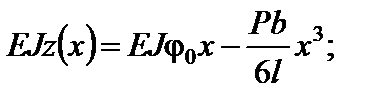
Рис. 4.12
для ділянки II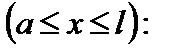 
Для визначення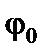 
використаємо умову: при x = l z = 0.
Отже,
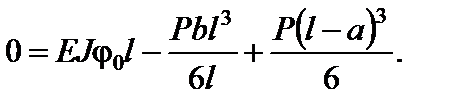
Звідси дістаємо
.
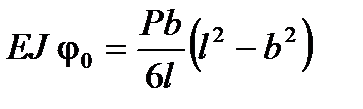Таким чином:
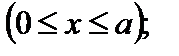
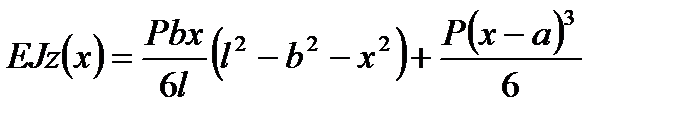
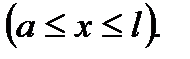
Визначаємо прогин перерізу під силою, тобто при x = a:
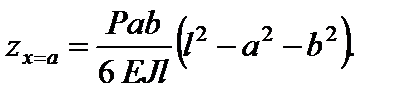
У тому окремому випадку, коли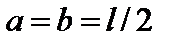 
, маємо:
Приклад 4. Застосуємо метод початкових параметрів до визначення переміщень в перерізах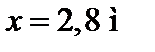 
і 
для балки, зображеної на рис. 4.13
Рис. 4.13
Дано: Р = 32 кН, q = 14 кН/м, m = 16 кНм.
(Балка двотавр №22 (ДСТУ 8239-89)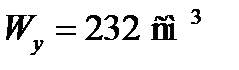 
, 
).
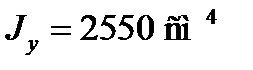Розв’язання: В даному випадку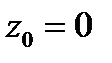 
, 
, 
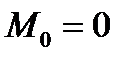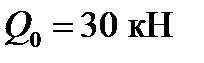. Невідомий початковий параметр 
.
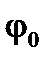Рівняння зігнутої осі балки буде мати вигляд:
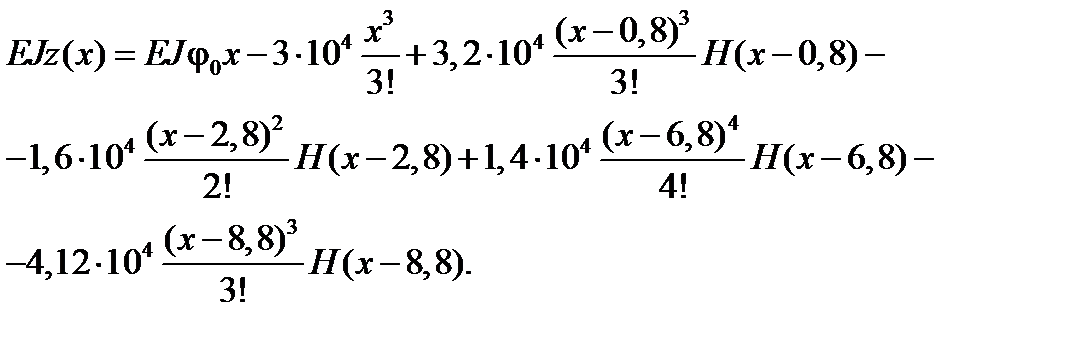
Невідомий початковий параметр 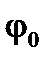можна визначити із умови на опорі В, при x =8,8 м. z=0. На відрізку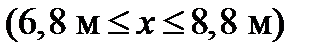 
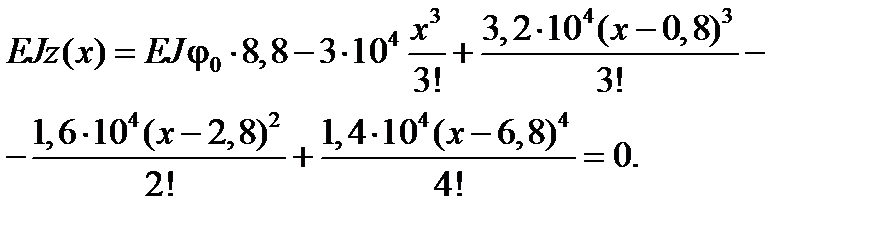
Задовольняючи умову на опорі В, отримаємо рівняння
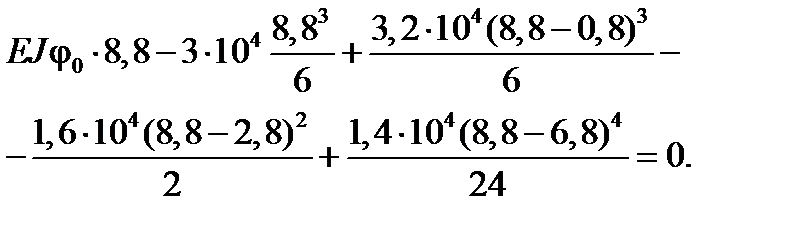
Звідси
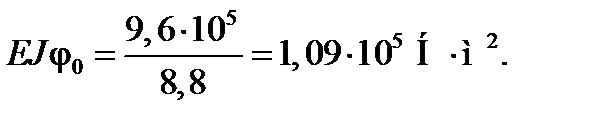
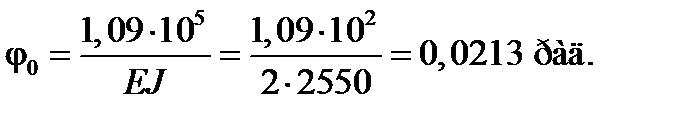
Підставляючи знайдене значення 
у рівняння зігнутої осі балки, дістаємо остаточне рівняння у такому вигляді:
для ділянки I 
;
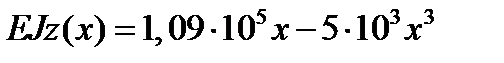для ділянки II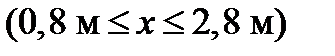 
;
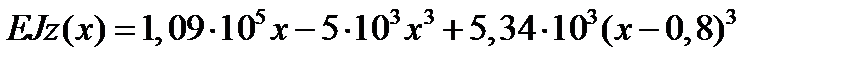для ділянки III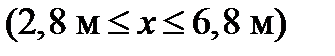 
;
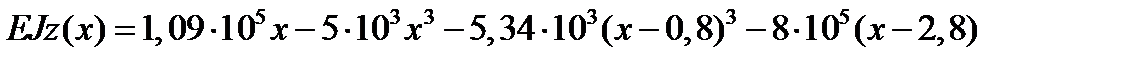для ділянки IV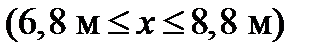 
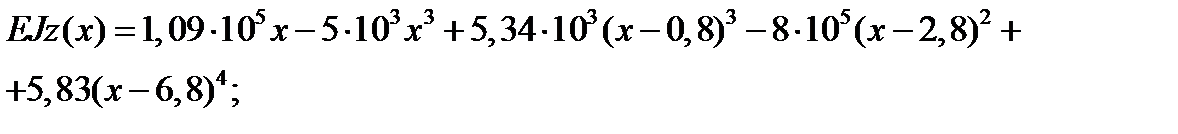для ділянки V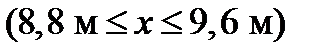 
За допомогою цих рівнянь можна визначити прогин у будь-якому перерізі балки. Розрахуємо, наприклад, прогини балки в перерізах при x =2,8 м та x =6,8 м.
Використовуючи рівняння II-ї ділянки, маємо:
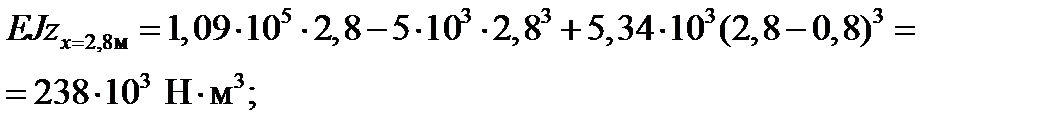
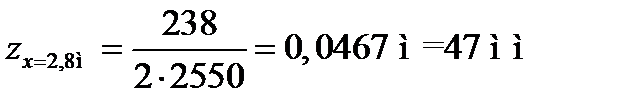
Використовуючи рівняння III-ї ділянки, маємо:
.
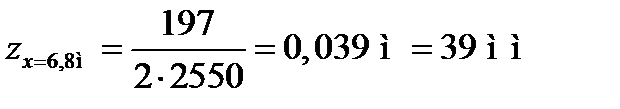