Для балки двотаврового перерізу, яка піддається косому згинанню (рис. 6.7, а, в). Потрібно:
1) підібрати двотавровий переріз;
2) знайти положення нейтральної осі;
3) визначити нормальне напруження 
у точках А, В, С і D небезпечного перерізу балки.
Дані для розрахунку:
Р = 18 кН; l = 3 м; m 0 = 5 кН×м;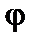 
= 30°; 
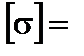160 МПа.
Розв’язання:
1. Підбираємо двотавровий переріз балки. Спочатку будуємо епюру згинальних моментів М (рис. 6.7, б). Маємо:
М mах = 11,0 кН×м.
Умова міцності для двотаврового перерізу при косому згинанні має вигляд:
.
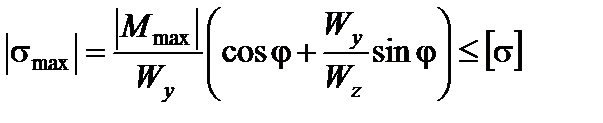Рис. 6.7
Звідси знаходимо:
.
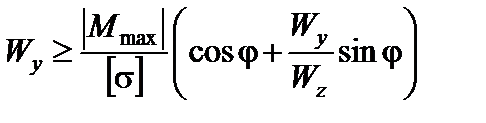Оскільки невідомі дві величини, а саме 
і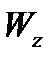 
, то необхідно задатися відношенням / 
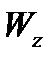. Це відношення для двотаврів дорівнює 6,1...13,5. Тому в першому наближенні візьмемо / 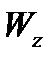= 10.
Враховуючи, що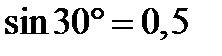 
; 
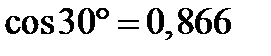, маємо:
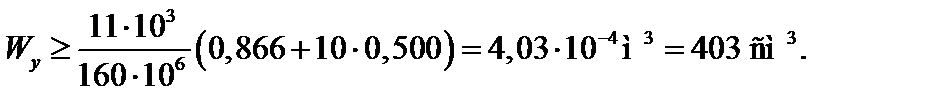
Візьмемо в першому наближенні: двотавр №27 а;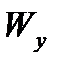 
= 407 см3; 
= 50,0 см3.
Перевіряємо виконання умови міцності
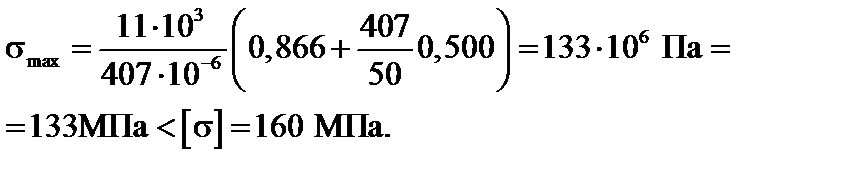
Оскільки було отримано недонапруження, то беремо двотавр №27; 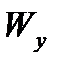= 371 см3; = 41,5 см3. У цьому випадку
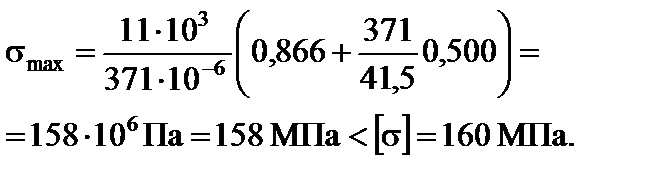
Остаточно візьмемо: двотавр № 27 (ДСТУ 8239-89);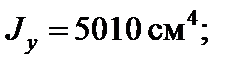 
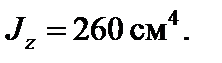
2. Знаходимо положення нейтральної осі. Маємо:
Оскільки tg 30° = 0,577, то отримуємо
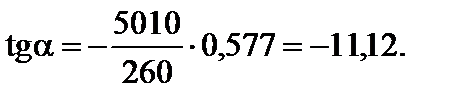
Отже,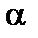 
= –84,9°. Знак «мінус» вказує на те, що кут 
у цьому випадку треба відкладати від осі у проти ходу годинникової стрілки. Нейтральну вісь показано на рис. 6.7, в.
3. Визначаємо нормальне напруження в точках А, В, С і D небезпечного перерізу балки.
Нормальне напруження в будь-якій точці небезпечного перерізу в цьому випадку можна визначити за формулою
Згинальний момент має місце в перерізі балки, де прикладена сила Р; цей переріз і буде небезпечним. Маємо:
.
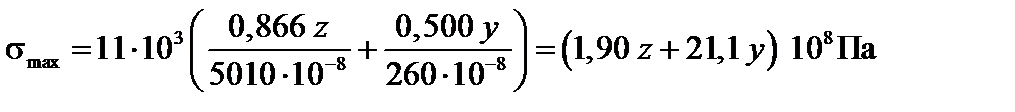Для двотавра №27 ширина полиці b = 125 мм, висота двотавра h= 270 мм. Тому координати точок А, B, С і D будуть мати такі значення:
А (6,25; 13,5); В (–6,25; 13,5);
С (6,25; –13,5); D (–6,25; –13,5).
Координати точок вказані в сантиметрах.
Отже,
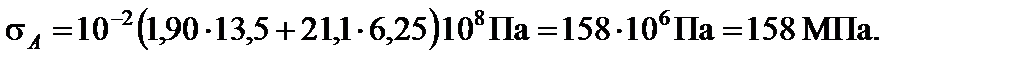
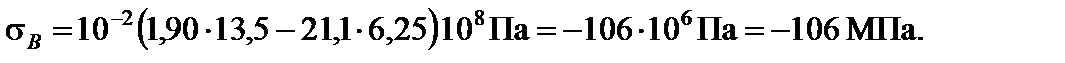
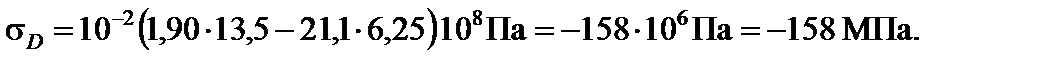
Визначення ядра перерізу
Приклад 1. П р я м о к у т н и й переріз (рис. 6.8).
У цьому випадку квадрати радіусів інерції дорівнюють:
; 
.
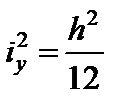За формулами
; 
, 
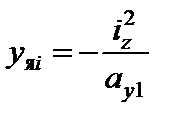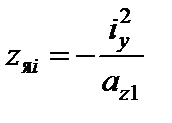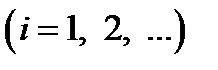(6.2)
; 
;
; 
.
Координати точок 3 і 4 неважко знайти з умови симетрії. З’єднуючи отримані точки 1, 2, 3 і 4 прямими лініями, отримаємо контур ядра перерізу (рис. 6.8).
Приклад 2. Круглий переріз (рис. 6.9). Маємо:
.
; 
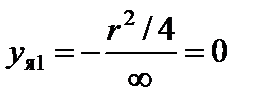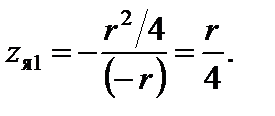
Зважаючи на симетрію контуром ядра перерізу буде коло радіусом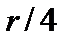 
(рис. 6.9).
Приклад 3. Двотавровий переріз (рис. 6.10). За формулами (6.2) знаходимо координати точок 1 і 2, які належать контуру ядра перерізу:
; 
.
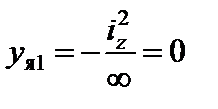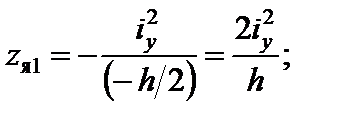
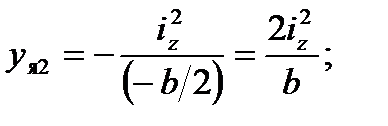
Координати точок 3 і 4 можуть бути знайдені з умови симетрії.
Позацентрове розтягання
Стальний стержень довжиною l = 1,5 м піддається позацентровому розтяганню. Поперечний переріз стержня зображено на рис. 6.11. Стержень розтягується поздовжніми силами Р, прикладеними в кінцевих перерізах у точці С.
Потрібно:
1) визначити необхідні геометричні характеристики поперечного перерізу стержня;
2) знайти відрізки, що відсікаються нейтральною віссю на осях координат;
3) обчислити нормальне напруження σ в точках А, В, С і D та побудувати епюру зміни цього напруження вздовж сторін перерізу.
Дані для розрахунку: Р = 50 кН, b = 5 см, h = 6 см, d = 4см.
Розв’язання.
1. Визначаємо необхідні геометричні характеристики поперечного перерізу стержня.
Площа перерізу:
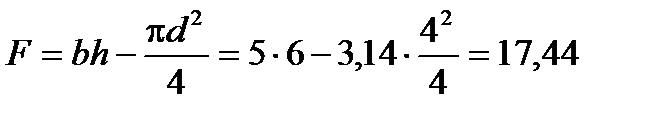см2.
Рис. 6.11
Осьові моменти інерції перерізу:
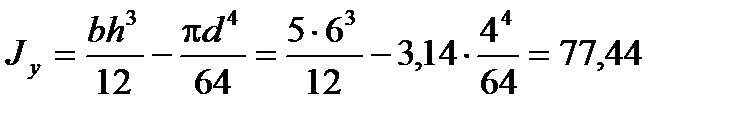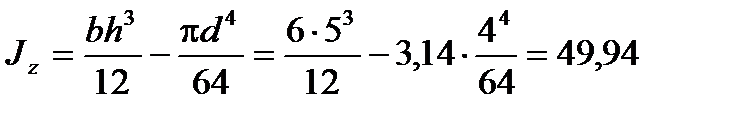см4;
см4.
Квадрати радіусів інерції перерізу:
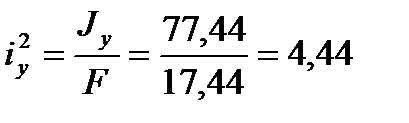см2; 
см2.
2. Знаходимо відрізки, які відсікаються нейтральною віссю на осях координат. Ці відрізки можна визначити за формулами:
; 
,
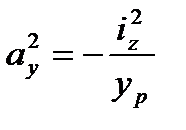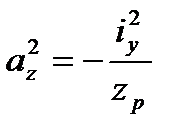де 
– координати точки перетину лінії дії сил Р з площею поперечного перерізу стержня.
Маємо: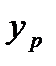 
= 2,5 см; zр = 3,0 cм.
Отже,
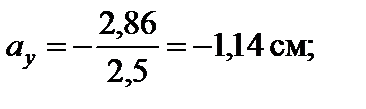
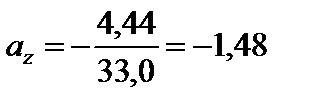см.
За цими даними проводимо нейтральну вісь (рис. 6.11).
3. Обчислюємо нормальне напруження в точках А, В, С і D та будуємо епюру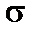 
.
Нормальне напруження в будь-якій точці поперечного перерізу стержня при позацентровому розтяганні можна визначити за формулою
.
Тут у, z – координати точки перетину, в якій визначається напруження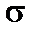 
. Координати точок А, В, С і D такі: А (–2,5; –3,0), В (2,5; –3,0), С(2,5; 3,0), D (–2,5; 3,0). Координати вказані в сантиметрах. Отже, маємо:
У цій формулі координати y і z взяті в метрах.
Таким чином,
;
;
;
.
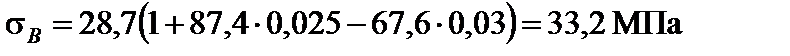За цими даними будуємо епюру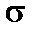 
вздовж сторін поперечного перерізу стержня (рис. 6.11). Найбільше розтягальне напруження має місце в точці С, а найбільше стискальне – у точці А.
