Підібрати діаметр вала постійного перерізу (рис. 6.19, а). Для розрахунків використати теорію міцності потенціальної енергії формозмінення. Матеріал валу сталь марки 40Х. 
800 МПа, 
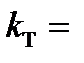1,5.
Дані для розрахунку:
Сила Р = 12 кН; вага шківів і зубчастого колеса:
G 1 = 1,0 кН; G 2 = 0,75 кН; G 3 = 0,5 кН; діаметри: D 1 = 40 см; D 2 = 30 см; D 3 = 25 см; = 30;
Розв’язання.
1. Визначаємо значення сили Р 1. Для цього складаємо рівняння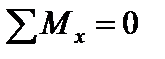 
, де х поздовжня вісь вала. Маємо:
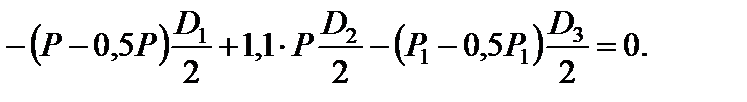
Підставляючи в це рівняння числові значення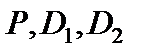 
і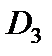 
, отримаємо:
.
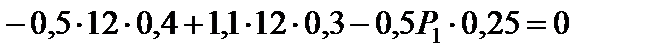Звідси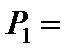 
12,5 кН.
2. Будуємо епюру згинальних моментів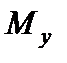 
, які діють у вертикальній площині. Сили 
, 
, 
, 
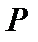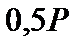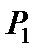і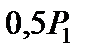 
переносимо паралельно самим собі до поздовжньої осі вала. Потім сили 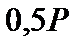, і 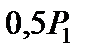розкладаємо на вертикальні й горизонтальні складові. Вертикальні сили (
), 
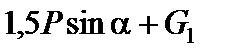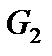і (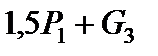
).
Маємо (рис. 6.19, б):
у перерізі С: 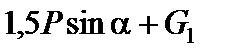= 1,5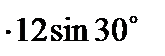 
+ 1,0 = 10 кН;
у перерізі D: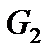 
= 0,75 кН;
у перерізі Е: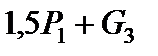 
= 1,5 12,5 + 0,5 = 19,25 кН.
Визначаємо вертикальні опорні реакці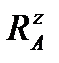ї 
і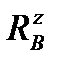 
:
, 
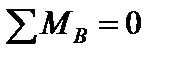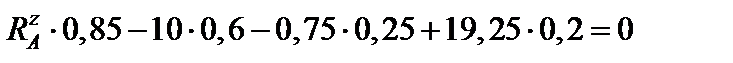
звідси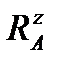 
= 2,75 кН;
Рис. 6.19
, 
,
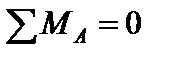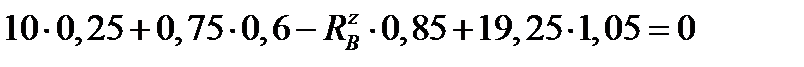звідси 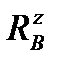=27,25 кН.
Перевірка:
;
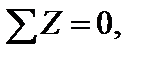
2,75 + 27,25 30 = 0, 0 = 0.
Розрахуємо згинальні моменти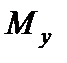 
для поперечних перерізів А, В, С, D, Е, 
;
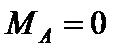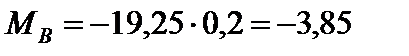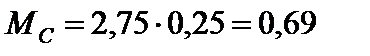кН×м;
кН×м;
кН×м;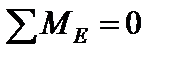 
.
За цими даними будуємо епюру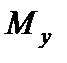 
(рис. 6.19, в).
3. Будуємо епюру згинальних моментів 
, які діють у горизонтальній площині. Маємо такі горизонтальні сили (рис. 6.19, г):
у перерізі С: 
= 1,5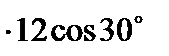 
= 18 0,866 = 15,59 кН;
у перерізі D; 1,1 Р = 1,1 
= 13,2 кН.
Визначаємо горизонтальні опорні реакції 
і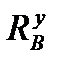 
:
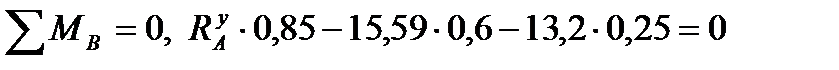
звідси = 14,88 кН;
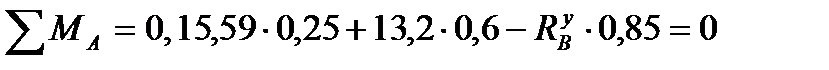
звідси 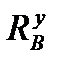= 13,91 кН.
Перевірка:
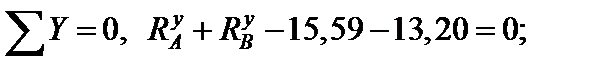
14,88 + 13,91 28,79 = 0; 28,79 28,79 = 0; 0 = 0.
Визначаємо згинальні моменти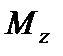 
для поперечних перерізів А, В, С, D, Е:
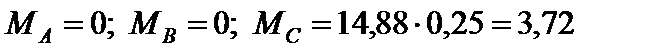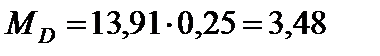кН×м;
кН×м;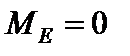 
.
За цими даними будуємо епюру (рис. 6.19, д).
4. Будуємо епюру повних згинальних моментів М. Повний згинальний момент у будь-якому поперечному перерізі вала може бути визначений за формулою
.
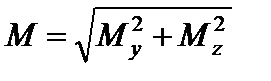Для поперечних перерізів А, В, С, D, Е. Маємо:
кН×м;
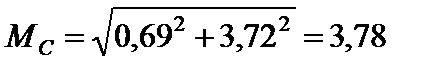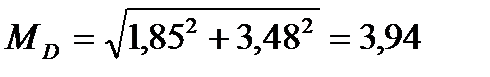кН×м;
кН×м; .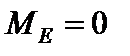
За отриманими даними будуємо епюру повних згинальних моментів М (рис. 6.19, е). Площини дії цих моментів у різних перерізах вала різні, але відповідні ординати епюри умовно сумісні з площиною рисунка. На тих ділянках вала, де прямі, які обмежують епюри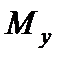 
і 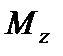, перетинають осі епюр у точках, розташованих на одній вертикалі, епюра М обмежена прямими, а на решті ділянок вона обмежена кривими (рис. 6.19, е).
5. Будуємо епюру крутних моментів М к, яка при сумісній дії згинання і кручення будується так само, як і при чистому крученні.
У перерізах С і Е, де розташовані шківи, і в перерізі D,де насаджено зубчасте колесо, слід прикласти зовнішні скручувальні моменти. Маємо:
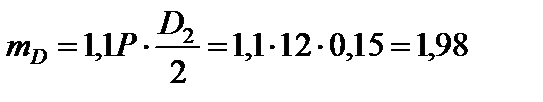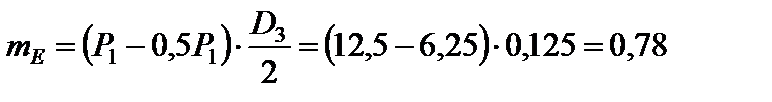кН×м;
кН×м.
Ці скручувальні моменти прикладаємо в перерізах С, D і Е вала (рис. 6.19, ж). За цими даними будуємо епюру крутних моментів М к, (рис. 6.19, з).
6. Визначаємо небезпечний переріз вала, який встановлюється на основі епюр М і М к. У цьому випадку небезпечним буде переріз D при х = 0,6 – 0. У цьому перерізі
М = 3,94 кНм; М к = 1,20 кНм.
7. Знаходимо діаметр вала. Умова міцності при сумісному згинанні і крученні за четвертою теорією міцності має вигляд:
.
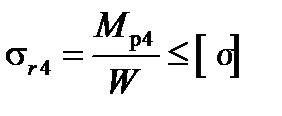Тут 
– розрахункове напруження за четвертою теорією міцності;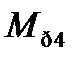 
– розрахунковий (приведений) момент за четвертою теорією міцності; W осьовий момент опору поперечного перерізу вала; 
– допустиме напруження.
Отже,
.
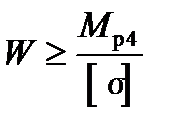За цією формулою можна розрахувати діаметр вала. Спочатку знаходимо:
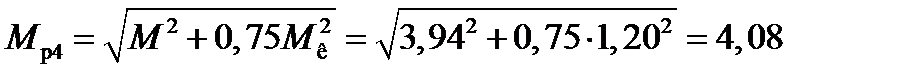кН×м;
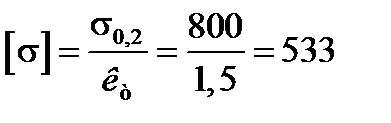МПа.
Таким чином,
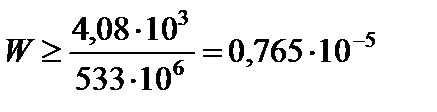м3 = 7,65 см3.
Для вала круглого поперечного перерізу
,
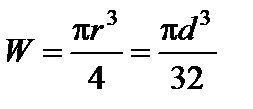де r радіус вала; d діаметр вала.
Отже,
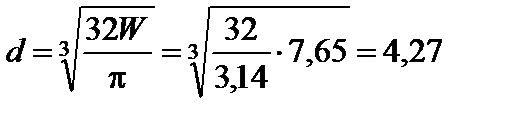см.
Візьмемо остаточно d = 4,30 см.
Методичні рекомендації
Перед вивченням цього розділу рекомендується повторити прості види деформації: розтягання (стискання), кручення і згинання. Потім слід розібратися в методиці виведення розрахункових формул, зрозуміти принцип незалежності дії сил і умови його застосування.
Вивчення складного опору починають з косого згинання. Нейтральна лінія при косому згинанні вже не перпендикулярна до площини зовнішніх сил, а площина, у якій розташовані прогини при косому згинанні, не збігається з площиною зовнішніх сил. Напруження і деформації при косому згинанні визначаються як сума (алгебрична або геометрична) відповідних значень, які визначені для двох плоских згинань відносно головних осей інерції.
Потрібно пам’ятати, що розрахункові формули у випадку позацентрового розтягання (стискання) виведені в системі координат, які збігаються з головними центральними осями інерції. Тому при розв’язанні задач обов’язково треба знаходити положення центра ваги перерізу і головних осей інерції й визначати геометричні характеристики перерізу відносно цих осей.
При позацентровому прикладенні стискальної сили в перерізі можуть виникати розтягальні напруження. Отже, позацентрове стискання особливо небезпечне для стержнів, виготовлених із крихких матеріалів (цегла, бетон), які чинять незначний опір розтягальним напруженням. У зв’язку з цим необхідно звернути увагу на визначення і побудову ядра перерізу.
Під час вивчення сумісної дії згинання і кручення важливо запам’ятати, який напружений стан виникає в матеріалі і чому при розрахунках необхідно використовувати теорії міцності.
Запитання для самоперевірки
1. Який випадок згинання називається косим?
2. В яких точках поперечного перерізу виникають найбільші напруження при косому згинанні?
3. Як знаходять положення нейтральної лінії при косому згинанні?
4. Як визначають деформації при косому згинанні?
5. Чи може балка з круглим поперечним перерізом сприймати косе згинання?
6. Як знаходять напруження в будь-якій точці поперечного перерізу при позацентровому розтяганні й стисканні?
7. Чому дорівнює напруження в центрі ваги поперечного перерізу при позацентровому розтяганні й стисканні?
8. Яке положення займає нейтральна вісь, коли поздовжня сила прикладена до вершини ядра перерізу?
9. Яке напруження виникає в поперечному перерізі стержня при згинанні з крученням?
10. Як знаходять небезпечні перерізи стержня при згинанні з крученням?
11. В яких точках круглого поперечного перерізу виникають найбільші напруження при згинанні з крученням?
12. Чому зазвичай не враховують дотичні напруження від згинання при сумісній дії згинання з крученням?
13. Як знаходять розрахунковий момент при згинанні з крученням стержня з круглим поперечним перерізом?
14. За якою теорією міцності (третьою або четвертою) отримаують більший розрахунковий момент при заданих значеннях моментів М і М к?
Тонкостінні стержні
