Для заданого тонкостінного стержня (поперечний переріз якого показано на рис. 7.1) потрібно:
- визначити центр ваги, положення головних центральних осей і підрахувати головні моменти інерції;
- визначити центр згинання і головний секторіальний момент інерції;
- від стискальної сили Р, прикладеної в точці Б перерізу, побудувати епюри нормальних напружень в долях Р;від осьової поздовжньої сили N; від моменту Му; від моменту Мz; від бімоменту В;
- побудувати сумарну епюру нормальних напружень у частинах Р;
- визначити допустиму стискальну силу Р і побудувати кінцеву епюру нормальних напружень.
1. Унаслідок симетрії перерізу, центр ваги лежить на осі симетрії у, а сама вісь у є головною центральною віссю. Довільно проводимо вісь z 1. Координата центра ваги перерізу:
Рис. 7.1 (розміри в сантиметрах).
 ;
;
 см3;
см3;
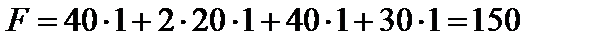 см2;
см2;
 см.
см.
Визначаємо моменти інерції відносно осей у та z (у, z – головні, центральні осі інерції):
 см4;
см4;

Отже, маємо
 .
.
2. Секторіальна площа являє собою подвійну площу, описану радіусом-вектором РА під час руху точки А по контуру від початку відліку О до деякого значення дуги s. Якщо радіус-вектор обертається за годинниковою стрілкою, приріст площі має знак «плюс», а якщо проти – «мінус». Секторіальна площа вимірюється в квадратних сантиметрах. Ця площа залежить від початку відліку і положення полюса:
 .
.
Будуємо епюру секторіальної площі 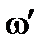 при довільно вибраному полюсі
при довільно вибраному полюсі 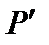 (рис 7.2).
(рис 7.2).
Початок відліку дуги s потрібно вибирати так, щоб виконувалась умова:
 . (а)
. (а)
Якщо є вісь симетрії, то початок відліку О 1потрібно розмістити на цій осі симетрії. У цьому випадку умова (а) буде виконана. Епюру 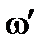 показано на рис. 7.3.
показано на рис. 7.3.
Будуємо також епюри y та z, тобто закони зміни відстаней точок контуру від осей y i z (рис. 7.4 і 7.5).
Координати центра згинання:
 ;
;  .
.
Рис. 7.2 Рис. 7.3
Розміри в сантиметрах
Рис. 7.4 Рис. 7.5
Оскільки товщина контуру  стала, то
стала, то  . У цьому випадку:
. У цьому випадку:
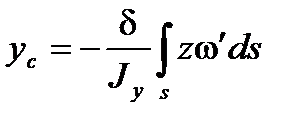 ;
;  .
.
Для обчислення інтегралів, які входять у ці формули, можна користуватись правилом Верещагіна.
Розраховуємо:
 см4;
см4;

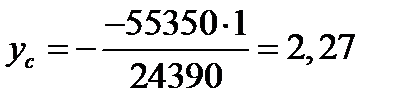 см;
см;

Відрізки yc і zc відкладаються від полюса  в напрямку головних центральних осей y i z (рис. 7.6).
в напрямку головних центральних осей y i z (рис. 7.6).
Рис. 7.6
Тепер будуємо епюру головної секторіальної площі  при центрі згинання P як при головному секторіальному полюсі.
при центрі згинання P як при головному секторіальному полюсі.
Використовуємо співвідношення:
 .
.
Тут:  – секторіальна площа при полюсі
– секторіальна площа при полюсі  ;
;  – те саме при полюсі
– те саме при полюсі  y, z i
y, z i 
 – координати точок s і
– координати точок s і 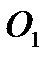 в системі координат y, z; а, b – координати полюса
в системі координат y, z; а, b – координати полюса  в системі координат
в системі координат 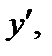
 , що має початок у точці
, що має початок у точці  і паралельні осям y i z.
і паралельні осям y i z.
У цьому випадку:

 см;
см; 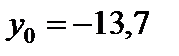 см,
см,  = 0.
= 0.
Отже,

За цією формулою будуємо епюру головної секторіальної площі  (рис. 7.7).
(рис. 7.7).
Точка 1.  ;
;
Точка 2.  см2;
см2;
Точка 3.  см2;
см2;
Точка 4.  см2;
см2;
Точка 5.  см2;
см2;
Рис. 7.7
Точка 6. 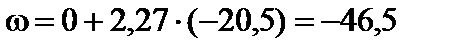 см2;
см2;
Точка 7. 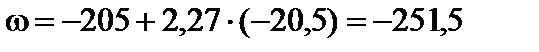 см2;
см2;
Точка 8.  см2;
см2;
Точка 9.  ;
;
Точка 10.  см2.
см2.
Визначаємо головний секторіальний момент інерції перерізу:

 см6.
см6.
3. Якщо сила  стискає, то напруження в будь-якій точці перерізу визначаються за формулою:
стискає, то напруження в будь-якій точці перерізу визначаються за формулою:
 .
.
Уцьому випадку бімомент 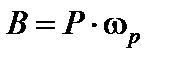 , отже:
, отже:
 ,
,
де  ,
,  ,
,  – ординати епюр
– ординати епюр 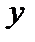 ,
,  ,
,  у точці прикладення сили
у точці прикладення сили  .
.
У нашому випадку:
 см2,
см2,  см4,
см4,  см4,
см4,
 см6;
см6;  см;
см;  см;
см;
 см2;
см2; 
Отже,

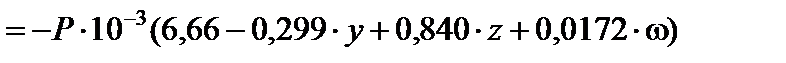 .
.
Використовуючи цю формулу, будуємо епюри напружень  ,
,  ,
,  і
і  (рис. 7.8–7.11). Потім будуємо сумарну епюру
(рис. 7.8–7.11). Потім будуємо сумарну епюру  (рис. 7.12).
(рис. 7.12).
Рис. 7.8 Рис. 7.9
Рис.7.10 Рис.7.11
| Ординати всіх епюр (Рис. 7.8-7.12) необхідно помножити на 10-3 P/см2 |
Рис.7.12
Точка 1.

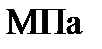 .
.
Точка 2.

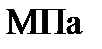 .
.
Точка 3.

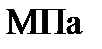 .
.
Точка 4.

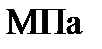 .
.
Точка 5.
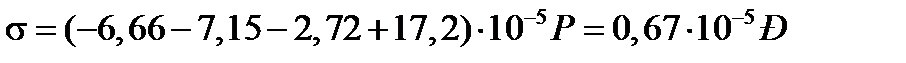
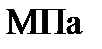 .
.
Точка 6.
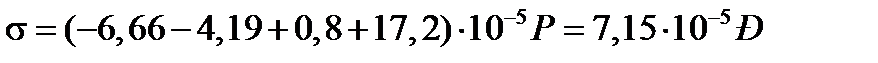
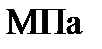 .
.
Точка 7.

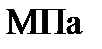 .
.
Точка 8.

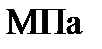 .
.
Точка 9.

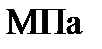 .
.
Точка 10.
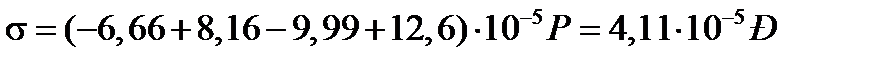
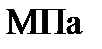 .
.
В формулах для визначення напруження  в точках 1-10 сила Р виражена в Ньютонах (Н).
в точках 1-10 сила Р виражена в Ньютонах (Н).
4. Найбільше за абсолютною величиною напруження 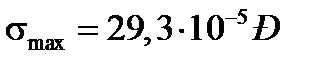
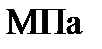 .
.
За умовою міцності  МПа.
МПа.
Отже,  . Звідси
. Звідси
 .
.
Будуємо кінцеву епюру нормальних напружень (від сили
Р = 546 кН), (рис. 7.13).
Рис 7.13
Методичні рекомендації
Під час вивчення цього розділу потрібно відразу усвідомити, який стержень є тонкостінним. При деформації тонкостінного стержня поперечний переріз не залишається плоским – проходить депланація перерізу. Слід більш чітко розібратися, що являє собою депланація перерізу. Необхідно навчитися також визначати секторіальну площу і секторіальні характеристики тонкостінних перерізів. Потрібно вміти визначати дотичні напруження при поперечному згинанні тонкостінних стержнів. Варто звернути особливу увагу на поняття «центр згинання» та вміти визначати депланацію поперечних перерізів тонкостінного стержня при крученні. Розібратися в питаннях стисненого кручення тонкостінних стержнів відкритого профілю. Слід також розглянути загальні випадки навантаження тонкостінного стержня і ознайомитися з поняттям «бімомент».
Запитання для самоперевірки
1. Який стержень називається тонкостінним?
2. Що таке депланація перерізу тонкостінного стержня?
3. Які існують секторіальні характеристики тонкостінних перерізів і як вони визначаються?
4. Що таке центр згинання і як визначається його положення?
5. Напишіть формулу для визначення нормального напруження в поперечному перерізі тонкостінного стержня з урахуванням бімоменту?






