Для балки, зображеної на рис. 4.4, а, потрібно:
1) визначити опорні реакції;
2) побудувати епюру поперечних сил Q;
3) побудувати епюру згинальних моментів М;
4) підібрати двотавровий поперечний переріз;
5) перевірити міцність балки за найбільшими нормальними напруженнями;
6) перевірити міцність балки за найбільшими дотичними напруженнями;
7) побудувати епюри напружень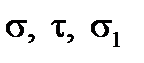 
і 
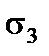у тому перерізі балки, де очікується найбільше значення головного напруження;
8) визначити положення головних площадок;
9) перевірити міцність балки за головними напруженнями, використовуючи четверту теорію міцності.
Дані для розрахунку: Р = 16 кН, q = 12 кН/м, m = 5 кНм, = 160 МПа.
Розв’язання.
1. Визначаємо опорні реакці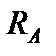ї 
і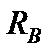 
, для чого складаємо суму моментів усіх зовнішніх сил відносно точки А (точки В) і прирівнюємо її до нуля. Маємо:
.
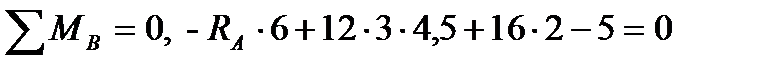Звідси знаходимо: 
;
,
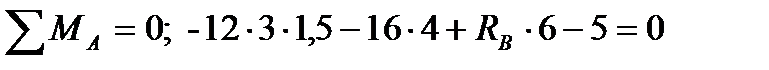отже,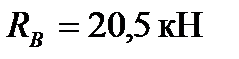 
.
Перевірка:
.
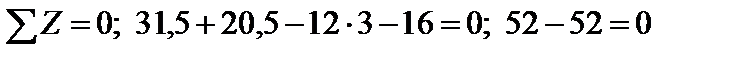2. Визначаємо поперечну силу і будуємо епюру Q. Спочатку балку розбиваємо на ділянки I, II, III і IV.
На ділянці I (0 х 3 м):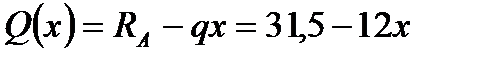 
.
При х = 0 Q = 31,5 кН, при х = 3 м Q = 31,5 12 3 = 4,5 кН.
На ділянці II (3 м х 4 м):
.
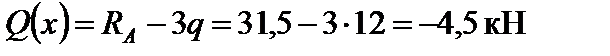На ділянці III (4 м х 6 м):
.
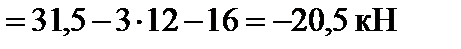На ділянці IV (6 м х 7 м):
.
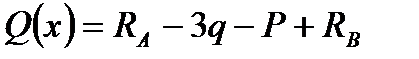
Рис. 4.4
За цими даними будуємо епюру Q (рис. 4.4, б).
3. Визначаємо згинальний момент і будуємо епюру М.
На ділянці I (0 х 3 м): 
.
При х = 0 М = 0, при х = 3 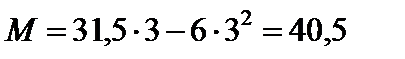м 
кН×м.
Визначаємо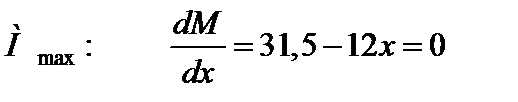 
, звідси х = 2,625 м.
Отже,
.
На ділянці II (3 м х 4 м):
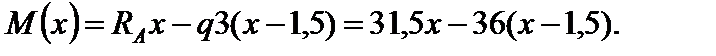
При х = 3 м М = 31,5 3 36 1,5 = 40,5кН×м;
при х = 4м М = 31,5 4 36 2,5 = 36,0кН×м.
На ділянці III (4 м х 6 м):
.
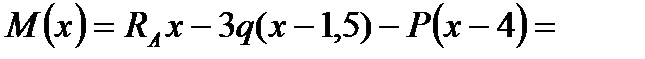
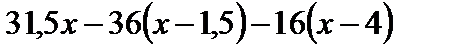При х = 4 м М = 31,5 4 36 2,5 = 36,0кНм,
при х = 6 м М = 31,5 6 36 4,5 16 2 = 5 кНм.
На ділянці IV (6 м х 7 м):
.
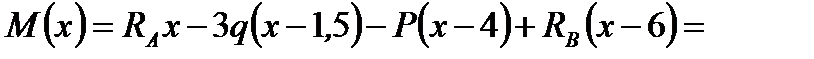
За цими даними будуємо епюру М (рис. 4.4, в).
4. Підбираємо двотавровий переріз балки. Для цього використовуємо формулу
.
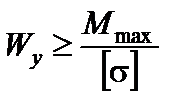Найбільший згинальний момент 
буде в перерізі 
. 
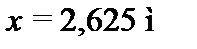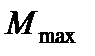= 41,35 кНм, 
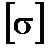= 160 МПа. Отже,
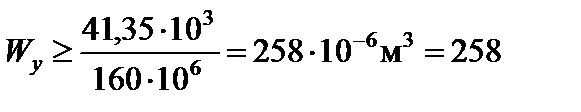см3.
Обираємо двотавр № 
з 
см3.
5. Перевіряємо міцність балки за найбільшими нормальними напруженнями. Умова міцності за найбільшими нормальними напруженнями має вигляд:
.
У цьому випадку маємо
.
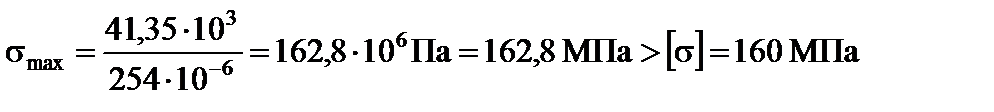Умова міцності не виконується. Перенапруження становить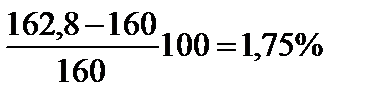 
, що допустимо.
6. Перевіряємо міцність балки за найбільшими дотичними напруженнями. Умова міцності за найбільшими дотичними напруженнями має вигляд:
,
тут 
– статичний момент відносно нейтральної осі частини перерізу, яка лежить нижче (вище) нейтральної осі; 
ширина перерізу балки на нейтральній осі.
Для стальних балок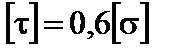 
. Отже,
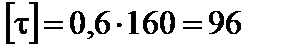МПа.
Таким чином, для двотавра № 22 а
.
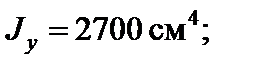
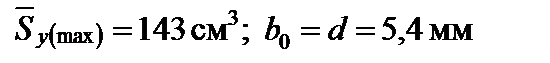Найбільша поперечна сила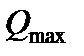 
буде в перерізі х = 0; 
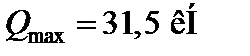. Отже,
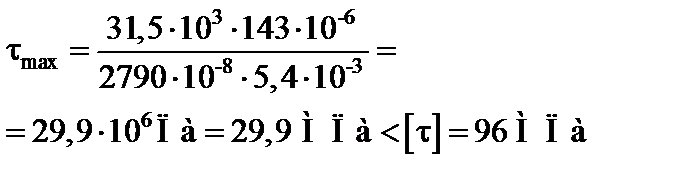
тобто умова міцності за найбільшими дотичними напруженнями виконується.
7. Визначаємо напруження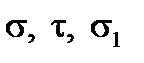 
і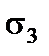 
у тому перерізі балки, де очікуються найбільші значення головних напружень.
Для перевірки міцності за головними напруженнями візьмемо переріз х = (4 + 0) м, у якому М = 36,0 кНм, Q = 20,5 кН.
Нормальні й дотичні напруження визначаємо за формулами:
.
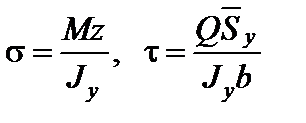Головні напруження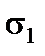 
і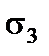 
визначаємо за формулою
.
Напруження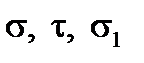 
і 
визначаємо в точках 1, 2, 3, 4, а в точках 1', 2', 3' аналогічно (рис. 4.5).
У точці 1:
;
;
.
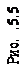
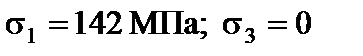У точці 2:
;
;
.
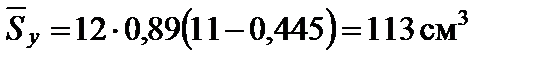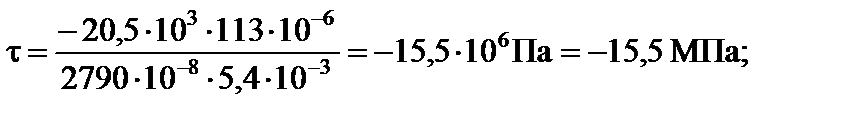
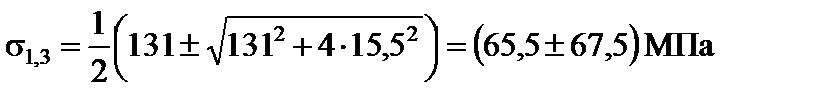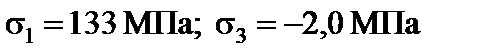У точці 3:
;
;
;
.
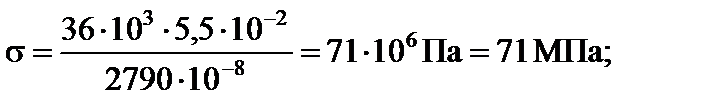
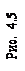
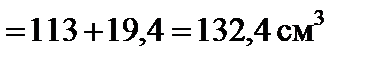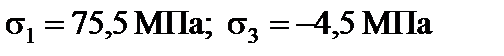У точці 4:
;
;
.
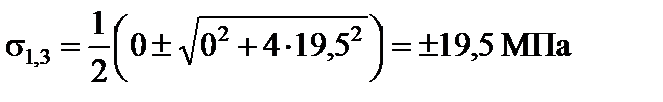За цими даними будуємо епюри 
у перерізі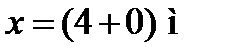 
(рис. 4.5).
8. Визначаємо положення головних площадок за формулою:
.
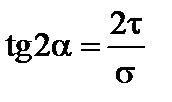У точці 1:
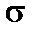= 142 МПа; 
; 
; 
.
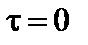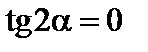У точці 2:
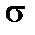= 131 МПа; 
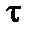= –15,5 МПа;
; 
.
У точці 3:
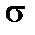= 71 МПа; 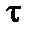= –18,1 МПа;
; 
.
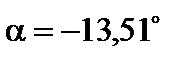У точці 4:
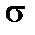= 0 МПа; 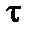= –19,5 МПа;
; 
.
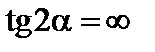У точці 3 ¢:
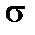= – 71 МПа; 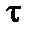= –18,1 МПа;
; 
.
У точці 2 ¢:
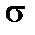= –131 МПа; 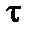= –15,5 МПа;
; 
.
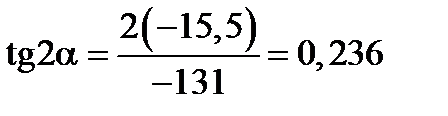У точці 1 ¢:
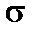= –142 МПа; ; ; .
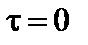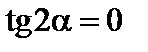Положення головних площадок показано на рис. 4.6.
9. Перевіряємо міцність балки за головними напруженнями, використовуючи четверту теорію міцності.
Умова міцності за четвертою теорією міцності (теорією найбільшої потенціальної енергії зміни форми) має вигляд:
,
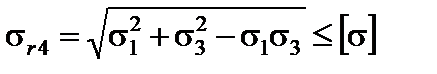де 
розрахункове напруження за четвертою теорією міцності.
Як видно з рис. 4.6, виконувати перевірку міцності за головними напруженнями слід у точці 1. У цій точці: 
; 
.
Отже,
,
тобто умова міцності за головними напруженнями в заданому перерізі виконується.
Рис. 4.6
