Дослідження напруженого стану в точці

Навколо деякої точки напруженого тіла виділений елемент
(рис. 2.1, а).

а б

Рис. 2.1

Потрібно:

1) виконати перепозначення напружень відповідно до правил опору матеріалів;

2) визначити головні напруження;

3) знайти положення головних площадок і показати лінії дії головних напружень;

4) визначити значення найбільших дотичних напружень і показати площадки, на яких вони діють;

5) виконати перевірку міцності матеріалів;

Дані для розрахунку:

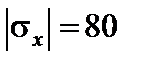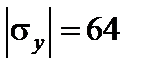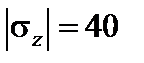МПа; МПа; МПа;

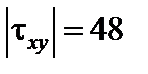МПа; матеріал - сталь Ст. 30; 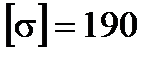МПа.

Розв’язання:

1. Перепозначаємо напруження по гранях паралелепіпеда за правилами опору матеріалів. При цьому має бути .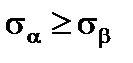

Дамо напруженням нові позначення, які діють не на головних площадках (рис. 2.1, б). Отже, маємо:

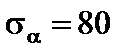МПа; МП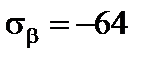а;

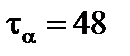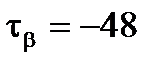МПа; МПа.

2. Визначаємо значення головних напружень. Головні напруження нумеруємо так, щоб виконувалась умова 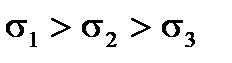. Значення головних напружень знаходимо за формулою

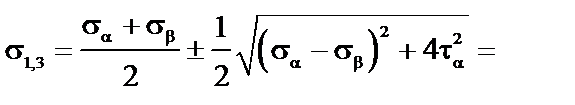
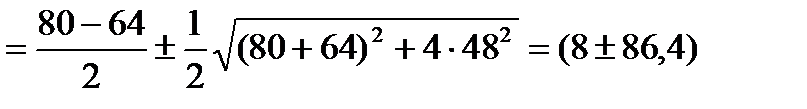МПа.

Отже,

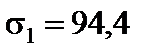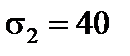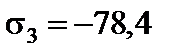МПа, МПа, МПа.

3. Розрахуємо положення головних площадок. Для цього використовуємо формулу

.

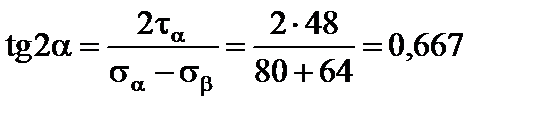Отже, , .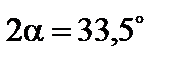

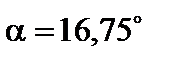Положення головних площадок і лінії дії головних напружень зображені на рис. 2.2. Щоб отримати лінію дії головного напруження , потрібно від лінії дії напруження 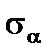відкласти кут за ходом годинникової стрілки (якщо кут додатний).

4. Знаходимо значення найбільшого дотичного напруження 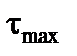за формулою

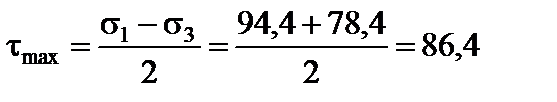МПа.

Щоб отримати напрямок нормалі до площадки, на якій діє напруження 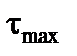, треба від напрямку головного напруження відкласти кут 45 проти ходу годинникової стрілки (рис. 2.2).

 

5. Виконаємо перевірку міцності матеріалу використовуючи третю теорію міцності. Маємо:

.

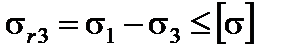У цьому випадку:

,

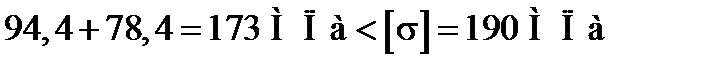тобто умова міцності за третьою теорією міцності виконується. Для сталі Ст. 30 залишкове відносне подовження при розриві = 21 %. Тому цей матеріал є пластичним і для перевірки його міцності можна скористатися третьою теорією міцності.

Рис. 2.2

 

Методичні рекомендації

Головні напруження відіграють важливу роль у процесі розв’язання задачі про міцність матеріалу: одне з цих напружень є найбільшим, а друге – найменшим з усіх нормальних напружень для заданої точки.

Важливо встановити, коли виникають лінійний, плоский або об’ємний напружені стани. Слід навчитися доводити закон парності дотичних напружень, установлювати зв’язок між головними напруженнями і напруженнями, які виникають на двох довільних взаємно перпендикулярних площадках.

Слід звернути увагу на виведення узагальнюючого закону Гука.

Необхідно приділити особливу увагу суті теорії міцності, з’ясувати, чому теорії міцності не використовуються при лінійному напруженому стані, за результатами яких випробувань встановлюють допустимі напруження. Важливо зрозуміти, що при складному напруженому стані розрахунок ведеться за еквівалентним напруженням, яке залежить від прийнятої теорії міцності.

Запитання для самоперевірки

1. Які є види напруженого стану матеріалу?

2. У чому полягає закон парності дотичних напружень?

3. Чому дорівнює сума нормальних напружень на двох взаємно перпендикулярних площадках?

4. На яких площадках виникають найбільші й найменші нормальні напруження?

5. Чому дорівнює найбільше дотичне напруження у випадку плоского напруженого стану?

6. Як знаходять деформації при плоскому і об’ємному напружених станах?

7. Як формулюються перша і друга теорії міцності?

8. Як знаходять розрахункове напруження за третьою і четвертою теоріями міцності?