Бетонна колона піддається дії сил Р 1 і Р 2 (рис.6.12, а). На (рис.6.12, б) показані точки перетину К 1 і К 2 ліній дії сил Р 1 і Р 2 з площиною перерізів 1–1 і 2–2.
Припускається, що висота колони (Н 1+ Н 2) така, що гнучкість λ не перевищує 40, тобто λ≤40.
Потрібно:
1). визначити нормальні напруження в перерізах 1–1 і 2–2 колони;
2). показати ядро перерізу, побудувати епюри нормальних напружень σ для перерізів 1–1 і 2–2;
3). перевірити виконання умови міцності за найбільшими стискаючими та розтягуючими напруженнями.
Рис. 6.12
Дані для розрахунку:
P 1 = 225,0 кН; P 2 = 450,0 кН; К 1(8; –7); К 2(14; 8); h 1 = 30 см; b 1 = 30 см; h 2 = 30 см; b 2 = 60 см; [σP] = 5 МПа; [σс] = 20 МПа. (Координати точок наведені в сантиметрах).
Розв’язання.
Бетона колона працює на позацентрове стискання.
Напруження σ в даному випадку визначаються за формулою:
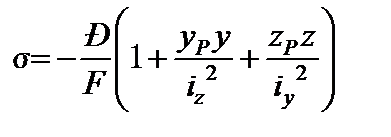, (6.3)
де Р - сила, з якою стискається колона; F - площа поперечного перерізу; 
, 
- координати точки перетину лінії дії сили Р з площиною поперечного перерізу F бруса; 
, 
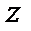- координати точок перерізу, в яких визначаються напруження σ; 
, 
- квадрати радіусів інерції.
1. Визначаємо необхідні геометричні характеристики поперечного перерізу 1–1 бруса.
Площа перерізу: F1 = b 1 h 1 = 30 ∙ 30 = 900 см2.
Квадрати радіусів інерції перерізу:
см2;
см2.
2. Знаходимо відрізки, які відсікає нейтральна вісь на осях координат. За формулами:
; 
, (6.4)
де yp, zp – координати точки перетину лінії дії сили Р 1 з площиною поперечного перерізу 1–1 брусу.
Маємо: yp = 8 см; zp = –7 см.
Отже, за формулами (6.4) знаходимо:
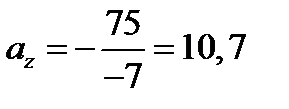см; 
см.
За цими даними проводимо нейтральну вісь (рис. 6.13).
Рис. 6.13
3. Обчислюємо нормальні напруження в точках А 1, В 1, С 1, D 1.
Нормальне напруження в будь-якій точці поперечного перерізу бруса при позацентровому стисканні можна визначити за формулою (6.3):
Координати точок А 1, В 1, С 1і D 1в яких визначаються напруження σ такі: А 1(15; –15); В 1(15; 15); С 1(–15; 15); D 1(–15; –15). Координати точок вказані в сантиметрах.
Отже, використовуючи формулу (6.3), маємо:
В цій формулі координати у, z потрібно підставляти в метрах.
Таким чином:
МПа;
МПа;
МПа;
МПа.
За цими даними будуємо епюри σ вздовж сторін поперечного перерізу бруса (рис. 6.13).
Найбільше стискаюче напруження має місце в точці А 1, а найбільше розтягуючи напруження в точці С 1.
При визначенні напружень отримуємо:
МПа < [σр] = 5 МПа;
МПа < [σс] = 25 МПа.
4. Побудова ядра перерізу.
Для побудови ядра перерізу (рис. 6.14) будемо задаватися різними положеннями нейтральної вісі, дотичними до контуру перерізу, й обчислювати координати відповідних точок прикладання сили Р 1 за такими формулами:
; 
. (6.5)
Рис. 6.14
Обчислені координати визначають точки, що лежать на межі ядра перерізу.
Сумістимо спочатку нейтральну вісь зі стороною А 1 В 1 (положення 11-11). В цьому разі:
см; 
Тоді з формул (6.5) маємо:
см; 
.
Отже, координати точки 1 ядра перерізу 1–1 визначені.
Сумістимо тепер нейтральну вісь із стороною А 1 D 1 (положення 21–21). Маємо:
; 
см.
Тоді координати точки 2 ядра:
; 
см.
Аналогічно визначаються координати точок 3 і 4, що відповідають положенням 31–31 та 41–41 нейтральної вісі.
5. Визначаємо необхідні геометричні характеристики поперечного перерізу бруса 2–2.
Площа перерізу:
Fz = b2h2 = 60 ∙ 30 = 1800 см2.
Квадрати радіусів інерції перерізу:
см2;
см2.
6. Знаходимо відрізки, які відсікає нейтральна вісь на осях координат у, z від дії сили Р 1. Ці відрізки можна знайти за формулами (6.4).
У формулі (6.4) уР, zР – координати точки перетину лінії дії сили Р 1 з площиною поперечного перерізу 2–2.
Маємо уР = 8 см; zР = –7 см. Отже, за формулами (6.4) знаходимо:
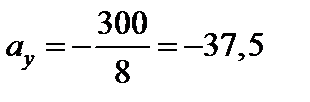см; 
см.
За цими даними проводимо нейтральну вісь (рис. 6.15).
7. Обчислюємоз нормальні напруження в точках А 2, В 2, С 2і D 2 за формулою (6.3).
Координати точок А 2, В 2, С 2і D 2, в яких визначаються напруження σ такі: А 2(30; –15); В 2(30; 15); С 2(–30; 15); D 2(–30; –15). Координати точок вказані в сантиметрах.
Отже, використовуючи формулу (6.3), маємо:
В цій формулі координати у і z потрібно підставляти в метрах.
Таким чином:
МПа;
МПа;
МПа;
МПа.
За цими даними будуємо епюру σ вздовж сторін поперечного перерізу бруса (рис. 6.15).
Рис. 6.15
Найбільше стискаюче напруження від сили Р 1 в перерізі 2–2 має місце в точці А 2, а найбільше розтягуючи напруження в точці С 2.
8. Побудова ядра перерізу 2–2.
Сумістимо спочатку нейтральну вісь зі стороною А 2 В 2 (положення 12-12) (рис.6.16).
Рис. 6.16
В цьому разі:
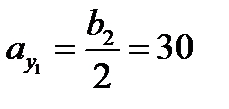см;
Тоді за формулами (6.5):
см; 
.
Отже, координати точки 1 ядра перерізу 2–2 визначені.
Сумістимо тепер нейтральну вісь із стороною А 2 D 2 (положення 22–22). Маємо:
см.
Тоді координати точки 2 ядра:
; 
см.
Аналогічно визначаються координати точок 3 і 4, що відповідають положенням 32–32 та 42–42 нейтральних осей.
9. Знаходимо відрізки, які відсікає нейтральна вісь на осях координат y, z перерізу 2–2 при дії сили Р 2.
Ці відрізки можна знайти за формулами (6.4):
де y p, z p – координати точки перетину лінії дії сили Р 2 з площиною поперечного перерізу 2–2 брусу.
Маємо: yp = 14 см; zp = 8 см.
Отже, за формулами (6.4) знаходимо:
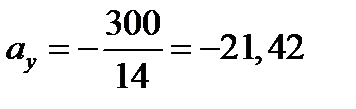см; 
см.
За цими даними проводимо нейтральну вісь (рис.6.17).
Рис. 6.17
10. Обчислюємо нормальні напруження 
в точках А 2, В 2, С 2, D 2 перерізу 2–2 від дії сили Р 2 (координати цих точок наведені в пункті 7). 
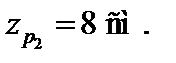
Використовуючи формулу (6.3), маємо:
В цій формулі координати у і z потрібно підставляти в метрах.
Таким чином:
МПа;
МПа;
МПа;
МПа.
За цими даними будуємо епюру σ вздовж сторін поперечного перерізу 2–2 бруса (рис. 6.17).
Найбільше стискаюче напруження від дії сили Р 2 в перерізі
2-2 має місце в точці В 2, а найбільше розтягуюче напруження - в точці D 2.
11. Визначаємо нормальні напруження в точках А 2, В 2, С 2і D 2 перерізу 2–2 при сумісній дії сил Р 1 і Р 2. Маємо:
МПа;
МПа;
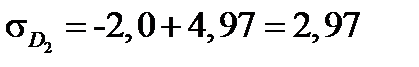МПа;
МПа.
За цими даними будуємо епюру σ вздовж сторін поперечного перерізу 2–2 бруса (рис. 6.18).
Найбільше стискаюче напруження від сумісної дії сил Р 1 і Р 2 в перерізі 2–2 має місце в точці В 2, а найбільше розтягуюче напруження в точці D 2.
При визначенні напружень отримуємо:
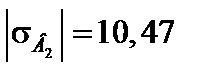МПа < [σс] = 25 МПа;
МПа < [σР] = 5 МПа.
Таким чином умова міцності бруса при стисканні силами Р 1 і Р 2 забезпечена.
Рис.6.18
