ДОХОДНІСТЬ ФІНАНСОВИХ ОПЕРАЦІЙ. На фінансовому ринку інвестора цікавить результат його операцій. Результативність інвестицій порівнюють за допомогою такого показника, як доходність.
Доходність – це відносний показник, що показує, який відсоток приносить 1 гривня інвестованих коштів за певний період.
Доходність за період. Доходність за період - це доходність, яку інвестор одержить за певний період часу. Вона визначається за формулою:
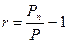(4.34)
де: r - доходність за період;
Р - початково інвестовані кошти;
Рn сума, одержана через n років.
Доходність з розрахунку на рік. На фінансовому ринку виникає необхідність порівнювати доходності різних фінансових інструментів. Тому показником доходності, що зустрічається найчастіше, є доходність в розрахунку на рік. Він визначається як середнє геометричне, а саме:
(4.34)
де: r - доходність в розрахунку на рік;
n - число років.
Розрахунок доходності при нарахуванні відсотків m разів за рік:
(4.35)
Якщо відсоток нараховується безперервно, то доходність в розрахунку на рік можна визначити за формулою:
(4.36)
де: rn - доходність, виражена як відсоток, що нараховується безперервно.
До цього часу ми визначали показник доходності за операціями, які тривали більше року. Тому розрахунки здійснювались за формулами з використанням складного відсотку. Коли фінансова операція триває менше року, в розрахунках, як правило, оперують простим відсотком. Якщо бути більш точним, то більш суворим критерієм в цьому випадку виступає можливість на практиці інвестувати кошти з врахуванням складного відсотку.
Для короткострокових операцій доходність визначається на підставі формул:
або 
(4.37)
Для короткострокових цінних паперів також можна розрахувати ефективну доходність, тобто ефективний відсоток. Для цього можна скористатися наступною формулою (для прикладу візьмемо фінансовий рік, що дорівнює 360 дням).
(4.38)
де: rеф - ефективна доходність в розрахунку на рік;
t - період фінансової операції (час з моменту купівлі до продажу або погашення цінного паперу);
r - простий відсоток в розрахунку на рік;
г, - доходність за період t.
Відсоткові ставки та інфляція. Нерідко ринковій економіці властива інфляція. Тому для відсоткових ставок (відповідно для показника доходності) необхідно розрізняти номінальні і реальні величини, щоб визначити діючу ефективність фінансових операцій. Якщо темп інфляції перевищує ставку відсотку, яку одержує вкладник на інвестовані кошти, то для нього результат від фінансової операції виявиться негативним. Не дивлячись на те, що за абсолютною величиною (в грошових одиницях, наприклад, в гривнях) його кошти збільшаться, їх сукупна купівельна спроможність зменшиться. Таким чином, він зможе купити на нову суму грошей менше товарів та послуг, ніж на ті кошти, якими володів до початку операції.
Номінальна відсоткова ставка - це відсоткова ставка без врахування інфляції. В якості номінальних виступають відсоткові ставки банківських установ. Номінальна ставка свідчить про абсолютне зростання грошових коштів інвестора.
Реальна відсоткова ставка - це ставка, що скоригована на відсоток інфляції. Реальна ставка свідчить про приріст купівельної спроможності коштів інвестора.
Взаємозв'язок між номінальною і реальною відсотковими ставками можна представити наступним чином:
(4.39)
Вищенаведене рівняння називають рівнянням Фішера. Запишемо його в літерному позначенні:
1 + r = (1 + y)*(1 + i) (4.40)
де: r - номінальна ставка відсотку;
у - реальна ставка відсотку;
і - темп інфляції.
З рівняння (4.20) можна одержати реальну відсоткову ставку:
або 
(4.41)
ОЦІНКА ФІНАНСОВИХ АКТИВІВ дозволяє прийнятиуправлінські рішення. Оцінка облігацій з купоном. Грошовий потік в цьому випадку складається з однакових за роками надходжень (С) і номінальної вартості облігації (М), які сплачуються в момент погашення.
(4.42)
Оцінка звичайних акцій з рівномірно зростаючими дивідендами. Ціну звичайних акцій з постійними темпами приросту дивідендів знаходять, спираючись на загальну схему оцінки фінансових активів, тобто шляхом складання дисконтованих грошових надходжень від володіння акцією.
(4.43)
Ця формула має зміст при r > g і носить назву моделі Гордона. Відмітимо, що показники r і g в формулах беруться в частках одиниці.
Визначення вартості дисконтного векселя. Дисконтні векселі котируються па підставі ставки дисконту. Вона говорить про величину знижки, яку продавець надає покупцю. Ставка дисконту вказується у відсотках до номіналу векселя як простий відсоток в розрахунку на рік. Ставку дисконту можна перерахувати в грошовий еквівалент за допомогою формули:
(4.44)
де: D - дисконт векселя;
N - номінал векселя;
d - ставка дисконту;
t - число днів з моменту придбання векселя до його погашення.
В знаменнику зазначається 360 днів, оскільки розрахунки з векселем здійснюються на базі фінансового року, який становить 360 днів.
Ставка дисконту визначається за формулою:
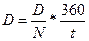(4.45)
Визначення ціни векселя. Ціну векселя можна визначити, вирахувавши з номіналу величину знижки, а саме:
P = N – D (4.46)
де: Р - ціна векселя.
Якщо відома ставка дисконту, то ціна визначається за формулою:
(4.47)
Якщо інвестор визначив для себе значення доходності, яку б він бажав забезпечити по векселю, то ціну паперу можна розрахувати за формулою:
(4.48)
де: r -доходність, яку бажає забезпечити собі інвестор. (Якщо вкладник порівнює інвестиції у вексель з іншими паперами, для яких фінансовий рік становить 365 днів, то у формулі доцільно в знаменнику ставити цифру 365).
Визначення суми нарахованих відсотків і вексельної суми за процентним векселем. За процентним векселем нараховуються відсотки за ставкою, яка зазначається у векселі. Суму нарахованих відсотків можна визначити за формулою:
(4.49)
де: І - сума нарахованих відсотків;
N - номінал векселя;
С% - відсоткова ставка, що нараховується за векселем;
ts - кількість днів від початку нарахування відсотку до його погашення.
Загальна сума, яку власник процентного векселя отримає при його погашенні, дорівнює сумі нарахованих відсотків і номіналу, її можна визначити за формулою:
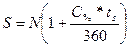(4.50)
де: S - сума відсотків і номіналу векселя.
Визначення ціни векселя. Ціна векселя визначається за формулою:
(4.51)
де: Р - ціна векселя;
І - кількість днів від купівлі до погашення векселя;
r - доходність, яку бажав би забезпечити собі інвестор.
Визначення суми нарахованих відсотків і суми погашення банківського сертифікату. При погашенні сертифікату інвестор одержить суму нарахованих відсотків, яка визначається за формулою:
(4.52)
де: N - номінал сертифікату;
t - строк, на який випущено сертифікат.
Розрахунок відсотків за сертифікатом. Загальну суму, яку одержить вкладник при погашенні сертифікату, можна визначити за формулою:
(4.53)
Визначення ціни сертифікату. Ціна сертифікату визначається за формулою:
(4.54)
де: Р ціна сертифіката;
t - кількість днів з моменту купівлі до погашення сертифікату;
r - доходність, яку бажав би забезпечити собі інвестор.
КОНТРОЛЬНІ ПИТАННЯ
1. Які фактори визначають зміну вартості грошей у часі?
2. Назвіть основні способи нарахування відсотків.
3. У чому полягає сутність еквівалентного і ефективного відсотків?
4. Що таке ануїтет?
5. Як розраховується доходність фінансових операцій за період?
6. Як враховують вплив інфляції на доходність фінансових операцій?
7. Як визначається вартість дисконтного векселя?
8. Як розраховується ціна векселя?
9. Як визначається сума нарахованих відсотків і сума погашення банківського сертифікату?
10. Як розраховується ціна сертифікату?
ТЕСТИ
1. Ануїтет це:
1. Плата за використання грошових коштів
2. Ставка дисконтування
3. Постійні грошові платежі
4. Ряд рівних грошових виплат, які здійснюються через рівні проміжки часу
2. Терміновий ануїтет це:
1. Ануїтет, коли грошові виплати припадають на початок кожного періоду
2. Ануїтет, коли грошові виплати припадають на кінець кожного періоду
3. Ануїтет, на який нараховують прості відсотки
4. Ануїтет, на який нараховують складні відсотки
3. Майбутня вартість грошового потоку розраховується за формулою:
| 1. FV = PV*(1+i)n 2. PV = FV/(1+i)n 3. FV = PV*(1+i) 4. PV = FV/(1+i) | Де PV – теперішня вартість, FV – майбутня вартість, і – ставка дисконтування, n – кількість періодів. |
4. Теперішня вартість грошового потоку розраховується за формулою:
| 1. FV = PV*(1+i)n 2. PV = FV/(1+i)n 3. FV = PV*(1+i) 4. PV = FV/(1+i) | Де PV – теперішня вартість, FV – майбутня вартість, і – ставка дисконтування, n – кількість періодів. |
5.Майбутня вартість грошових коштів через n-періодів і при відомому значенні темпу їх приросту визначається за формулою:
1.FVn=PV(1+r)n
2.FVn=PV/(1+r)n
3. FVn=PV/(1+n)r
4. FVn=PV(1+n)n
6.Майбутня вартість грошових коштів через n-періодів m раз у рік і при відомому значенні темпу їх приросту визначається за формулою:
1.FVn=PV(1+rm)n
2.FVn=PV(1+r/m)nm
3. FVn=PV/(1+nm)rm
4. FVn=PV(1+rn)nm
7. Звичайний ануїтет це:
1. Ануїтет, коли грошові виплати припадають на початок кожного періоду
2. Ануїтет, коли грошові виплати припадають на кінець кожного періоду
3. Ануїтет, на який нараховують прості відсотки
4. Ануїтет, на який нараховують складні відсотки
8.Поточна вартість визначається за формулою:
1.PV=FVn/(1+rn)n
2. PV=FVn(1+r)n
3. PV=FVn/(n+r)n
4. PV=FVn/(1+r)n
9.Дисконтну ставку розраховуємо за формулою:
1.PV=FVn/(1+rn)n
2. PV=FVn/(1+r)n
3. PV=FVn/(n+r)n
4. PV=FVn(1+r)n
10.Ефективна ставка відсотку визначається:
1.EAR=(1+r/m)n-1
2.EAR=(1+r/m)m-1
3.EAR=(1+r/m)n-1
4.EAR=(1+r/m)nm-1
