|
Например, в предыдущей задаче мы установили, что f ''(2) = 0 и f ''(x) меняет знак при переходе через эту точку. Следовательно, х = 2 – точка перегиба графика функции f (x) =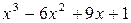 
.
Схема исследования функции и построение графика
Под «исследованием функции» понимают изучение её поведения (изменения) в зависимости от изменения аргумента. На основании исследования функции строят её график, предварительно изображая характерные точки.
Исследование функций и построение графиков можно проводить по следующей схеме:
1) найти область определения функции;
2) исследовать вопрос о чётности функции, о периодичности;
3) найти точки пересечения графика функции с осями координат;
4) изучить поведение функции при стремлении аргумента к концам промежутков области определения;
5) найти точки экстремумов, промежутки возрастания и убывания функции;
6) определить промежутки выпуклости функции, найти точки перегиба;
7) найти асимптоты графика функции.
Порядок исследования иногда целесообразно выбирать исходя из конкретных особенностей данной функции.
Пример 8.4. Исследовать функцию у =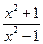 
и построить её график.
Вопросы для самоконтроля
1. Сформулируйте необходимый и достаточный признаки возрастания (убывания) функции в данной точке.
2. Дайте определения максимума и минимума функции.
3. Сформулируйте необходимое условие существования экстремума.
4. Какие значения аргумента (какие точки) называются критическими и как они находятся?
5. Сформулируйте достаточный признак существования экстремума.
6. Дайте определение выпуклости, вогнутости кривой.
7. Что называется точкой перегиба графика функции, как находятся эти точки?
8. Сформулируйте необходимый и достаточный признаки выпуклости и вогнутости кривой на заданном интервале.
9. Дайте определение асимптоты кривой. Как найти уравнения асимптот: вертикальных, горизонтальных, наклонных?
10. Изложите общую схему исследования функции и построение ее графика.
Литература
1. Письменный, Д. Т. Конспект лекций по высшей математике: в 2 ч. / Д. Т. Письменный. – М.: Айрис-пресс, 2004. – 280 с.
2. Кремер, Н. Ш. Высшая математика для экономистов / Н. Ш. Кремер. – М.: «Юнити». 1997 г. – 439 с.
3. Минорский, В. П. Сборник задач по высшей математике / В. П. Минорский. – М., 1978. – 352 с.
4. Яблонский, А. И. Высшая математика /А. И. Яблонский. – Мн.: Высшая школа, 2000. – 351 с.
5. Гусак, А. А. Задачи и упражнения по высшей математике / А. А. Гусак. – Мн.: Высшая школа, 1988. – 544 с.
6. Гурский, Е. И. Руководство к решению задач по высшей математике / Е. И. Гурский. – Мн.: Высшая школа, 1989. – 348 с.
7. Александров, П. С. Курс аналитической геометрии и линейной алгебры / П. С. Александров. – М.: Наука, 1979. – 512 с.
8. Сборник задач по алгебре и аналитической геометрии / А. А. Бурдун [и др.]. – Мн.: Университетское, 1999. – 302 с.
9. Милованов, М. В. Алгебра и аналитическая геометрия / М. В. Милованов, Р. И. Тышкевич, А. С. Феденко. – Мн.: Вышэйшая школа, 1984. – 269 с.
10. Гусак, А. А. Аналитическая геометрия и линейная алгебра: справочное пособие по решению задач / А. А. Гусак. – Мн.: ТетраСистемс, 2001. – 288 с.
11. Тер-Крикоров, А. М. Курс математического анализа: учебное пособие для вузов / А. М. Тер-Крикоров, М. И. Шабунин. – М.: Наука Гл. ред. физ.-мат. Лит., 2001. – 672 с.
12. Пискунов, Н. С. Дифференциальное и интегральное исчисления для вузов / Н. С. Пискунов. – М.: Наука, 1970. – 560 с.
13. Бугров, Я. С. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функция комплексного переменного / Я. С. Бугров, С. М. Никольский. – М.: Наука,1981. – 506 с.
14. Элементы линейной алгебры и аналитической геометрии / Р. Ф. Апатенок [и др.]. – Мн.: Вышэйшая школа, 1986. – 272 с.
15. Выготский, М. Я. Справочник по высшей математике / М. Я. Выготский. – М.: Наука, 1966. – 872 с.
16. Справочник по высшей математике / А. А. Гусак [и др.]. – Мн.: ТетраСистемс, 2000. – 638 с.
Производственно-практическое издание
БУЗЛАНОВ Александр Васильевич
БОРОДИЧ Елена Николаевна
БОРОДИЧ Руслан Викторович
БОРОДИЧ Тимур Викторович
Высшая математика:
