Определение 2.2. Число n называется размерностью линейного пространства V, если выполняются следующие условия:
1) в V существует n линейно независимых векторов;
2) любая система n + 1 векторов из V линейно зависима.
Размерность линейного пространства V обозначают dim V = n, то V называют n -мерным линейным пространством. Если пространство состоит из одного нулевого элемента, то его размерность считают равной нулю. Итак, размерность линейного пространства – это наибольшее возможное количество линейно независимых элементов в нём.
Базисом n -мерного линейного пространства V называется любая упорядоченная система n линейно независимых векторов этого пространства.
Примеры базисов линейных пространств:
1) базисом действительного пространства R 3 является любая тройка некомпланарных векторов. Базис действительного линейного пространства R 2 – любые два неколлинеарных вектора;
2) базисом n -мерного арифметического пространства Rn является, например, система векторов
е 1 = (1, 0, …, 0), е 2 = (0, 1, 0, …, 0), …, еn = (0, …, 0, 1).
Вопросы для самоконтроля
1. Что называют линейным пространством и каковы его свойства?
2. Приведите примеры линейного пространства.
3. Когда система векторов будет называться линейно независимой (линейно зависимой)?
4. Что называют размерностью линейного пространства?
5. Дайте определение базиса линейного пространства.
6. Приведите примеры базисов линейного пространства.
Предел функции
Математический анализ – раздел математики, в котором изучаются функции. Основу математического анализа составляет дифференциальное и интегральное исчисление, теория рядов. Заслуга открытия дифференциального исчисления принадлежит английскому математику и физику Исааку Ньютону (1643–1727) и Готфриду Вильгельму Лейбницу (1646–1716), немецкому математику и философу.
Понятие функции
Функция одной переменной
Понятие функции – одно из основных понятий современной математики.
Рассмотрим множество X элементов х и множество Y элементов y. Если каждому элементу х Î Χ поставлен в соответствие единственный элемент у Î Υ, обозначаемый у = f (x), то говорят, что на множестве Х задана функция у = f (x) со значениями во множестве Y. Элементы х Î Χ называются значениями аргумента, а элементы у Î Υ – значениями функции. Множество Х называется областью определения функции, множество всех значений функции – областью значений этой функции.
Употребляются следующие обозначения функции: у = f (x), y = F (x), y = Ф (х), у = φ(х) и т. п. Значение, которое функция у = f (x) принимает при х = а, обозначается f (a).
К традиционным основным способам задания функции относятся: аналитический, графический и табличный.
Аналитический способ задания функции – это задание функции с помощью формул. Например, у = 2 х, у = lg x, у = 
.
Функция заданная формулой у = f (x), правая часть которой не содержит у, называется явной функцией.
Рассмотрим уравнение F (x; y) = 0. Предположим, что существует непустое множество Х значений х таких, что при каждом х 0 Î Χ уравнение F (x 0; y) = 0 имеет действительные решения относительно у. Обозначим одно из них через у 0. Сопоставляя таким образом каждому х 0 Î Χ элемент у 0, получим функцию у = у (х), определённую на множестве Х и такую, что F (x; y (x)) º 0 для всех х Î Χ. Функция у = у (х), определённая таким образом, называется функцией, заданной неявно или неявной функцией.
Например, уравнение 3 х + 2 у – 5 = 0 неявно задаёт функцию у = −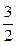 
х + 
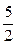. Уравнение х 2 + у 2 = R 2 задаёт неявно две функции у = 
и у = − .
Табличный способ задания функции – это способ задания функции при помощи таблицы. Примерами такого задания функции являются таблицы тригонометрических функций, таблицы логарифмов и т. д.
Графический способ задания функции – это способ задания функции при помощи графика. Графиком функции у = f (x) называется множество точек (x; f (x)) плоскости хОу, где х принадлежит области определения функции. Преимуществом графического способа задания функции является его наглядность.
Если у = f (u), u = φ(х) – функции своих аргументов, причём область определения функции у = f (u) содержит область значений функции u = φ(х), то каждому х из области определения функции φ соответствует такое у, что у = f (u), где u = φ(х). Эта функция, определяемая соответствием
y = f (φ(x))
называется сложной функцией или композицией функции φ и f. Например, если у = u 2, u = sin x, то у = sin2 x – сложная функция.
Кроме тригонометрических и обратных тригонометрических функций в средней школе изучаются функции: степенная у = ха (а = const), показательная у = ах (а = const), логарифмическая у = loga x (a = const). Все эти функции называются основными элементарными функциями. Элементарными функциями называются функции, которые можно получить из основных элементарных функций с помощью алгебраических действий и образования сложных функций. Например, функции у = lg sin x, y = x 2 + cos x, y = 3lgcos x + sin x являются элементарными.
