Пусть функция у = f (x) дифференцируема в некоторой окрестности точки х 0. Если в точке х = х 0 производная функции f (x) равна нулю и меняет знак при переходе через точку х 0, то точка х 0 является точкой экстремума, причём: 1) х 0 – точка максимума, если знак меняется с плюса на минус; 2) х 0 – точка минимума, если знак меняется с минуса на плюс.
Доказательство. Пусть в точке х 0 производная равна нулю и меняет знак с минуса на плюс, т. е. f '(x 0) = 0, f '(x) < 0 при х 0 − δ < x < x 0, f '(x) > 0 при х 0 < x < x 0 + δ (δ > 0). Тогда функция f (x) по теореме о достаточном условии возрастания и убывания функции убывает (х 0 − δ; х 0) и возрастает на интервале (х 0; х 0 + δ), т. е. f (x 0) < f (x) для всех х Î О (х 0, δ) = (х0 − δ; х 0 + δ), х ≠ х 0. Следовательно, х 0 – точка минимума.
Аналогично рассматривается случай, когда производная меняет знак с плюса на минус.
Достаточное условие экстремума можно выразить также с помощью второй производной.
Теорема 8.5. (достаточное условие экстремума).
Если в точке х = х 0 первая производная дифференцируема в некоторой окрестности точки х 0 функции у = f (x) равна нулю, а вторая производная отлична от нуля, то х 0 является точкой экстремума, причём: 1) х 0 – точка минимума, если f ''(x 0) > 0; 2) х 0 – точка максимума, если f ''(x 0) < 0.
Пример 8.2. Найти экстремумы функции f (x) =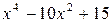 
.
Решение. Поскольку f '(x) =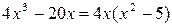 
, то критическими являются только стационарные точки 
, 
, 
.
Исследуем знак второй производной f ''(x) =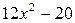 
в этих точках:
f ''(
) = 12 × 2 − 20 > 0, f ''(0) = −20 < 0, f ''(
) = 12 × 5 − 20 > 0.
Следовательно, 
, 
– точки минимума, – точка максимума, причём min f (x) = f () = f () = –10, max f (x) = f (0) = 15.
Интервалы выпуклости. Точки перегиба
Определение 8.8. График функции у = f (x) называется выпуклым вниз в данном промежутке, если он целиком расположен выше касательной в его произвольной точке (рисунок 8.7). График функции у = f (x) называется выпуклым вверх в данном промежутке, если он целиком расположен ниже касательной в его произвольной точке (рисунок 8.8).
|
|
Теорема 8.6. (достаточный признак выпуклости графика функции).
Если вторая производная функции у = f (x) положительна в данном промежутке, то график функции является выпуклым вниз в этом промежутке; если же вторая производная отрицательна в данном промежутке, то график функции является выпуклым вверх в этом промежутке.
Пример 8.3. Найти интервалы выпуклости графика функции f (x) = 
.
Решение. Найдём вторую производную функции f ''(x) = 
. Так как f ''(x) < 0 при х < 2 и f ''(x) > 0 при х > 2, то график функции является выпуклым вверх в интервале (−¥; 2) и выпуклым вниз – в интервале (2; +¥).
Определение 8.9. Точкой перегиба графика функции у = f (x) называется такая его точка М 0 (рисунок 8.9), в которой меняется направление выпуклости.
