Теорема 4.1. Функция у = у (х) не может иметь более одного предела при х → 
.
Доказательство. Предположим противное, пусть функция у = у (х) при х → имеет два предела А 1 ≠ А 2. По свойствам бесконечно малых функций (б.м.ф.) у (х) = А 1 + a1(х) и у (х) = А 2 + a2(х), где a1(х), a2(х) – б.м.ф. при х → . Тогда А 1 + a1(х) = А 2 + a2(х) или А 1 – А 2 = a1(х) – a2(х). Но последнее равенство невозможно, т. к. в левой части стоит постоянная, отличная от нуля, а в правой – бесконечно малая функция.
Теорема 4.2. Если каждая из функций у = у (х), z = z (x) имеет предел при х → , то сумма, разность, произведение этих функций также имеют пределы, причём
1) 
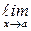(у (х) ± z (x)) = 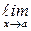y (x) ± 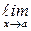z (x);
2) 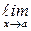(y (x) × z (x)) = 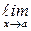y (x) × 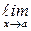z (x),
если кроме того, 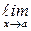z (x) ≠ 0, то частное 
имеет предел, причём
3) 
= 
.
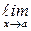
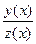Доказательство. Пусть 
y (x) = А, z (x) = В.
Тогда по свойствам б.м.ф. у (х) = А + a(х), z (x) = B + b(x), где a(х), b(х) – б.м.ф. при х → . Получаем:
1) у (х) ± z (x) = (А ± В) + (a(х) ± b(х)). По свойствам б.м.ф. a(х) ± b(х) – б.м.ф., поэтому 
(у (х) ± z (x)) = А ± В, т. е. (у (х) ± z (x)) = y (x) ± z (x);
2) y (x) × z (x) = (А + B + b(x) = А × В + a(х) × B + А × b(x) + a(х) × b(x). По свойствам б.м.ф. функция a(х) × B + А × b(x) + a(х) × b(x) – б.м.ф. при х → 
.
Поэтому (y (x) × z (x)) = АВ = y (x) × z (x);
3) Пусть В ≠ 0. Рассмотрим разность
− 
.
По свойствам б.м.ф. функция 
– б.м.ф. при х → .
Рассмотрим функцию 
= .
Очевидно, что = 
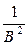. Это означает, что для e, равного, например, 
найдутся х, расположенные вокруг точки такие, что │ − 
│< , т. е. − < − < , < < 
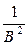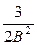. Но это означает, что функция ограничена. Тогда по свойствам б.м.ф. произведение
– б.м.ф. при х → .
Обозначим её a1(х), т. е. 
= a1(х). Тогда 
+ a1(х). По свойствам б.м.ф. = 
= .
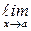
Следствие 4.1. Постоянный множитель можно выносить за знак предела, т. е. если с = const, то (с × у (х)) = с у (х).
Следствие 4.2. Если у (х) = А, то для любого натурального числа m 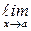(у (х)) m = ( 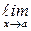у (х)) m = Am.
Теорема 4.3. Пусть три функции u = u (x), v = v (x), y = y (x) определены в некотором промежутке, содержащем точку . Если для любого х из этого промежутка выполняется неравенства u (x) £ y (x) £ v (x) и функции u = u (x), v = v (x) имеют одинаковые пределы при х → , то функция у = у (х) имеет тот же предел при х → .
Доказательство. Пусть 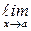u (x) = 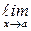v (x) = A. Т. к. u (x) £ y (x) £ v (x), то u (x) − А £ y (x) − А £ v (x) − А.
По определению предела функции "e > 0 существуют d1 > 0 и d2 > 0 такие, что из неравенств 0 <│ х − │< d1 следует │ u (x) − A │< e, а из неравенств 0 <│ х − 
│< d2 следует │ v (x) − A │< e. Обозначим d = min{d1, d2}. Тогда для х, удовлетворяющих неравенствам 0 <│ х − │< d следует −e < u (x) − A < e и −e < v (x) − A < e. Поэтому из неравенств u (x) − А £ y (x) − А £ v (x) − А следует −e < у (x) − A < e, т. е. │ у (x) − A │< e. Это означает, что 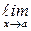у (х) = А.
Теорема 4.4. Пусть функция у = f (x) определена в некотором промежутке, содержащем точку . Если при х → функция у = f (x) имеет положительный (отрицательный) предел, то найдётся такой промежуток вокруг точки , что для всех х из этого промежутка функция положительна (отрицательна).
Доказательство. Пусть 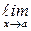f (x) = А. Это означает, что "e > 0 можно указать такое число d > 0, что при всех х, удовлетворяющих условию 0 <│ х − │< d, выполняется неравенство │ f (x) − A │< e, т. е. −e < f (x) − A < e.
Если А > 0, то взяв e = 
А из неравенства A − e < f (x), получим f (x) > A − e = = A − A = A > 0, т. е. f (x) > 0 при −d < x − < d, т. е. при − d < x < d + .
Если А < 0, то взяв e = − А, из неравенства f (x) < A + e получим f (x) < A + e = = A − A = A < 0, т. е. f (x) < 0 при − d < x < d + .
Эта теорема называется теоремой о сохранении знака функции, имеющей предел.
Теорема 4.5. Если функции u (x), v (x) определены в некотором промежутке, содержащем точку , и для всех х из этого промежутка, кроме х = , выполняется неравенство u (x) < v (x), причём функции u (x) и v (x) имеют пределы при х → . Тогда u (x) £ 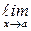v (x).
Доказательство. Пусть 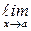u (x) = А, 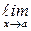v (x) = В. Положим, что А > B. По теореме 4.2 
(u (x) − v (x)) = А – В > 0. По теореме 4.4 найдётся промежуток вокруг точки такой, что для всех х из этого промежутка u (x) − v (x) > 0, т. е. u (x) > v (x), что противоречит условию.
Следовательно, предположение неверно и А £ В, т. е. 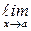u (x) £ 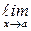v (x).
Замечательные пределы
Определение 4.1. Будем говорить, что отношение двух функций f (x)/ g (x) есть неопределённость вида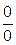 
(или 
) при х → , если числитель и знаменатель дроби – бесконечно малые функции (бесконечно большие функции) при х → . В этом случае о пределе отношения f (x)/ g (x) при х → ничего определённого сказать нельзя: он может быть равен нулю, бесконечности, числу, отличному от нуля, а может и вовсе не существовать. Раскрыть эти неопределённости – значит вычислить предел отношения f (x)/ g (x), если он существует, или доказать, что он не существует. Для раскрытия неопределённостей применяют различные методы.
