Пусть даны две прямые  и
и 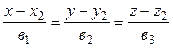 .
.
Очевидно, что прямые лежат в одной плоскости тогда и только тогда, когда векторы  ,
, 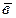 и
и  компланарны, т. е.
компланарны, т. е.
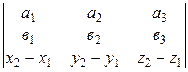 = 0. (1.9)
= 0. (1.9)
Если в (1.9) первые две строки пропорциональны, то прямые параллельны. Если все три строки пропорциональны, то прямые совпадают. Если условие (1.9) выполнено и первые две строки не пропорциональны, то прямые пересекаются.
Если же 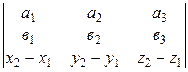 ¹ 0, то прямые являются скрещивающимися.
¹ 0, то прямые являются скрещивающимися.
Задачи на прямую и плоскость в пространстве
Прямая, как пересечение двух плоскостей
Пусть заданы две плоскости
А 1х + В 1у + С 1 z + D 1 = 0,
А 2 х + В 2 у + С 2 z + D 2 = 0.
Если плоскости не являются параллельными, то нарушается условие
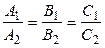 .
.
Пусть, например  ¹
¹ 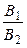 . Найдём уравнение прямой, по которой пересекаются плоскости. В качестве направляющего вектора искомой прямой можно взять вектор
. Найдём уравнение прямой, по которой пересекаются плоскости. В качестве направляющего вектора искомой прямой можно взять вектор
 =
=  ×
×  =
= 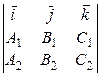 =
=  .
.
Чтобы найти точку, принадлежащую искомой прямой, фиксируем некоторое значение z = z 0 и решая систему
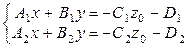 ,
,
получаем значения х = х 0, у = у 0. Итак, искомая точка М (х 0; у 0; z 0).
Искомое уравнение
 .
.
Взаимное расположение прямой и плоскости
Пусть задана прямая  ,
,  ,
, 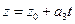
 и плоскость А 1 х + В 1 у + С 1 z + D 1 = 0. Чтобы найти общие точки прямой и плоскости, необходимо решить систему их уравнений
и плоскость А 1 х + В 1 у + С 1 z + D 1 = 0. Чтобы найти общие точки прямой и плоскости, необходимо решить систему их уравнений

откуда А 1( ) + B 1(
) + B 1( ) + C 1(
) + C 1( ) + D 1 = 0,
) + D 1 = 0,
(A 1  1 + B 1
1 + B 1  2 + C 1
2 + C 1  3) t + (A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1) = 0.
3) t + (A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1) = 0.
Если А 1 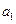 + В 1
+ В 1 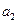 + С 1
+ С 1  ¹ 0, то система имеет единственное решение
¹ 0, то система имеет единственное решение
t = t 0 = – 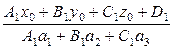 .
.
В этом случае прямая и плоскость пересекаются в единственной точке М 1(х 1; у 1; z 1), где  ,
,  ,
, 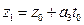 .
.
Если A 1  1 + B 1
1 + B 1  2 + C 1
2 + C 1  3 = 0, А 1 x 0 + В 1 y 0 + С 1 z 0 + D 1 ¹ 0, то прямая и плоскость не имеют общих точек, т. е. параллельны.
3 = 0, А 1 x 0 + В 1 y 0 + С 1 z 0 + D 1 ¹ 0, то прямая и плоскость не имеют общих точек, т. е. параллельны.
Если же A1  1 + B1
1 + B1  2 + C1
2 + C1  3 = 0, А 1 x 0 + В 1 y 0 + С 1 z 0 + D 1 = 0, то прямая принадлежит плоскости.
3 = 0, А 1 x 0 + В 1 y 0 + С 1 z 0 + D 1 = 0, то прямая принадлежит плоскости.
Угол между прямой и плоскостью
Найдём угол j между прямой  =
=  =
=  и плоскостью А 1 х + В 1 у + С 1 z + D 1 = 0.
и плоскостью А 1 х + В 1 у + С 1 z + D 1 = 0.
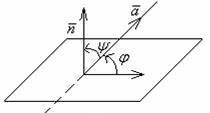 Поскольку вектор
Поскольку вектор  = (А 1; В 1; С 1) образует с направляющим вектором
= (А 1; В 1; С 1) образует с направляющим вектором  =
= 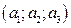 угол y =
угол y = 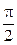 – j или y =
– j или y = 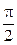 + j (рисунки 1.3 и 1.4), то
+ j (рисунки 1.3 и 1.4), то

|
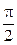 – j) или cosy = cos(
– j) или cosy = cos(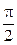 + j), откуда cosy = sinj или cosy = – sinj.
+ j), откуда cosy = sinj или cosy = – sinj.
|
sinj =ôcosyô= 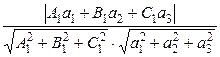 .
.
Расстояние от точки до плоскости
Пусть плоскость задана общим уравнением Ах +Ву + Сz +D = 0. Расстояние от точки М (х 0; у 0; z 0) до данной плоскости вычисляется по формуле
d = 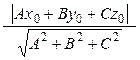 .
.
Поверхности второго порядка
Цилиндры второго порядка
Определение 1.3. Цилиндрической поверхностью называется поверхность, описываемая прямой (образующей), движущейся вдоль некоторой линии (направляющей) и остающейся параллельной исходному направлению.
Определение 1.4. Цилиндром второго порядка называется цилиндрическая поверхность, направляющей которой является эллипс (окружность), гипербола или парабола.
Рассмотрим цилиндры второго порядка, у которых образующая параллельна оси Оz (рисунки 1.5, 1.6, 1.7).
1) Эллиптический
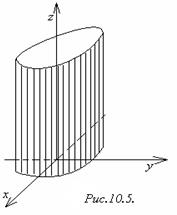 цилиндр цилиндр
В частности эллиптический цилиндр имеет в качестве направляющей окружность. Его уравнение | 2) Гиперболический
цилиндр

 – – 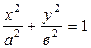
| 3) Параболический
цилиндр
х 2 = 2 ру |






 или
или 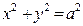 .
.
