Пусть даны три точки пространства М 1(х 1; у 1; z 1), М 2(х 2; у 2; z 2), M 3(x 3; y 3; z 3), не лежащие на одной прямой. Пусть М (х; у; z) – произвольная точка этой плоскости 
(х – х 0; у – у 0; z – z 0), 
(х 2 – х 1; у 2 – у 1; z 2 – z 1), (х 3 – х 1; у 3 – у 1; z 3 – z 1) компланарны. Поэтому их смешанное произведение равно нулю:
= 0.
Следовательно, искомое уравнение
= 0. (1.3)
Взаимное расположение двух плоскостей
Пусть даны две плоскости
А 1 х + В 1 у + С 1 z + D 1 = 0,
А 2 х + В 2 у + С 2 z + D 2 = 0.
Первая плоскость имеет нормальный вектор 
(А 1; В 1; С 1), вторая плоскость 
(А 2; В 2; С 2).
Если плоскости параллельны, то векторы и коллинеарны, т. е. = l для некоторого числа l. Поэтому
– условие параллельности плоскости.
Условие совпадения плоскостей:
,
так как в этом случае умножая второе уравнение на l = 
, получим первое уравнение.
Если условие параллельности не выполняется, то плоскости пересекаются. В частности, если плоскости перпендикулярны, то перпендикулярны и векторы 
, 
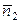. Поэтому их скалярное произведение равно 0, т. е.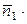 
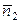= 0 или
А 1 А 2 + В 1 В 2 + С 1 С 2 = 0.
Это необходимое и достаточное условие перпендикулярности плоскостей.
Угол между двумя плоскостями
Угол между двумя плоскостями
А 1 х + В 1 у + С 1 z + D 1 = 0,
А 2х + В 2 у + С 2 z + D 2 = 0
– это угол между их нормальными векторами и , поэтому
cosj = 
= 
.
Прямая в пространстве
Векторно-параметрическое уравнение прямой
Определение 1.2. Направляющим вектором прямой называется любой вектор, лежащий на прямой или параллельный ей.
|
Составим уравнение прямой, проходящей через точку М 0(х 0; у 0; z 0) и имеющей направляющий вектор 
= 
(рисунок 1.2). Отложим из точки М 0 вектор 
. Пусть М (х; у; z) – произвольная точка данной прямой, а 
– её радиус-вектор точки М 0. Тогда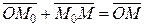 
, 
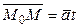, поэтому 
. Это уравнение называется векторно-параметрическим уравнением прямой.Параметрические уравнения прямой
В векторно-параметрическом уравнении прямой 
перейдёт к координатным соотношениям (х; у; z) = (х0; у0; z0) + 
t. Отсюда получаем параметрические уравнения прямой
,
, (1.4)
.
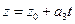Канонические уравнения прямой
Из уравнений (1.4) выразим t: 
t = 
, t = 
, t = 
,
откуда получаем канонические уравнения прямой
= 
= 
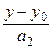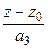. (1.5)
Уравнение прямой, проходящей через две данные точки
Пусть даны две точки М 1(х 1; у 1; z 1) и М 2(х 2; у 2; z 2). В качестве направляющего вектора прямой можно взять вектор = 
(х 2 – х 1; у 2 – у 1; z 2 – z 1). Поскольку прямая проходит через точку М 1(х 1; у 1; z 1), то её канонические уравнения в соответствии с (1.5) запишутся в виде
. (1.6)
Угол между двумя прямыми
Рассмотрим две прямые с направляющими векторами = и 
. Угол между прямыми равен углу между их направляющими векторами, поэтому
сosj = 
= 
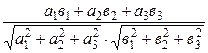. (1.7)
Условие перпендикулярности прямых:
.
Условие параллельности прямых:
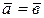l,
т. е.
. (1.8)
