Определение 1.5. Поверхностью вращения второго порядка называется поверхность, образованная вращением линии второго порядка вокруг её оси (рисунки 1.8–1.12).
1) Эллипсоид вращения


При вращении эллипса | 2) Однополостный гиперболоид
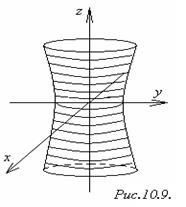
Однополостный гиперболоидобразуется при вращении гиперболы | ||||||||||||||
3) Двуполостный
гиперболоид
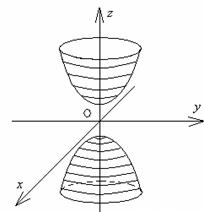
Двуполостный гиперболоидобразуется при вращении гиперболы | 4) Конус вращения

Конус вращенияобразуется при вращении прямых | 5) Параболоид
вращения

х 2 + у 2 = 2 рz или
Параболоид вращенияполучается вра-щением параболы у 2 = 2 рz, х = 0 вокруг оси Оz | |||||||||||||
Поверхности второго порядка
 |
1. Трёхосный эллипсоид
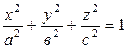 (рисунок 1.13).
(рисунок 1.13).
|
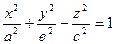 .
.
3. Двуполостный гиперболоид  .
.
4. Конус второго порядка 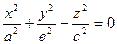 .
.
5. Эллиптический параболоид  .
.
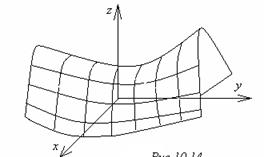 |
6. Гиперболический параболоид
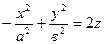 (рисунок 1.14).
(рисунок 1.14).
|
Вопросы для самоконтроля
1. Как проверить, лежит ли данная точка на поверхности, заданной уравнением?
2. Всегда ли два уравнения с тремя переменными определяют некоторую линию в пространстве? Приведите примеры.
3. Какое множество точек представляет собой уравнение с двумя переменными, если его рассматривать в пространстве?
4. При каких условиях общее уравнение второй степени с тремя переменными определяет сферу? Как найти ее центр и радиус?
5. Как записать уравнение поверхности вращения, полученной при вращении плоской линии f(x, y) = 0 вокруг оси Ox? Приведите примеры.
6. Каков характерный признак, отличающий уравнение плоскости в декартовых координатах от уравнения других поверхностей?
7. Как будет располагаться плоскость относительно осей координат, если в ее уравнении отсутствуют те или иные члены?
8. Как определить направляющий вектор прямой, если она задана общим уравнением?
9. Как определяется угол между двумя плоскостями, между двумя прямыми, между прямой и плоскостью?
10. Каковы условия перпендикулярности и параллельности двух плоскостей, двух прямых, прямой и плоскости?
11. Как найти точку пересечения прямой и плоскости?
12. При каких условиях данная прямая лежит в данной плоскости?
13. Как найти расстояние от точки до плоскости?
14. Напишите виды и уравнения цилиндров второго порядка.
15. Напишите виды и уравнения поверхностей вращения второго порядка.
16. Напишите виды и уравнения поверхностей второго порядка.
Линейные пространства





 , х = 0 вокруг оси Оz получим поверхность, которая называется эллипсоидом вращения. При а = с получаем сферу х 2 + у 2 + z 2 = a 2.
, х = 0 вокруг оси Оz получим поверхность, которая называется эллипсоидом вращения. При а = с получаем сферу х 2 + у 2 + z 2 = a 2.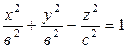
 , х = 0 вокруг оси Оz.
, х = 0 вокруг оси Оz.
 , х = 0 вокруг оси Оz.
, х = 0 вокруг оси Оz.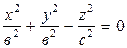
 , х = 0 вокруг оси Оz.
, х = 0 вокруг оси Оz.


