Упорядоченная тройка некомпланарных векторов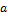 
, 
, 
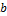в трёхмерном пространстве называется правой, если с конца вектора кратчайший поворот от вектора 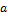к вектору 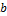виден наблюдателю против часовой стрелки. И наоборот, если кратчайший поворот виден по часовой стрелке, то тройка называется левой.
104. Дать определение векторного произведения геометрических векторов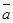 
и 
.
Векторное произведение двух векторов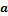 
и 
- называется третий вектор , обозначаемый 
, при этом:
1) Вектор c ортогонален каждому из векторов 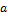и ;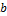
2) Если векторы 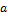, , 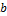отложены от одной точки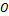 
, то эта тройка будет правой;
, где 
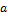– угол между векторами и 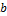. Если векторы 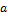и 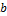параллельны, то полагается 
;
Свойства векторного произведения.
1) 
2) 
;
3) 
;
4) Величина 
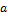равна площади параллелограмма, построенного на векторах и ;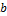
5) Если векторы 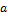и 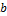заданы в правой декартовой системе координат (поворот от вектора 
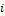к вектору 
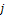на угол 
с конца вектора 
виден, совершающимся против часовой стрелки), то
,
где 
, 
.
106. Геометрический смысл |[ , ]|.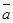
1) Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулю их векторного произведения;
2) Модуль векторного произведения равняется площади 
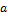параллелограмма, построенного на приведённых к общему началу векторах и ;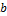
3) Если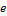 
— единичный вектор, ортогональный векторам 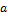и 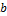и выбранный так, что тройка 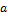, , 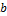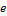— правая, а — площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:
4) Если — какой-нибудь вектор, 
— любая плоскость, содержащая этот вектор, 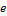— единичный вектор, лежащий в плоскости и ортогональный к , 
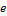— единичный вектор, ортогональный к плоскости и направленный так, что тройка векторов , , является правой, то для любого лежащего в плоскости вектора 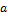справедлива формула:
.
Формула вычисления векторного произведения, если известны декартовы координаты векторов.
,
где , .
108. Дать определения смешанного произведения трёх векторов.
Смешанное произведение трёх векторов , ,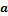 
– скалярное произведение векторного произведения первых двух на третий:
.
109. Геометрический смысл |( , ,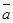 
)| и знака ( , , ).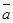
С помощью смешанного произведения можно вычислить объём параллелепипеда, построенного на трёх векторах:
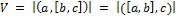
Если смешанное произведение больше нуля, то тройка правая, иначе – левая.
110. Как узнать компланарна тройка векторов 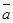, , или нет, используя понятие смешанного произведения?
Тройка векторов компланарна тогда и только тогда, когда их смешанное произведение равно нулю.
