Можно использовать два метода: звёздочкой и разложением по 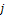 -той (-тому) строке (столбцу). Приведу пример последнего. Тогда определитель будем равен сумме:
-той (-тому) строке (столбцу). Приведу пример последнего. Тогда определитель будем равен сумме: 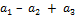 , где
, где 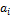 – произведение
– произведение 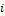 -того элемента
-того элемента 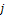 -той строки/
-той строки/ 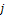 -того столбца на определитель минора
-того столбца на определитель минора 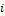 -того элемента
-того элемента 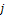 -той строки/
-той строки/ 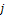 -того столбца.
-того столбца.
15. Как изменится определитель при транспонировании матрицы?
Никак, поскольку элементы и количество инверсий от транспонирования не поменяются.
16. Чему равен определитель, имеющий стоку или столбец, целиком состоящий из нулей?
Определитель такой матрицы будет равен нулю, т.к. при разложении по этой строке/столбцу будет сумма произведений нулей на миноры.
17. Как изменится определитель, если его строку или столбец умножить на число α?
Определитель станет больше в α раз.
18. Как изменится определитель, если в нем переставить две строки или два столбца?
Он умножится на  .
.
Опишите, в чем заключается линейное свойство определителя.
Если в определителе 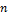 -го порядка
-го порядка 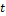 некоторая строка
некоторая строка 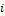
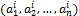 является линейной комбинацией двух строк
является линейной комбинацией двух строк 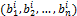 и
и 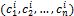 с коэффициентами
с коэффициентами 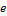 и
и 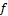 , то
, то 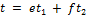 , где
, где 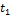 – определитель, у которого
– определитель, у которого 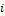 -тая строка равна
-тая строка равна 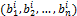 , а все остальные – те же, что и у
, а все остальные – те же, что и у 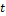 , а
, а 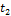 – определитель, у которого
– определитель, у которого 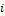 -тая строка равна
-тая строка равна 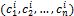 , а все остальные – те же, что и у
, а все остальные – те же, что и у 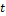 .
.
20. Как изменится определитель, если к какой-либо его строке прибавить другую, умноженную на некоторое число?
Никак не изменится.
21. Как изменится определитель, если к какой-либо строке, умноженной на число α, добавить другую строку, умноженную на число β?
В таком случае определитель будет умножен на число 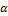 .
.
22. Чему равен определитель, имеющий две пропорциональные строки?
Он равен нулю.
23. Как связаны между собой определители матриц А и λА?
Пусть  и
и  , где
, где 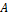 – матрица размера
– матрица размера 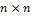 , тогда
, тогда
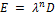 .
.
24. Чему равен определитель произведения матриц А и В?
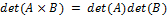 .
.
25. Дайте определение алгебраического дополнения 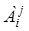 элемента
элемента 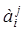 .
.
Алгебраическое дополнение 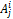 элемента
элемента 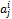 – произведение минора данного элемента на
– произведение минора данного элемента на 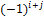 .
.
Сформулируйте две теоремы об алгебраических дополнениях.
1) Сумма произведений элементов какой-либо строки (или столбца) определителя на их алгебраические дополнения равна определителю.
2) Сумма произведений всех элементов строки (столбца) на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю.
27. Дайте определение минора  .
.
Минор элемента 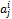 – определитель матрицы, составленной из элементов исходной матрицы за исключением элементов строки
– определитель матрицы, составленной из элементов исходной матрицы за исключением элементов строки 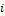 и столбца
и столбца 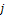 .
.
Сформулируйте теорему о связи минора и алгебраического дополнения.
Алгебраическое дополнение 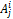 и минор
и минор 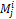 связаны соотношением
связаны соотношением 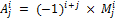 .
.






