Пусть даны две прямые:
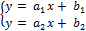
или
Тогда угол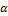 
находится по формуле:
или
157. Как охарактеризовать взаимное расположение двух прямых А1х+В1у+С1=0, А2х+В2у+С2=0?
Первое, что нужно сделать – проверить на параллельность. В этом случае угол между ними будет равен нулю. Если же угол нулю не равен, то нужно определить, в одной или в разных плоскостях они находятся. В первом случае они будут пересекаться, во втором – скрещиваться. Для определения этого пункта необходимо найти расстояние между этими прямыми: если нуль, то в одной плоскости.
Уравнения этих прямых также можно записать в виде:
и 
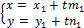или
и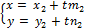 
где
Теперь можно запросто найти расстояние между двумя прямыми:
158. Запишите в векторной и координатной форме уравнения плоскости, проходящей через точку М0(х0,у0,z0) перпендикулярно вектору 
={А,В,С}.
У точки 
есть радиус-вектор 
.
1) Векторная форма уравнения плоскости:
,
где 
– радиус-вектор произвольной точки на плоскости.
2) Координатная форма уравнения плоскости:
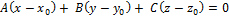
Запишите общее уравнение плоскости. Охарактеризуйте его коэффициенты.
Общее уравнения плоскости:
,
где 
.
160. Запишите в векторной и координатной форме уравнения плоскости, проходящей через точку М0(х0,у0,z0) с радиусом вектором 
параллельно векторам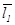 
={m1,n1,p1} и 
={m2,n2,p2}.
Можно положить 
, тогда уравнение плоскости в векторной форме:
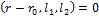
и в координатной форме:
161. Запишите формулу вычисления расстояния от точки М0(х0,у0,z0) до плоскости Ах+Ву+Сz+D=0.
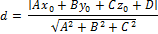
162. Как найти угол между двумя плоскостями А1х+В1у+С1z+D1=0 и А2х+В2у+С2z+D2=0?
163. Как охарактеризовать взаимное расположение трёх плоскостей по заданным общим уравнениям?
Пусть имеется три плоскости, заданные уравнениями:
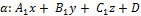
При этом им соответствуют их нормальные векторы:
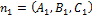
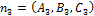
Далее рассмотрим различные случаи:
1) Если смешанное произведение трёх нормальных векторов не равно нулю, то все три плоскости пересекаются в одной точке, координаты которой можно найти, решив систему:
2) Если смешанное произведение нормальных векторов равно нулю, и при этом система не имеет решений, то возможен один из следующих вариантов:
a) две плоскости совпадают, а третья параллельна им;
b) все три плоскости параллельны друг другу;
c) две плоскости параллельны, а третья пересекает их;
d) каждая пара плоскостей пересекается, при этом все три вектора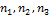 
лежат в одной плоскости.
3) Если смешанное произведение нормальных векторов равно нулю, и при этом система имеет бесконечное множество решений, то возможен один из следующих вариантов:
a) все три плоскости совпадают;
b) две плоскости совпадают, а третья пересекает их;
c) все три плоскости пересекаются по одной прямой, но все три вектора 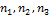лежат в одной плоскости.
