1) Однородная система линейных уравнений имеет нетривиальные решения тогда и только тогда, когда ранг её матрицы меньше числа неизвестных.
2) Однородная система линейных уравнений в случае, когда ранг её матрицы равен числу неизвестных, имеет нетривиальные решения тогда и только тогда, когда определитель её матрицы равен нулю.
79. Свойства решений системы линейных однородных уравнений.
1) Сумма любых двух частных решений однородной системы линейных уравнений является решением этой системы.
2) Произведение любого частного решения однородной системы линейных уравнений на любое число является решением этой системы.
80. Из каких свойств решений линейной однородной системы следует, что множество всех решений таких систем образует линейное пространство? Какова его размерность?
Размерность такого пространства равна разности размерности количества неизвестных и ранга матрицы системы.
81. Дайте определение фундаментальной системы решений однородной системы линейных уравнений. Сколько решений содержит Ф.С.Р.?
Фундаментальная система решений – базис подпространства, образуемого множеством всех решений системы. Она содержит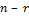 
решений, где 
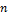– количество неизвестных, а 
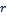– ранг матрицы.
82. Дайте определение геометрического вектора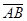 
, его модуля | 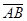| и нулевого вектора. Какие два вектора называются коллинеарными?
Геометрический вектор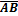 
– упорядоченная пара точек 
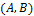, где 
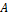– начало вектора, а 
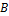– конец вектора. Также вектор можно трактовать как направленный отрезок.
Модуль вектора – расстояние между начало и концом вектора.
Коллинеарные векторы – векторы, лежащие на одной прямой или параллельных прямых.
83. Какие два вектора 
и 
называются равными?
Два вектора называются равными, если коллинеарные и одинаково ориентированные, при этом у них одинаковая длина (равные модули).
84. Как отложить вектор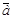 
от точки А?
Для этого нужно построить вектор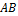 
, равный 
.
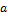85. Как определяется операция сложения векторов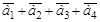 
?
Суммой векторов является вектор, координаты которого являются суммой соответствующих координат суммируемых векторов.
86. Как определяется операция умножения вектора на число?
Произведением вектора 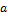на число 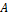называется вектор 
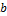, обозначаемый 
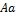, и определяемый условиями:
1) 
, если 
;
2) 
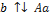, если 
;
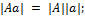
4) 
.
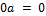87. Дать определение понятий: «Линейная комбинация геометрических векторов», «Линейно зависимые и линейно независимые системы векторов».
Линейная комбинация геометрических векторов – вектор, образуемый суммой нескольких векторов с различными коэффициентами.
Линейно зависимая система векторов – система векторов, где векторы являются линейной комбинацией друг друга.
Линейно независимая система векторов – система векторов, где ни один вектор не является линейной комбинацией других.
88. Понятие аффинного и декартова базиса во множестве геометрических векторов. Понятие координат вектора. Как устроен базис на прямой, плоскости и в пространстве?
Аффинная система координат – конструкция, состоящая из точки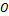 
и приложенного к ней векторного базиса.
Декартовый базис – базис, у которого все векторы попарно ортогональны и единичны.
Декартова система координат – конструкция, состоящая из произвольной точки 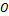и приложенного к ней декартова базиса.
Координаты вектора – коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.
Базис – это набор линейно независимых векторов, через которые можно выразить любой другой вектор. В зависимости от того, где определяется базис, может быть разное количество этих векторов с разным количеством координат: один на прямой с одной координатой, два на плоскости с двумя координатами и три в пространстве с тремя координатами.
89. Что означает геометрически линейная зависимость системы двух векторов?
В случае, когда два вектора линейно зависимы, они коллинеарны.
90. Какая система векторов называется компланарной? Что означает геометрически линейная зависимость системы из трёх и более векторов?
Система векторов называется компланарной, когда имеется некая плоскость, которой каждый из векторов системы параллелен. Если такой плоскости нет, то эта система векторов линейно зависима.
91. Понятие аффинной и декартовой систем координат. Как называют оси в декартовой системе координат?
Аффинная система координат – конструкция, состоящая из точки 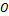и приложенного к ней векторного базиса.
Декартова система координат – конструкция, состоящая из произвольной точки 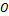и приложенного к ней декартова базиса.
В декартовой системе координат оси называются так: абсцисса, ордината, аппликата.
92. Понятие радиуса-вектора точки и координат точки. Как найти координаты вектора, зная координаты его конца и начала?
Радиус-вектор – вектор, идущий в точку пространства из какой-либо заранее фиксированной точки (обычно начала координат).
Координаты точки – совокупность чисел, определяющих положение этой точки.
Чтобы найти координаты вектора, нужно вычесть из координат конца координаты начала.
93. Как понимаете утверждение: «Точка М делит отрезок АВ в отношении λ.
Это значит, что следующее равенство верно:
94. Запишите координаты точки М, делящей отрезок АВ в отношении λ, если А(х1,у1), В(х2,у2).
Пусть координаты точки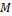 
– 
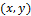, тогда:
и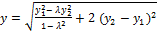 
,
если использовать модуль координат векторов, иначе так:
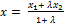и 
.
95. Понятие проекции точки на ось и проекции вектора на ось. Чему равна проекция вектора 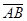на ось 
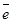, если ( 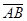^ 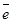)= φ?
Проекция точки на ось – основание перпендикуляра, опущенного из данной точки на ось.
Скалярная проекция вектора на ось – это число, абсолютная величина которого равна длине отрезка оси, заключённого между проекциями точки начала и точки конца вектора:
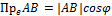
96. Дайте определение скалярного произведения геометрических векторов. Его свойства.
Скалярное произведение векторов – число, равное произведению их модулей на косинус угла между ними:
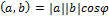
Его свойства:
1) 
;
2) 
;
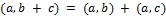3) 
;
.
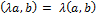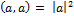97. Как узнать, используя скалярное произведение, какой угол (прямой, тупой или острый) образуют векторы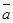 
и 
?
Через косинус угла между векторами:
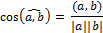
Если косинус положительный, то угол острый; если косинус равен нулю, то угол прямой; если косинус отрицательный, то угол тупой.
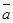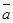98. Запишите формулы вычисления скалярного произведения ( , ) если известны декартовы координаты векторов и ?
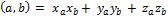
99. Как, используя понятие скалярного произведения, найти длину вектора и расстояние между двумя точками?
1) Длина вектора a:
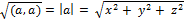
2) Расстояние d между точками A и B:
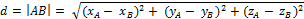
100. Как найти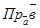 
, cos ( ^ )?
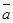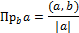
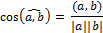
101. Дайте определение направляющих косинусов вектора. Как их найти?
Направляющий косинус – косинус угла между вектором и осью координат.
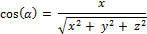
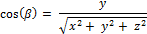
102. Понятие орта вектора. Как найти координаты орта вектора?
Орт вектора – вектор, направленный так же, как и исходный вектор, но имеющий длину, равную единице. Его координаты совпадают с его направляющими косинусами.
