Система с ограниченной очередью (конечным накопителем).
Система с потерями (отказами).
Многолинейная система с общей очередью (с общим накопителем).
Система с ограниченным временем ожидания.
Приоритетные системы (системы с приоритетным обслуживанием).
Примеры применения методов теории массового обслуживания в экономике.
Оптимизация норм обслуживания и норм численности рабочих при многостаночном обслуживании
Оценка целесообразности овладения смежными профессиями
Определение оптимального количества кладовщиков на складе (по А.А.Воронову).
Выбор оптимального варианта структуры управления.
Оптимизация организационных форм и дисциплины обслуживания.
Выбор оптимальной организационной формы технического обслуживания.
Выбор оптимальной дисциплины технологического обслуживания.
Основные понятия и определения ТМО (СМО)
Дадим определение основным понятиям теории массового обслуживания.
В терминах СМО одиночный входной сигнал называют требованием (заявкой), а временную последовательность однотипных одиночных сигналов - входным потоком требований (заявок).
Продолжительность преобразований одиночного входного сигнала называют временем обслуживания одного требования.
СМО могут быть одноканальными и многоканальными. Одноканальная система обслуживает одновременно только одно требование, многоканальная - несколько требований.
Если к моменту поступления очередного требования цикл обслуживания предыдущего не закончился, то вновь поступившее требование или теряется и в дальнейшем процессе не участвует, или ожидает окончания цикла, после чего начинается его обслуживание.
В первом случае система называется системой обслуживания с потерями (отказами), во втором - системой обслуживания с ожиданием.
В многоканальной системе с ожиданием требование, поступившее в момент, когда все каналы системы заняты, становится в очередь и ждет, пока не освободится один из каналов. При этом обслуживание требования в очереди может иметь определенный порядок или быть случайным. Время ожидания в очереди может быть как ограниченным, так и неограниченным.
Для СМО с потерями одной из наиболее важных характеристик является вероятность отказа в обслуживании (вероятность потери требования).
Отказ в обслуживании происходит, когда все каналы системы заняты, т.е. вероятность отказа в обслуживании равна вероятности того, что все каналы окажутся занятыми.
В качестве критерия эффективности СМО с ожиданием используют среднее время ожидания и среднюю длину очереди, а также вероятность того, что в системе в данный момент будет занято 0, 1, 2... и т.д. каналов.
В системах с ограниченным временем ожидания, кроме перечисленных, могут быть использованы и другие критерии. Например, в некоторых системах требование не может находиться больше заданного времени, т.е. оно покидает систему по истечении этого времени, независимо от того, начато его обслуживание или нет. Тогда частичное обслуживание требования относится к непроизводительным затратам. Если отношение этого времени функционирования системы велико, то обслуживание организованно плохо, эффективность системы низкая.
Важным критерием СМО является абсолютная и относительная пропускные способности.
Абсолютная пропускная способность характеризуется средним числом требований, которые система обслуживает в единицу времени. Относительная пропускная способность системы - отношение среднего числа обслуженных требований к числу поступивших в единицу времени.
В общем случае входной поток требований рассматривает как случайный процесс X(t). Для каждого значения t процесс представляет собой случайную величину.
В задачах теории массового обслуживания наиболее широкое распространение имеет входной поток, называемый пуассоновским потоком, обладающий свойствами ординарности и отсутствия последствия.
Ординарность потока требований означает, что вероятность появления двух и более требований в один и тот же момент времени равна нулю.
Практически в реальных потоках свойство ординарности означает, что вероятность одновременного появления двух и более требований пренебрежимо мала.
Отсутствие последствия заключается в том, что вероятность поступления на участок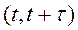 
определенного числа требований не зависит от того, сколько требований уже поступило в систему до момента t.
Отсутствие последействия предопределяет взаимную независимость протекания потока на неперекрывающихся отрезках времени.
Свойство отсутствия последствия возникает тогда, когда появление последовательных требований вызвано различными несвязанными друг с другом причинами.
Для пуассоновского потока вероятность поступления ровно m требований в заданном интервале 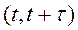определяется формулой Пуассона:
, (1)
где а - среднее число требований, поступающих в интервале .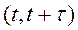
Важной характеристикой входного потока является его интенсивность, или плотность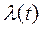 
. Интенсивность потока - называют математическое ожидание числа требований в единицу времени.
Если интенсивность пуассоновского потока 
, то такой поток требований называют стационарным пуассоновским или простейшим потоком.
Для простейшего потока:
, (2)
в любой момент времени t.
Если интенсивность потока есть функция времени, поток называют нестационарным, а среднее число требований в интервале 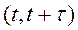выражается интегралом:
Заметим, что формула (1) справедлива для обоих случаев.
Для простейшего потока формула (1) с учетом равенства (2) при m=0 дает:
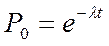
Это есть вероятность того, что в интервале 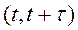не поступит ни одного требования. Вероятность противоположного события, поступления в интервале 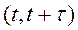хотя бы одного требования:
Время обслуживания одного требования (Tоб.) является случайной величиной, поэтому полной его характеристикой будет закон распределения:
,
т.е. вероятность того, что время обслуживания Тоб. не превысит некоторой величины t (обслуживание требований к моменту t закончено).
Наиболее простым законом распределения времени обслуживания, получившим большое распространение в задачах массового обслуживания, является показательный закон:
,
где 
- постоянная величина, обратная математическому ожиданию времени обслуживания одного требования, которая представляет собой интенсивность потока обслуженных требований, т.е. среднее число обслуженных требований в единицу времени.
Показательный закон характерен тем, что вероятность быстрого обслуживания системой достаточно велика.
Отметим весьма важное свойство показательного закона распределения времени обслуживания; закон распределения оставшейся части времени обслуживания не зависит от того, сколько времени обслуживание уже продолжалось. Математически это свойство запишется в виде:
,
где 
- вероятность того, что обслуживание, которое продолжалось уже время 
, продлится еще не меньше времени t.
Другое важное свойство показательного закона заключается в следующем. Если система обслуживания состоит из n независимых каналов и время обслуживания каждого i-го канала (i= 1,2,...) подчинено показательному закону с параметром 
, то закон распределения времени обслуживания системы в целом будет также показательным:
где 
.
Как показывают данные наблюдений, наиболее часто встречаются на практике системы, в которых поток требований близок к простейшему, а время обслуживания является показательным. Эти системы наиболее полно разработаны в теории массового обслуживания.
Основные типы СМО
